[算法系列之十四]字符串匹配之Morris-Pratt字符串搜索算法

前言

我们前面已经看到，蛮力字符串匹配算法和Rabin-Karp字符串匹配算法均非有效算法。不过，为了改进某种算法，首先需要详细理解其基本原理。我们已经知道，暴力字符串匹配的速度缓慢，并已尝试使用Rabin-Karp中的一个散列函数对其进行改进。问题是，Rabin-Karp的复杂度与强力字符串匹配相同，均为O(mn)。

我们显然需要采用一种不同方法，但为了提出这种不同方法，先来看看暴力字符串匹配有什么不妥之处。事实上，再深入地研究一下它的基本原理，就能找到问题的答案了。

在暴力匹配算法中，需要检查文本串中的每个字符是否与模式串的第一个字符匹配。如果匹配，就顺次比较模式串的第二个字符，判断是否与文本串的下一字符匹配。问题在于，当出现失配时，我们必须要在文本串中回退若干位置。嗯，这种方法事实上是无法优化的。

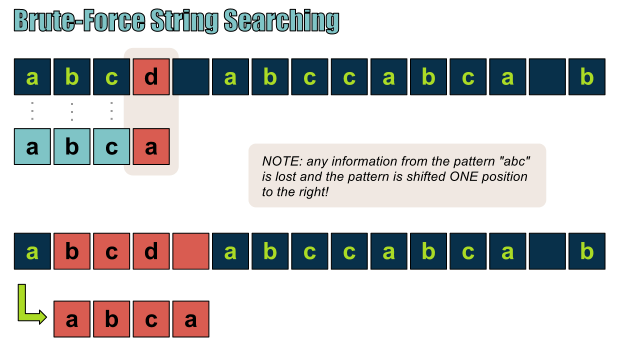
在暴力字符串匹配算法中，若出现失配，必须回退，并匹配已经匹配过的字符！

我们可以从上图可以看出问题所在：一旦出现失配，必须回退，从文本串中一个已经考察过的位置开始比较。在我们的例子中，我们已经检查了第一、二、三、四个字符，此时模式串与文本串之间出现失配，于是……于是我们就不得不得回退回去，从文本串的第二个字符重新开始比较。

这一过程显然没有任何作用，因为我们已经知道模式串从字符“a”起始，并且在位置1与位置3之间没有这一字符。那我们如何改善这种不必要的重复呢？

概述

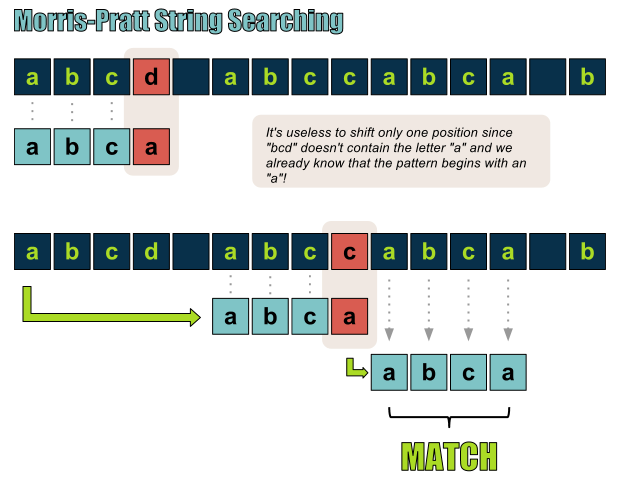
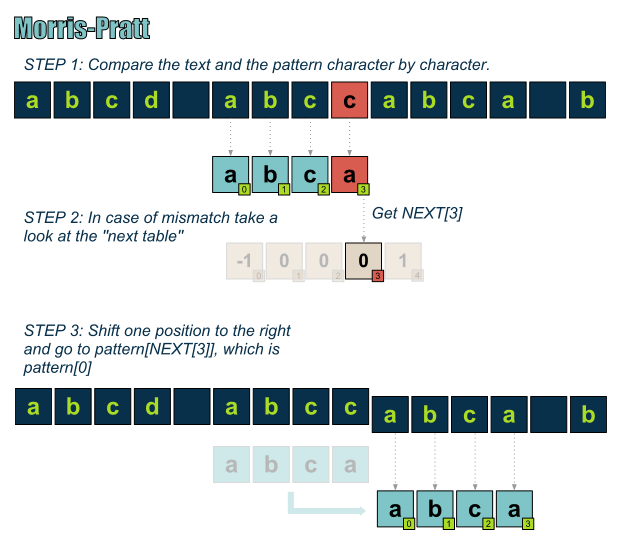
James H. Morris和Vaughan Pratt在1977年回答了这一问题，并且对自己的算法进行了介绍，这种算法会跳过大量无用比较，所以其效率高于暴力字符串匹配。我们来详细地研究一下。唯一事情就是：利用在对模式串与可能匹配进行对比期间收集的信息（The only thing is to use the information gathered during the comparisons of the pattern and a possible match），如下图所示。

Morris-Pratt向前移动到下一可能匹配位置，从而跳过一些不必要的比较！

我们首先需要做的就是必须对模式串进行预处理，以获取后续匹配的可能位置。下一步，开始查找可能的匹配位置，在发生失配的情况下，我们可以准确地知道应当跳转到何处，从而跳过那些没有任何用处的比较。

生成后续对比位置表格

这是Morris-Pratt算法中最富有技巧性的地方，也是这种算法如何克服暴力字符串匹配算法缺陷的重要步骤。让我们来看几张图片。

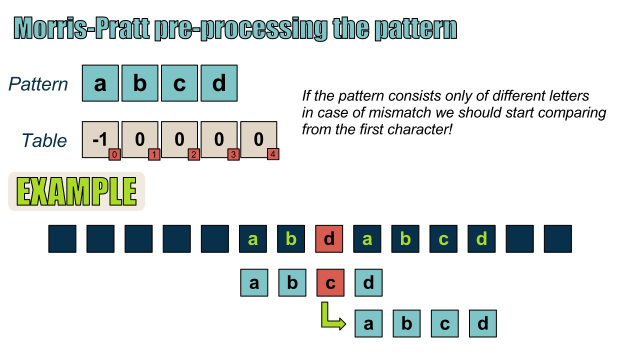
很显然，如果模式串中仅包含不同字符，在发生失配时，我们应当将文本串中的下一字符与模式串的第一字符进行比较！

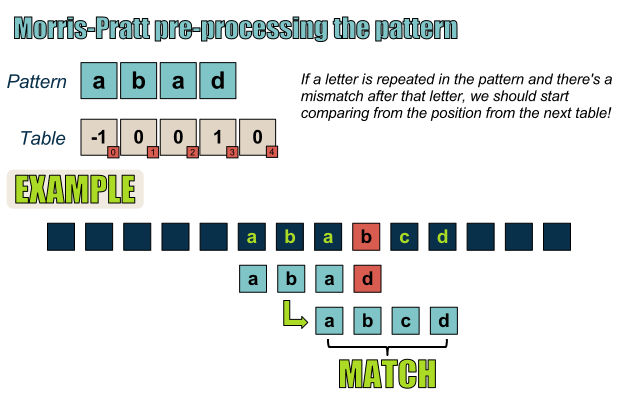
然而，当模式串中存在重复字符情况时，如果在该字符之后出现失配，则必须从这一重复字符开始查找可能的匹配，如下图所示。

如果模式串中包含重复字符，则“下一位置”表格会稍有不同！

最后，如果文本串中的重复字符不止1个，“下一个”表格将会给出其位置。

有了这个包含“后续”可能位置的表格之后，就可以开始在文本串中查找模式串了。

实现

Morris-Pratt算法的实现并不困难。首先，必须对模式串进行预处理，然后执行搜索。原文是使用PHP实现的，在这我们使用c++实现。

/*--------------------------------
*   日期：2015-02-05
*   作者：SJF0115
*   题目: 字符串匹配之Morris-Pratt匹配算法
*   博客：
------------------------------------*/
#include <iostream>
using namespace std;// 预处理
void PreprocessMorrisPratt(string patttern,int nextTable[]){int i = 0;int j = nextTable[0] = -1;int size = patttern.size();while(i < size){while(j > -1 && patttern[i] != patttern[j]){j = nextTable[j];}//whilenextTable[++i] = ++j;}//while
}int SubString(string text,string pattern){int m = pattern.size();int n = text.size();int nextTable[m+1];// 预处理PreprocessMorrisPratt(pattern,nextTable);int i = 0,j = 0;while( j < n){while(i > -1 && pattern[i] != text[j]){i = nextTable[i];}//whilei++;j++;if(i >= m){return j  - i;}//if}//whilereturn -1;
}int main(){string text("Lorem ipsum dolor sit amet, consectetur adipiscing elit. Quisque eleifend nisi viverra ipsum elementum porttitor quis at justo. Aliquam ligula felis, dignissim sit amet lobortis eget, lacinia ac augue. Quisque nec est elit, nec ultricies magna. Ut mi libero, dictum sit amet mollis non, aliquam et augue!");string pattern("mollis");int result = SubString(text,pattern);// 275cout<<"下标位置->"<<result<<endl;return 0;
}

复杂度

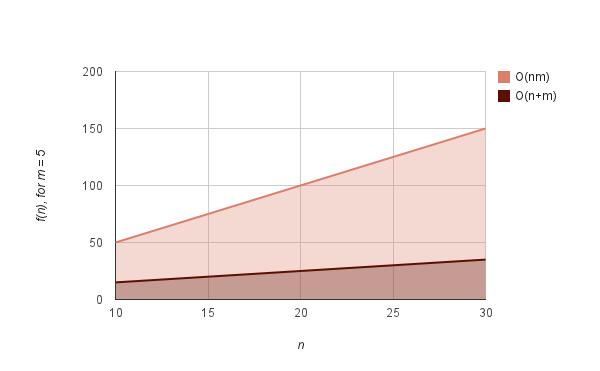
这一算法需要一定的时间和空间进行预处理。模式串的预处理可以在O(m)内完成，其中m为模式串的长度，而搜索本身需要O(m+n)。好消息是预处理过程只需要完成一次，然后就可以根据需要执行任意次搜索了！

下面的图表给出了5字母模式串的O(n+m)复杂度，并将其与O(nm)进行对比。

应用

优点

其搜索复杂度为O(m+n)，快于强力算法和Rabin-Karp算法 
其实现相当容易

缺点

需要额外的空间与时间-O(m)进行预处理 
可以稍加优化（Knuth-Morris-Pratt）

应用

优点

其搜索复杂度为O(m+n)，快于强力算法和Rabin-Karp算法 
其实现相当容易

缺点

需要额外的空间与时间-O(m)进行预处理 
可以稍加优化（Knuth-Morris-Pratt）

本文原文地址：https://blog.csdn.net/SunnyYoona/article/details/43560619