一篇优质的Knuth-Morris-Pratt算法讲解

部分匹配表

KMP的关键是部分匹配表。我和理解KMP之间的主要障碍是我没有完全理解部分匹配表中的值的真正含义。我现在将尽可能用最简单的话来解释它们。

下面是模式“ABABABACA”的部分匹配表：

如果我有一个八个字符的模式（在本例的持续时间内，让我们说“abababca”），我的部分匹配表将有八个单元格。如果我看表中的第八个也是最后一个单元格，我对整个模式感兴趣（“abababca”）。如果我看表中的第七个单元格，我只对模式中的前七个字符（“ababac”）感兴趣；第八个（“a”）是不相关的，可以从建筑物或其他东西上掉下来。如果我看到桌子上的第六个单元格，你会明白的。请注意，我还没有讨论每个单元格的含义，只是讨论了它所指的内容。
现在，为了讨论词义，我们需要知道正确的前缀和后缀。

正确前缀：字符串中的所有字符，末尾有一个或多个字符被截断。“S”、“Sn”、“Sna”和“Snap”都是“Snap”的正确前缀。

正确后缀：字符串中的所有字符，开头有一个或多个字符被截断。“agrid”、“grid”、“rid”、“id”和“d”都是“Hagrid”的适当后缀。

考虑到这一点，我现在可以给出部分匹配表中值的一句话含义：

（子）模式中与同一（子）模式中的正确后缀匹配的最长正确前缀的长度。

让我们来看看我的意思。假设我们在第三间牢房里。从上面你会记得，这意味着我们只对前三个字符（“aba”）感兴趣。在“aba”中，有两个适当的前缀（“a”和“ab”）和两个适当的后缀（“a”和“ba”）。正确的前缀“ab”与两个正确的后缀都不匹配。但是，正确的前缀“a”与正确的后缀“a”匹配。因此，在本例中，与正确后缀匹配的最长正确前缀的长度为1。

让我们在第四牢房试试。这里，我们对前四个字符（“abab”）感兴趣。我们有三个合适的前缀（“a”、“ab”和“aba”）和三个合适的后缀（“b”、“ab”和“bab”）。这一次，“ab”在两者中，有两个字符长，所以第四单元的值为2。

因为这是一个有趣的例子，让我们也在涉及“ababa”的第五单元中尝试一下。我们有四个适当的前缀（“a”、“ab”、“aba”和“abab”）和四个适当的后缀（“a”、“ba”、“aba”和“baba”）。现在，我们有两个匹配项：“a”和“aba”都是正确的前缀和后缀。因为“aba”比“a”长，所以它获胜，第五单元的值为3。

让我们跳到第七单元（倒数第二个单元），它与模式“ababac”有关。即使没有列举所有正确的前缀和后缀，也应该很明显不会有任何匹配项；所有后缀都将以字母“c”结尾，没有一个前缀将以字母“c”结尾。由于没有匹配项，第七单元得到0。

最后，让我们看看第八单元，它涉及整个模式（“阿巴巴卡”）。由于它们都以“a”开头和结尾，我们知道该值至少为1。然而，这就是它的终点；长度为2及以上时，所有后缀都包含c，而只有最后一个前缀（“ababac”）包含c。这个七个字符的前缀与七个字符的后缀（“bababca”）不匹配，所以第八单元得到1。

如何使用部分匹配表

当我们发现部分匹配时，可以使用部分匹配表中的值提前跳过（而不是重复不必要的旧比较）。公式的工作原理如下：

如果找到长度为partial_match_length的部分匹配，并且表[partial_match_length]>1，我们可以跳过partial_match_length-表[partial_match_length-1]字符。

假设我们将模式“abababca”与文本“bacbabab”进行匹配。这是我们的部分匹配表，便于参考：

我们第一次得到部分匹配是在这里：

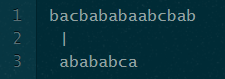
This is a partial_match_length of 1. The value at table[partial_match_length - 1] (or table[0]) is 0, so we don’t get to skip ahead any. The next partial match we get is here:

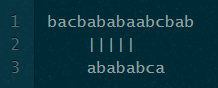
这是5的部分匹配长度。表[partial_match_length-1]（或表[4]）中的值为3。这意味着我们可以提前跳过部分匹配长度表[partial\u match\u length-1]（或5表[4]或5-3或2）字符：

这是3的部分匹配长度。表[partial_match_length-1]（或表[2]）中的值为1。这意味着我们可以提前跳过部分匹配长度表[部分匹配长度-1]（或3表[2]或3-1或2）字符：
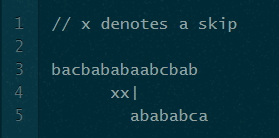此时，我们的模式比文本中的其余字符长，因此我们知道不存在匹配。