本文主要是介绍【leetcode系列】【算法】【中等】二叉树的中序遍历(递归,栈,莫里斯morris),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
题目:
解题思路:
方法一:递归(时间O(N),空间O(N))
方法二:栈(时间O(N),空间O(N))
方法三:莫里斯遍历(时间O(N),空间O(1))
解题思路:
方法一:递归
方法二:栈
方法三:莫里斯
题目:

题目链接: https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
解题思路:
方法一:递归(时间O(N),空间O(N))
每次递归,如果有左子树,就继续使用左子树继续递归
如果没有左子树,就将当前值加入到结果集中,返回到上一层递归中
在上一层递归中,先将当前值加入到结果集中,继续判断是否有右子树
如果有右子树,继续使用右子树递归,如果没有右子树,继续返回上一层递归,重复此逻辑
方法二:栈(时间O(N),空间O(N))
先将根节点入栈,开始遍历
只要栈不为空,就从栈中获取栈顶的元素,并判断是否有左子树
如果有左子树,将左子树入栈,然后继续遍历;下次遍历获取到的栈顶元素,为本次遍历入栈的左子树
如果没没有左子树,将当前值加入到结果集中,并将栈顶子树出栈
继续从栈顶获取子树,并将栈顶子树出栈,将值加入到结果集中,然后判断是否有右子树
如果有右子树,则将右子树出栈,继续大循环;如果没有右子树,则继续小循环,获取栈顶元素
图示如下:
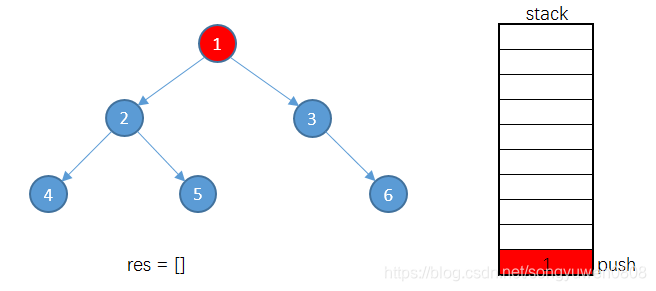
将根节点入栈
将1的左子树2入栈
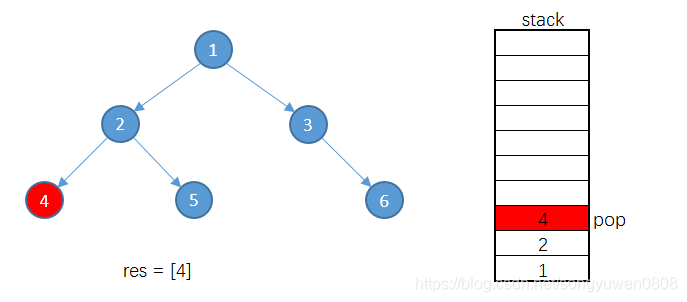
将2的左子树4入栈
因为4没有左子树,将4出栈,并将4加入到结果集res中
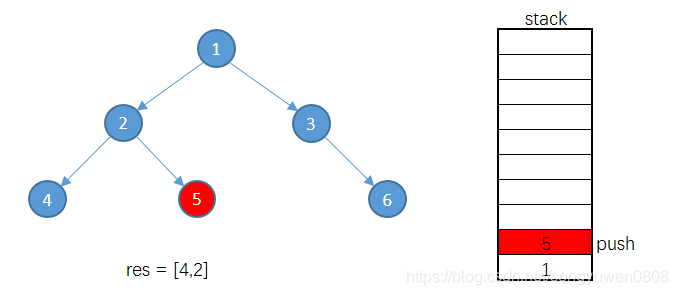
因为4没有右子树,所以继续将栈顶元素2出栈,并加入到结果集res中
因为2有右子树,所以不继续从栈顶获取元素,而将2的右子树5入栈
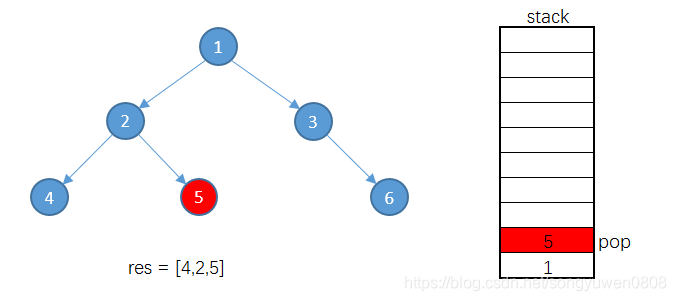
5的情况与4相同,将5出栈,加入到结果集中
从栈顶将1出栈,加入到结果集中
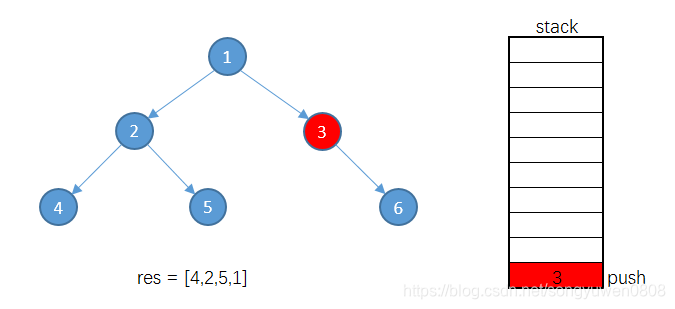
因为1有右子树,所以将1的右子树3入栈
因为3没有左子树,将栈顶元素3出栈,加入到结果集
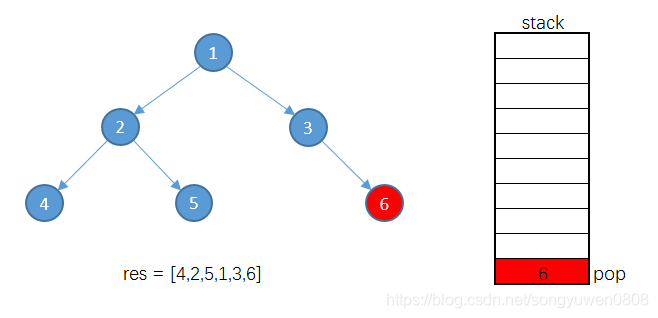
将3的右子树入栈
将6出栈,加入到结果集中
栈中没有元素,停止遍历,返回结果
方法三:莫里斯遍历(时间O(N),空间O(1))
逻辑大致如下:
变量:
- root:树的根节点
- curr:当前遍历到的节点,初始化为root
- prev:辅助节点,初始化为空
流程:
- 如果curr左子树为空,则将curr值加入到结果集中,并开始遍历curr的右子树
- 如果curr左子树不为空,则进行下记操作:
- prev从curr左子树的右子树开始遍历,直到没有右子树,或者遍历到curr节点
- 如果prev右子树为空,则将prev右子树指向curr
- 如果prev右子树不为空,则将curr.val加入到结果集,更新curr = curr.right右子树,prev = None,继续遍历
图示:
假设一个树原始结构如下:
黑色节点永远为原始root节点,此时将curr指向root节点,curr节点左子树为2,不为空,此时将prev指向2,开始从2的右子树5遍历:
当搜索到8时,因为8没有右子树,停止搜索,此时三个节点情况如下(curr、root都在1位置):
此时,将prev的右子树指向curr,更新curr = curr.left,此时的节点位置和连接情况如下(实线为原始树结构,虚线为新加的连接):
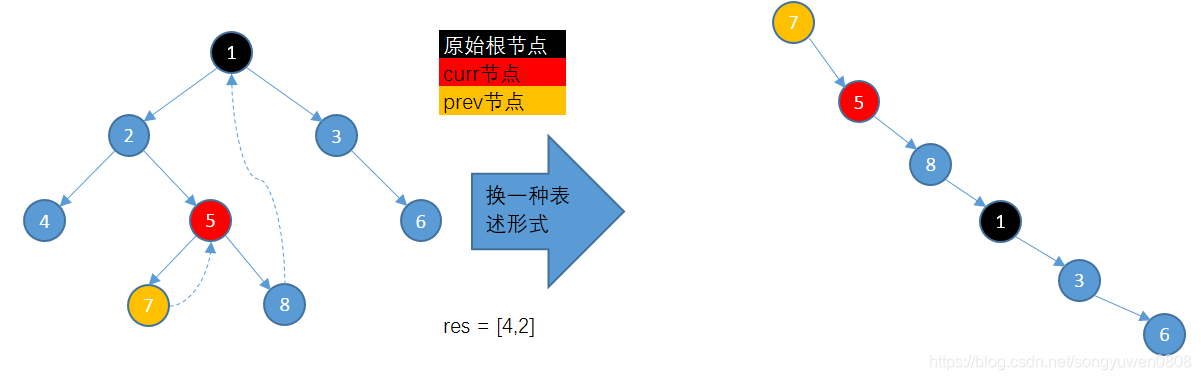
继续循环,此时prev = 2的左子树不为空,继续将prev指向curr的左子树,开始搜索:
4没有右子树,所以直接退出搜索,继续将prev的右子树指向curr,更新curr = curr.left,此时节点位置和链接情况如下(因为prev指向4后,没有向右子树遍历,所以此时prev和curr在同一位置):
此时继续遍历时,发现curr没有左子树,所以将curr的值加入到结果集res中,通过虚线,更新curr = curr.right,开始下次循环。此时curr = 2,所以prev = curr.left继续从2的左子树4开始搜索,4的右节点为2,符合了curr = prev的条件,搜索停止,此时情况如下:
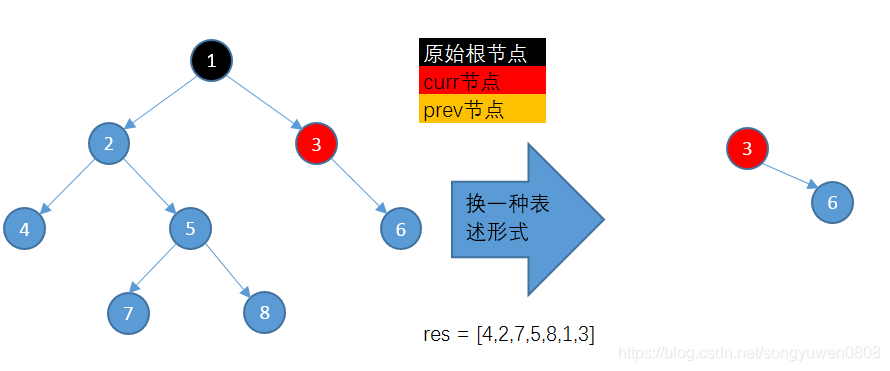
搜索停止时,prev = 4的右子树不为空,所以此时将2加入到结果集中,更新curr = curr.right,删除掉之前多添加出来的连接,即更新prev.right = None,继续循环:
之后逻辑与上述相同,图示流程如下:
解题思路:
方法一:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:def order_help(node, res):if node and node.left:order_help(node.left, res)if node:res.append(node.val)if node and node.right:order_help(node.right, res)res = []order_help(root, res)return res
方法二:栈
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:if not root:return []node_stack = [root]res = []while 0 < len(node_stack):if node_stack[-1].left:node_stack.append(node_stack[-1].left)continuewhile 0 < len(node_stack):last_node = node_stack[-1]node_stack.pop()res.append(last_node.val)if last_node.right:node_stack.append(last_node.right)breakreturn res
方法三:莫里斯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:curr = rootprev = Noneres = []while curr:if not curr.left:res.append(curr.val)curr = curr.rightelse:prev = curr.leftwhile prev.right and prev.right != curr:prev = prev.rightif not prev.right:prev.right = currcurr = curr.leftelse:res.append(curr.val)prev.right = Nonecurr = curr.rightreturn res
这篇关于【leetcode系列】【算法】【中等】二叉树的中序遍历(递归,栈,莫里斯morris)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!