KMP 算法(Knuth–Morris–Pratt algorithm)的基本思想

KMP 算法(Knuth–Morris–Pratt algorithm)的基本思想

阅读本文之前，您最好能够了解 KMP 算法解决的是什么问题，最好能用暴力方式（Brute Force）解决一下该问题。
KMP 算法主要想解决的是文本搜索的问题: 给定一个模式字符串 p 和一个子串 t， 找出 p 串出现在 t 串中的位置。

术语定义

• 
  
• "abc"(引号中的字符串): 代表字符串字面值
• a…z(单个斜体小写字母): 代表字符串。
• A…Z(单个大写字母)：代表单个字符。
• prefix(x, n): 字符串 x 的前 n 个字符构成的子串(前缀)。
• suffix(x, n): 字符串 x 的后 n 个字符构成的子串(后缀)。
• |a|: 字符串 a 的长度。
  

如: 字符串 x = "abcdef", 则 prefix( x, 3) = "abc", suffix( x, 3) = "def"，| x| = 6。

KMP 算法的基本思想

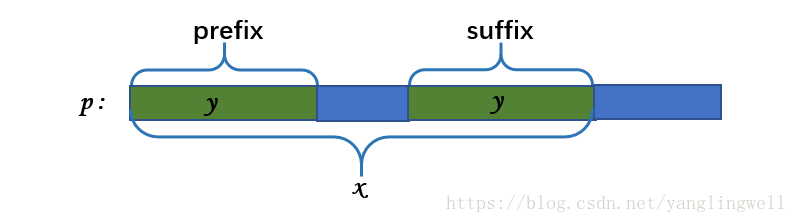
假设字符串 x = prefix(p, n)，且存在 i > 0 使得字符串 y := prefix(x, i) := suffix(x, i),
则p, x 和 y 之间的关系如下图:

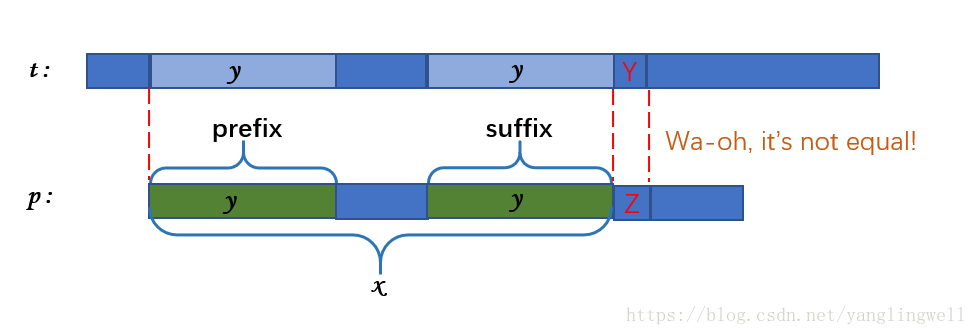
若 t 串匹配到 p 串的前缀x，并且在 x 串的下一个串匹配失败，如下图:

仔细观察上图可以发现，此次匹配失败后，我们不用按照暴力算法直接将 p 串移动一位，从头开始比较。
而是将 prefix(x, i) 移动到 suffix(x, i) 的位置，继续比较第 |y|+1 位。
这是因为此时已经匹配成功的 p 串和 x 串(即, prefix(t,n)) 相等。
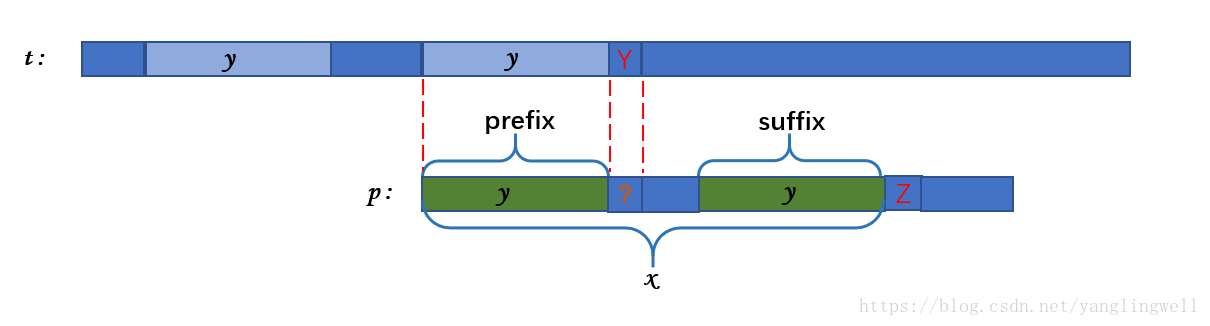
结合下图(移动后的情况)，仔细理解上一句话:

以上，就是 KMP 算法的最核心思想。我们不难发现，i 越大，移动之后匹配成功的字符就越多, 并且只有 i 取得最大值时， 才不会移动过多的位。
因此，KMP 算法找的是使得 prefix(p, i) == suffix(p, i) 最大的 i, 记作 i_max, 此时的 y 串记作 y _max。

容易求得，每次移动的位数是 |x| - | y _max|。
将 prefix(p, 1…|p|) (即 p 串的所有前缀 ) 的 i_max 打成一个表格，就是 KMP 算法所谓的 next 数组。