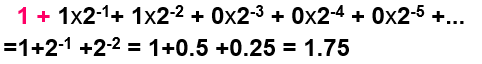怎么用二进制来表示小数呢？ 假设我们要用二进制来表示小数5.5，怎么搞？ 按照常规思路，首先用二进制表示一下5，是101，那5.5岂不就是101.101(呵呵哒...)。 我们来看下分解过程，5=4+1，也就是1*2 2 + 0*2 1 + 1*2 0，即101。按照这个思路，0.101这个二进制表示的是1*2 -1 + 0*2 -2 + 1*2 -3，也就是0.625。

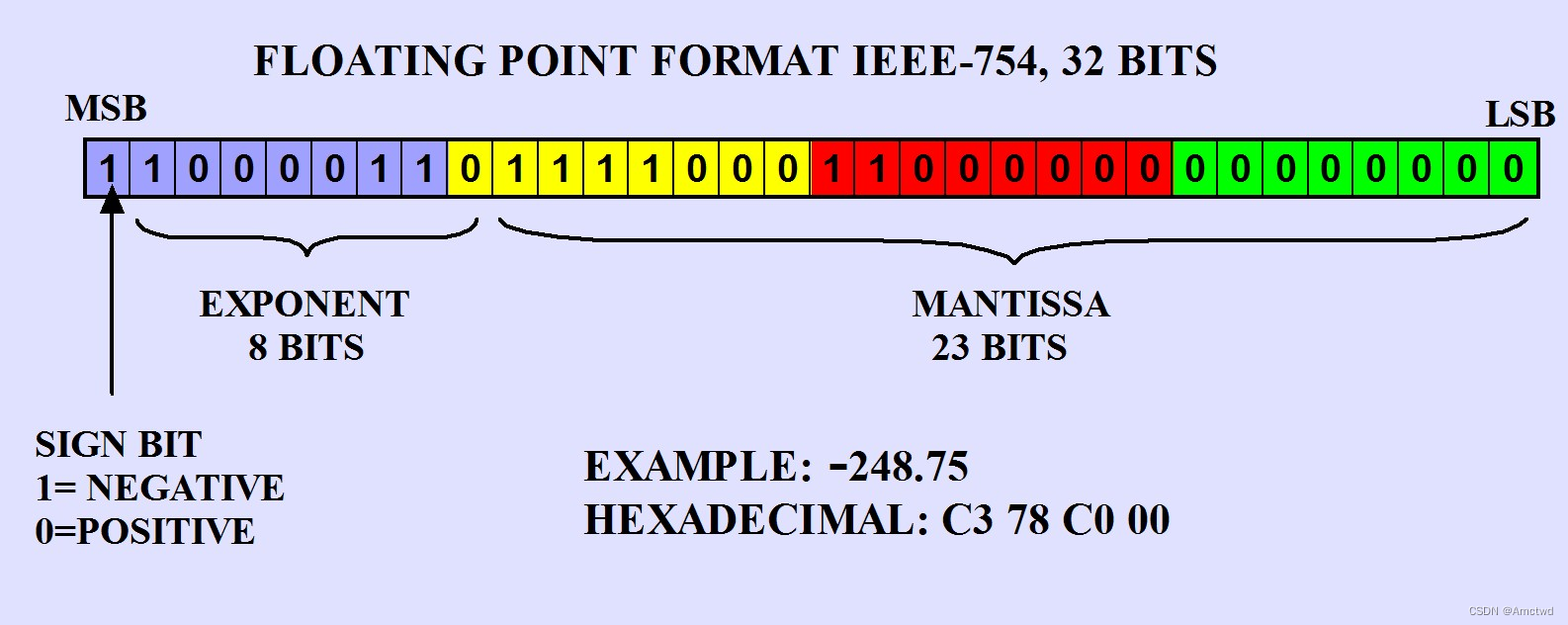
IEEE754介绍   IEEE 754是一种标准，用于表示和执行浮点数运算的方法。在这个标准中，单精度浮点数使用32位二进制表示，分为三个部分：符号位、指数位和尾数位。 符号位(s)用一个位来表示数的正负，0表示正数，1表示负数。 指数位(e)用8位表示指数。对于单精度浮点数，指数位是以偏移量的形式表示的。也就是说，实际的指数值是指数位的无符号值减去一个偏移量（127）。 尾数位(m)用

2019独角兽企业重金招聘Python工程师标准>>> 　　昨晚，科协的群里提到了移码，相对陌生的词汇，我从未见过，后来搜索了下资料，发现了IEEE754中采用的是127（32bit），很是疑惑，一般不都是128吗？ 　　经过计算发现了一个现象，只能说这个相当巧妙！ ————————————————————————————————————————————————————— 1.   首

IEEE754是现在公认的、最广泛使用的浮点数转换运算标准，为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number）），一些特殊数值（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。       IEEE 754规定了四种表示浮

1. IEEE754 标准简介 IEEE754 标准是一种用于浮点数表示和运算的标准，由国际电工委员会（IEEE）制定。它定义了浮点数的编码格式、舍入规则以及基本的算术运算规则，旨在提供一种可移植性和一致性的方式来表示和处理浮点数 IEEE754 标准定义了两种常见的浮点数格式：单精度（32位）和双精度（64位）。这些格式使用了符号、阶码（指数）、尾数的二进制表示形式，其中符号表示浮点数的正负，

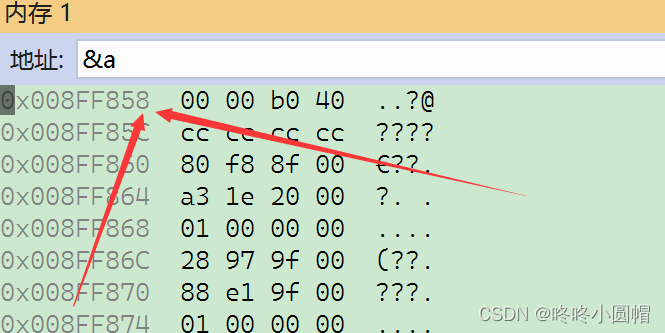
作者的话 本文涵盖了浮点型在内存中的如何存储、如何取出、为何有精度丢失等知识点~ 浮点型概括 常见的浮点型数据有三种： 以科学计数法表示的：1e10、1.28e10数据后加入字符‘f’的：3.14f、7.76f不用科学计数法也不加f：1.22、4.89 第一种表示： 1＊10^10　和　1.28＊10^10 第二种表示： 用float创建的浮点数，要在后面加’f’，不然会默认为dou

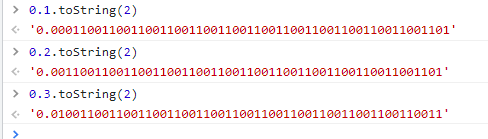
本人是一个web前端开发工程师，主要是vue框架，整理了一些面试题，今后也会一直更新，有好题目的同学欢迎评论区分享 ;-） web面试题专栏：点击此处 背景 WEB前端面试官：0.2+0.3是否等于0.5？ ：） 好家伙，不按套路出牌，之前也没深究，但是既然重新学习一下，就记录一下，免得又忘记了。 分析问题 面试官是问你0.1+0.2，或者0.2+0.3的问题吗？ 不是的，要是

IEEE754-2008 标准详解(一)：浮点数据的分类 本文为原创文章，转载请注明出处，并注明转载自“黄邦勇帅(原名：黄勇)” 本文是对《C++语法详解》一书相关章节的增补，以增强读者对浮点数的理解，原书引用的是老版的 IEEE754-1985 标准 《C++语法详解》网盘地址：https://pan.baidu.com/s/1dIxLMN5b91zpJN2sZv1MNg 本文摘自本人所作

http://zh.wikipedia.org/wiki/IEEE_754 IEEE二进制浮点数算术标准（IEEE 754）是1980年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number）），一些特殊数值（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四

目录 EEE754 32位浮点数的结构 这是将-1313.3125转换为IEEE 32位浮点格式的规则 单精度二进制浮点数存储在一个32位的字中: 在这种格式中，初始位没有被抑制，基数点被设置在尾数的左边，以4位为单位递增。 由于基数是16，所以这种形式的指数大约是IEEE 754中相同指数的两倍，为了在二进制中有相似的指数范围，需要9个指数位。 Example 考虑将值-