本文主要是介绍web前端面试-- IEEE754标准JS精度丢失问题0.1+0.2!=0.3、0.2+0.3==0.5 十进制转二进制讲解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本人是一个web前端开发工程师,主要是vue框架,整理了一些面试题,今后也会一直更新,有好题目的同学欢迎评论区分享 ;-)
web面试题专栏:点击此处

背景
WEB前端面试官:0.2+0.3是否等于0.5?
:)
好家伙,不按套路出牌,之前也没深究,但是既然重新学习一下,就记录一下,免得又忘记了。
分析问题
面试官是问你0.1+0.2,或者0.2+0.3的问题吗?
不是的,要是下次有个作妖的问你,0.x+0.y呢?
显然不是,他要问你的是原理~
0.1+0.2
// 0.30000000000000004
0.2+0.3
// 0.5
控制台运行如下:
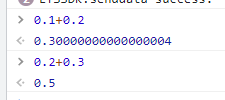
原理
死记硬背~~~。
- 在浏览器的JavaScript环境中,遵循IEEE 754标准,就算记不全,也要记得IEEE(理科生搞得跟文科生一样,真蛋疼。。。)
- 这个标准规定了浮点数的二进制表示以及浮点数的运算规则。
- JavaScript中的Number类型就是基于这个标准实现的。因此,JavaScript中的浮点数遵循IEEE 754标准的规定,也会出现浮点数精度问题。
总的来说:IEEE754标准下,浮点数是用二进制进行存储运算的,部分十进制小数转成二进制是一个无限循环的数值,运算的时候会造成精度丢失。
复现
在浏览器环境中以IEEE754存储的0.1、0.2、0.3 咱们可以直接在控制台打印出来。
0.1.toString(2);
0.2.toString(2);
0.3.toString(2);
控制台运行如下:
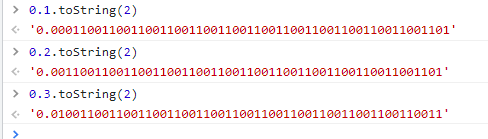
十进制小数转二进制
方法:小数乘2取整,直到没有小数为空,最后取整的数值进行正向排列就得到了。
以0.1 为例:
| 数值 | 取整 |
|---|---|
| 0.1 * 2 = 0.2 | 0 |
| 0.2 * 2 = 0.4 | 0 |
| 0.4 * 2 = 0.8 | 0 |
| 0.8 * 2 = 1.6 | 1 |
| 0.6 * 2 = 1.2 | 1 |
| 0.2 * 2 = 0.4 | 0 |
| 0.4 * 2 = 0.8 | 0 |
| 0.8 * 2 = 1.6 | 1 |
| 0.6 * 2 = 1.2 | 1 |
| 0.2 * 2 = 0.4 | 0 |
| 0.4 * 2 = 0.8 | 0 |
| 0.8 * 2 = 1.6 | 1 |
| 0.6 * 2 = 1.2 | 1 |
| (无限循环)… | … |
正向排列整理后: 0001100110011…
十进制证书转二进制
方法:整数除2取余,直到整数为0,最后取余的数值进行倒叙排列就得到了。
以6为例:
| 数值 | 余数 |
|---|---|
| 6 / 2= 3 % 0 | 0 |
| 3 / 2 = 1 % 1 | 1 |
| 1 / 2 = 0 % 1 | 1 |
倒叙排列整理后: 110
这篇关于web前端面试-- IEEE754标准JS精度丢失问题0.1+0.2!=0.3、0.2+0.3==0.5 十进制转二进制讲解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




