IEEE754-2008 标准详解(一)：浮点数据的分类

本文主要是介绍IEEE754-2008 标准详解(一)：浮点数据的分类，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

IEEE754-2008 标准详解(一)：浮点数据的分类

本文为原创文章，转载请注明出处，并注明转载自“黄邦勇帅(原名：黄勇)”
本文是对《C++语法详解》一书相关章节的增补，以增强读者对浮点数的理解，原书引用的是老版的 IEEE754-1985 标准

《C++语法详解》网盘地址：https://pan.baidu.com/s/1dIxLMN5b91zpJN2sZv1MNg

本文摘自本人所作《IEEE754-2008标准详解》网盘地址
链接：https://pan.baidu.com/s/10soDctgCJ84MDs3PyhJBcw?pwd=lzku
提取码：lzku

有兴趣的读者可参阅本人所著《C++语法详解》一书，电子工业出版社出版，该书语法示例短小精悍，对查阅C++知识点相当方便，并对语法原理进行了透彻、深入详细的讲解，可确保读者彻底弄懂C++的原理，彻底解惑C++，使其知其然更知其所以然。此书是一本全面了解C++不可多得的案头必备图书。

由于本人能力有限，文中难免有错漏之处，望广大读者指出更正，不胜感激

第1章 IEEE 754-2008对浮点数据的分类及基本概念

1、注：本文将IEEE 754 -2008简称为IEEE 754
2、实现：比如，想造一辆汽车，于是设计了方案A，然后根据方案A造出了汽车M，则汽车M就是方案A的实现，也可以说，汽车M实现了方案A。同理，IEEE754-2008只是一个现论上的标准(类似于方案A)，要使标准能真正成为现实，必须得有根据IEEE754标准的实现，通常编译器会实现IEEE754-2008中的标准，但不一定会实现所有标准。

1.1 格式

1、格式(format)：数值(numerical values)和符号的表示法(representations)的集合，可能伴有编码。

2、在IEEE中有如下几种类型的格式

1)、浮点格式：用于表示实数的有限子集
2)、算术格式(arithmetic format)：一种浮点格式，可用于表示IEEE754标准中的运算的浮点操作数或结果，IEEE754中的所有格式都支持算术格式。算术格式说明了以下几点内容：
- 算术格式是浮点格式的子集
- 不能用于本标准运算的浮点操作数或结果的格式则不是算术格式
- 算术格式的主要目的是用于参与计算，因此，这种格式不一定含有编码。
3)、整数格式：IEEE754标准中未定义的一种格式，表示整数的子集，也可能是表示无穷大、NaN或负零的附加值(additional value)。
4)、交换格式(interchange format)：在IEEE754标准中定义的具有特定的(specific)固定宽度编码的格式。交换格式由它们的大小标识，可以用于实现之间交换浮点数据。可把交换格式理解为是一种编码后的格式。
5)、基本格式：指的是以下五种格式
- 三种二进制格式，编码长度分别为32位、64位和128位。
- 两种十进制格式，编码长度分别为64位和128位。
  在任何一致性的(conforming)实现中都实现了一种或多种基本格式，但是具体使用的是哪一种基本格式，则是由语言定义的。

3、五种基本格式可以被实现为受支持的交换格式或算术格式(见图XXX)，若实现为交换格式则分别称其为二进制交换格式和十进制交换格式。
在这里插入图片描述

4、格式可理解为类型，因为编程语言如C++等，可通过类型来实现格式，如浮点格式可使用float、double等类型来实现。因此

浮点格式可理解为浮点类型
算术格式可理解为算术类型
整数格式可理解为整数类型
但，交换格式和基本格式应理解为编码后的格式

1.2 实数、浮点数、浮点数据

1、实数包括有理数和无理数，其中无理数是指无限不循环小数，如π，√2等。

2、由于计算机的存储容量有限，无限不循环小数、长度超过规定的有限小数都无法存储，因此，计算机处理的都是长度有限的实数，这些数被称为浮点数，所以，浮点数和实数是不同的，可把浮点数理解为是实数的近似，是实数的有限子集，浮点数通常在计算机中用于近似的表示任意某个实数。

3、浮点数的小数点在使用科学表示法(也称为指数表示法)时，可根据指数的不同而浮动，这是之所以被称为浮点数的原因。

4、由于浮点数是实数的近似，因此，浮点算术也是实算术的一种近似计算，因此，实算术的某些性质并不适用于浮点算术，如加法结合律。

5、在IEEE754-2008中的浮点数是指的除了NaN之外的浮点数据，而浮点数据包括，

1)、有符号0
2)、有限非零数，又分为
- 规约浮点数(normal floating-point number)，简称规约数
- 非规约浮点数(subnormal floating-point number)，简称非规约数
3)、有符号无穷大
4)、NaN (not-a-number，即，不是一个数)，又分为
- quiet NaN，简称为qNaN
- signaling NaN，简称为sNaN

6、需要注意的是，IEEE754中的0和无穷大都是有符号的。

1.3 浮点数据表示法及其值

1、IEEE 754-2008使用浮点数据表示法来表示浮点数据，使用浮点数据表示法表示的数是未编码的，浮点数据表示法包括以下内容：

使用如下形式的三元组表示的浮点数：

(sign, exponent, significand) //三元组表示法，公式1.1

表示的浮点数是

(−1) ^sign× b^exponent× significand //浮点数的指数表示法，公式1.2
其中b是基数，
sign是符号位，
exponent是指数，
significand是有效数，可表示有限非零浮点数及有符号0。
公式2被称为指数表示法或科学表示法，本文尽量不使用三元组表示法，而使用指数表示法。
+∞, −∞
qNaN (quiet NaN), sNaN (signaling NaN)

2、浮点数据表示法与其所表示的值的区别

在IEEE 754中浮点数据表示法与其所表示的值是两个不同的概念，如，假设sign =1，exponent = 5，significand = 2.34，基数b = 10，则以下三元组是IEEE 754的浮点数据表示法

	 (1, 5, 2.34)				//IEEE754浮点数据表示法

而以下形式表示的是浮点数据表示法的值

(−1)¹× 10⁵× 2.34 //浮点数据表示法的值

3、在IEEE 754中，NaN是浮点数据表示法的值，而qNaN或sNaN是浮点数据表示法

4、注意：本文不对“表示法”及其表示的值做严格的区分

5、图XXX是浮点数据的分类以及其表示法的总结

在这里插入图片描述

1.4 浮点格式表示的浮点数据范围

1、由于每一种格式的编码长度是有限的，这意味着，格式能表示的浮点数据的范围也是有限的，在特定格式中能表示的浮点数据的范围由基数、有效数的位数、指数的取值范围等限定。

2、IEEE754-2008规定，每种格式都必须能表示以下浮点数据：

1)、形式为以下情形的有符号零和有限非零浮点数

(−1)^s × m × b^e //公式1.3，用于表示二进制浮点数

或

(−1)^s × c × b^q //公式1.4，用于表示十进制浮点数

其参数见下文
2)、两个无穷大：+∞ 和−∞
3)、两个NaN：qNan和sNaN

3、公式3和公式4是公式2的一种简化形式，二者是等效的，可相互转换。使用两种形式表示法的主要目的在于在将浮点数进行编码时，使用不同的表示方法可以更方便的进行编码。二者的区别在于

公式3中的m是小数形式，指数使用e，公式4中的c是整数形式，指数使用q。因此，在本文之后，若遇到e或m时，指的是公式3的形式；遇到q或c时，指的是公式4的形式。
公式3通常用于表示二进制浮点数，二进制交换格式编码时通常使用该公式；公式4用于表示十进制浮点数，十进制交换格式编码时通常使用该公式。

4、公式3和公式4各参数意义如下：

1)、b为基数，其值为2或10
2)、s是符号位，其值为0或1，由公式可见，s为1表示负数，为0表示正数
3)、有效数
- m是形式为d₀.d₁ d₂…d_p−1的有效数(significand)，也被称为尾数，c是将有效数视为整数的情形，因此，c的形式为d₀ d₁ d₂…d_p−1 ，其中
  - p是有效数的位数(即精度)，p的取值见表XXX，需要注意的是，p是指的编码前的浮点数据有效数的位数。有关精度的讲解见后文
  - d_i为位于0≤d_i < b之间的整数，因此m和c分别是位于0≤m<b和0≤c<b^p间的整数
  - m的整数部分d0称为前导有效数(leading significand )。
  - m的小数部分d₁ d₂…d_p−1 ，称为末尾有效数(trailing significand)
- 这里的有效数可能与某些教材上使用的有效数有点区别，如1500 × 10³ 在IEEE754中，其有效数为1500，而在其他地方有可能有效数则是指的15。因此，本文尽量使用尾数一词，以避免产生不必要的理解混乱。注：IEEE754-2008不再使用尾数，而只使用有效数。
- 注意：尾数m或c是没有符号的(因为符号是由s指定的)，也就是说尾数总是一个正数。
4)、e和q是指数，其值是分别为位于

emin ≤ e ≤ emax //公式1.5
和
emin ≤ q+p − 1 ≤ emax //公式1.6

间的任何整数，其中，emax 是最大指数，emin是最小指数，且
```
  emin = 1−emax						//==公式1.7==
```
5)、可见，对于有限浮点数，公式3和公式4的关系如下

e = q+p − 1 //公式1.8
m = c × b^1−p //公式1.9

6、图XXX为指数表示法的图示
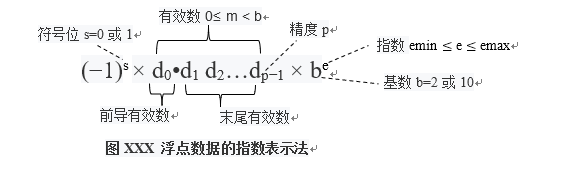
在这里插入图片描述
7、注意：公式3和公式4表示的是编码之前的真实值，其参数e、q、c、m、p、emin、emax等都是编码之前的真实参数。表XXX列出了p和emax的取值范围

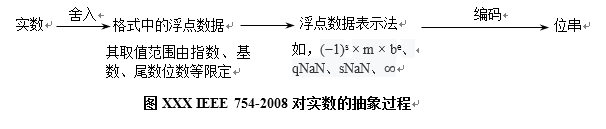
8、实数、浮点数据、浮点数据表示法、编码之间的关系
IEEE754将实数转换为二进制位串的过程：IEEE754通过舍入过程将实数映射为格式中包含的浮点数据，然后再将浮点数据映射到格式中的一种或多种浮点数据表示法，然后再通过编码将浮点数据表示法表示的浮点数据映射为位串。

在这里插入图片描述

1.5 规约数与非规约数

1、在特定格式中能表示的浮点数据的范围由基数、有效数的位数、指数的取值范围等限定。

2、以(−1)^s × m × b^e 为例，由于

m = d₀.d₁ d₂…d_p−1

1)、注意：尾数必须转换为与m的形式相同，即必须将尾数转换为纯小数形式，且最高位必须只有一位数
2)、因此，该公式能表示的最小的正数是

0.00…01 × b ^emin = b ^1−p× b ^emin =b ^emin+1−p //最小的正数，公式1.10

最大的正数是

(b−1).(b−1)(b−1)…(b−1) × b^emax = (b−b^1−p) × b ^emax //最大的正数，公式1.11
注1：以上的尾数位数总共有p位。
注2：为方便讲解，本小节使用“(b−x).(b−y)…(b−z)”的形式表示某个数，比如，若b =10，则(b−2).(b−3)(b−1) = 8.79
3)、比如，若b =2，则最小的正数是
0.00…01 × 2 ^emin = 2 ^1−p × 2 ^emin = 2 ^emin+1−p
最大的正数是
(2−1).(2−1)(2−1)…(2−1) × 2^emax =1.11…11 × 2^emax = (2 −2^1−p) × 2^emax
注：以上的尾数位数总共有p位。

3、IEEE754将以上所表示的浮点数据再次化分为规约数和非规约数。

需要注意的是，本文对规约数与非规约数的推导，其尾数是纯小数形式，而不是纯整数形式，也就是说，是以公式(−1)^s × m × b^e 为准来推导的，而不是以公式 (−1)^s × c × b^q 来推导的

4、规约数及其范围

IEEE754规定，最小的正规约数是

b ^emin //最小的正规约数，公式1.12
最大的正规约数就是最大的正数，即

(b−b^1−p) × b ^emax //最大的正规约数，公式1.13
由此可见，正规约数的范围位于最小正规约数与最大正数之间(含两端的值)，即

b ^emin ≤ 正规约数 ≤ (b−b^1−p) × b ^emax //正规约数的范围，公式1.14
同理，可得出负规约数的范围

−(b−b^1−p) × b ^emax ≤ 负规约数≤ −b ^emin //负规约数的范围，公式1.15

5、非规约数及其范围

1)、正非规约数的范围位于最小正数(含该值)与最小正规约数之间(不含该值)。即

b ^emin+1−p ≤ 正非规约数 < b ^emin

同理，可得出负非规约数的取值范围为

−b ^emin < 正非规约数 ≤ −b ^emin+1−p
2)、正负非规约数的取值范围通常使用以下公式(即，两端的不等式都含有等于)：

b ^emin+1−p ≤ 正非规约数 ≤ (1−b^1−p) × b ^emin //正非规约数的范围，公式16

−(1−b^1−p) ×b ^emin≤负非规约数≤ −b ^emin+1−p //负非规约数的范围，公式17
3)、公式14的推导过程，由于

b ^emin = 1.00…00× b ^emin (共p位尾数)
因此，最近的比 b ^emin小的数为(即，最大的正非规约数)
(1.00…00 − 0.00…01) × b ^emin (尾数长度均为p位)
= (1−b^1−p) × b ^emin
最小的正非规约数是
0.00.001× b ^emin = b ^1−p × b ^emin = b ^emin+1−p (共p位尾数)

6、规约数的判断方法

由于正规约数的取值范围为

b ^emin = 1.00…00× b ^emin (共p位尾数)
(b−b^1−p) × b ^emax = (b−1).(b−1)(b−1)…(b−1) × b^emax (共p位尾数)

从而可以推得，规约数必须同时满足以下两个条件(负规约数可推得相同的结论)

规约数的尾数大于等于1小于b (注意，尾数没有符号)，或者说，规约数的尾数的最高位一定只有一位 (即d₀)，且d₀大于等于1小于b，即

1 ≤ m < b (尾数大于等于1)

或

1 ≤ d₀ < b (最高有效位大于等于1)
并且指数的范围为：

emin ≤ e ≤ emax

7、非规约数的判断方法

由于正非规约数的取值范围为

(1−b^1−p) × b ^emin = 0.(b−1)(b−1)…(b−1) × b ^emin
b ^emin+1−p = 0.00.001× b ^emin

从而可以推得，非规约数必须同时满足以下两个条件(负非规约数可推得相同的结论)

非规约数的指数e恒为emin，是一个固定值，即，

e ≡ emin //非规约数的指数恒为emin，注：“≡”表示恒等于
并且，非规约数的尾数m小于1 (注意，尾数没有符号)，也就是最高有效位d₀ = 0，即

m < 1 //非规约数的尾数小于1

或

d₀ = 0 //非规约数的最高有效位为0

8、注意：以上公式的参数取值取决于具体使用哪种编码方式，编码方式不同，其参数的值不同，所表示的规约数与非规约数范围就不相同。

9、表XXX为规约数与非规约数的总结

在这里插入图片描述

10、示例：对于计算机中常使用的float型浮点数，若使用二进制交换格式编码(详见后文)时，各参数取值如下：

b = 2，p = 24，emin = −126，emax = 127

由此可计算出，最小的正规约数为

b ^emin = 2⁻¹²⁶ ≈1.1754943508 ×10^-38

最大的正规约数为

(b−b^1−p) × b ^emax= (2−2¹⁻²⁴) × 2 ¹²⁷ ≈ 3.402823 ×10^-38

最小的正非规约数为

b ^emin+1−p = 2^−126 + 1−24^ =2⁻¹⁴⁹ ≈ 1.4012985 ×10^-45

最大的正非规约数为

(1−b^1−p) × b ^emin = (1−2¹⁻²⁴) × 2 ⁻¹²⁶ ≈1.1754942107 ×10^-38

同理，可计算机负规约数与负非规约数的取值范围

通过以上计算可以看到，最小正规约数与最大正非规约数的大小是非常接近的。

float型浮点数二进制交换格式编码时的规约数和非规约数的范围如下表XXX所示

在这里插入图片描述

11、非规约数与规约数的区别

以下讲解均是指的正规约数和正非规约数，负数可根据以下规则同理推出

由前文讲解可知

IEEE 754可以表示0，但并不能表示“0到最小规约数”之间的所有数，即使使用非规约数，也最小只能表示到与0更接近的“最小的非规约数”。所以，对于float型二进制交换格式编码，并不能表示－3.4×10³⁸～3.4×10³⁸之间的所有数。
由此可见，规约数与非规约数的区别在于他们与0的接近程度，使用非规约浮点数的作用是避免下溢而损失过大的精度，在未使用非规约浮点数时，凡是比规约数更小的数都被直接处理为0，这样处理时损失的精度比较大，因此IEEE 754允许使用比最小规约数还要小的非规约数来表示更接近于0的数。比如float型二进制交换格式编码，规约数所能表示的最小正数是1.0×2⁻¹²⁶；非规约数所能表示的最小正数是2⁻²³×2⁻¹²⁶ =2⁻¹⁴⁹ 可以看到，规约数与非规约数的差距是2²³ 倍
现在很多计算机都支持IEEE 754标准，C++也不例外，因此我们使用编译器不能输出比非规约数还要小的数，比如对于float型二进制交换格式编码，不能输出比1.4×10⁻⁴⁵还要小的数。也就是说比1.4×10⁻⁴⁵还要小的数要么是0，要么就是1.4×10⁻⁴⁵本身。通常，比1.4×10⁻⁴⁵小，但差距不大的数，如1.2E^-45，会当作1.4×10⁻⁴⁵处理；比1.4×10⁻⁴⁵小，但差距较大的数，如2E-47，会当作0处理。比如float a = 1.3E-46; cout<<a<<endl;将输出0。

1.6 NaN简介

1、NaN分为signaling Nan(简称sNaN)和quiet NaN(简称qNaN)

sNaN提供不在本标准范围的未初始化变量和算术之类(arithmetic-like)的增强功能的表示法。说简单一点就是，sNaN用于表示未初始化变量和算术增强功能。
qNaN由实现者决定，用于提供一些回顾性(retrospective)诊断信息，说简单一点，qNaN就是用于提供一些诊断信息，通常是有关错误的信息。

2、有效载荷(payload)：是指的编码在NaN末尾有效数字段的部分，通常包含NaN的诊断信息。注：“末尾有效数字段”详见后文。

1.7 舍入和属性

1、可以使用属性来描述某个对象的某些特性，如，“人”具有“身高”、“体重”、“年龄”等属性，IEEE754也使用属性来描述某些特性。

2、IEEE754总共包含以下几大类属性：

舍入方向属性(简称舍入属性)，主要用于四舍五入
备用异常处理属性
preferredWidth(首选宽度)属性，主要用于表达式求值
value-changing optimization(值改变优化)属性，主要用于表达式求值
reproducibility(重现性)属性。

3、属性通常含有属性值，属性值可以是常量值，也可以是动态模式的值。

4、IEEE754定义了如下的舍入方向属性(rounding-direction attributes)

1)、roundTiesToEven：舍入到最接近的整数值，中间情况舍入为偶数
2)、roundTiesToAway：舍入到最接近的整数值，中间情况向远离0的方向舍入
3)、roundTowardPositive：向正无穷大方向的整数值舍入(可能是+∞)
4)、roundTowardNegative：向负无穷大方向的整数值舍入(可能是−∞)
5)、roundTowardZero：向0方向的整数值舍入

5、有关舍入属性的要求及规则

1)、对于roundTiesToEven和roundTiesToAway，若一个数的大小大于等于b^emax ( b − ½ b^1−p ) ，则必须舍入到∞，而不改变符号
2)、roundTowardPositive、roundTowardNegative、roundTowardZero是三个用户可选择的舍入方向属性，这三个属性被称为定向舍入属性(directed rounding attributes)
3)、实现必须提供roundTiesToEven和三个定向舍入属性。
4)、十进制格式实现必须提供roundTiesToAway作为用户可选择的舍入方向属性。对于二进制格式实现不需要roundTiesToAway。
5)、roundTiesToEven必须是二进制格式的结果的默认舍入方向属性。十进制格式结果的默认舍入方向属性是由语言定义的，但应该是roundTiesToEven。
6)、NaN不是四舍五入的。

6、舍入方向属性与0的符号

1)、规则1：当两个具有相反符号的操作数的和(或两个具有相同符号的操作数的差)恰好为(exactly)零时，所有舍入方向属性的和(或差)的符号必须为+0，除roundTowardNegative外
2)、规则2：在roundTowardNegative属性下，一个恰好为零的和(或差)的符号必须为− 0。
3)、规则3：但是，即使x为零，x + x = x−(−x)也会与x保持相同的符号。

示例：情形1：非roundTowardNegative属性，则
2 + (−2) = + 0，或，2 − 2 = +0 //规则1
但，
0 + 0 = +0，或，−0 − (−(−0) )= −0 //规则3，与x符号相同
情形2：roundTowardNegative属性，则
2 + (−2) = − 0，或，2 − 2 = −0 //规则2
但，
0 + 0 = 0，或，−0 − (−(−0) )= −0 //规则3，与x符号相同
4)、当(a × b) + c恰好为零时，fusedMultiplyAdd(a, b, c)的符号必须由上述操作数和的规则确定。当(a × b) + c的精确结果非零，但由于四舍五入，fusedMultiplyAdd的结果为零时，零结果取精确结果的符号。

1.8 为便于讲解本文引入如下规定及概念

1、本文将形如(−1)^sign× b^exponent× significand的表示法称为指数表示法

2、对数字的表示本文使用下标的形式表示该数的基数，若无特别说明均是指十进制数，如

1.111011₂ //一个二进制数
1.111011 //一个十进制数
1.111011₁₆ //一个16进制数

3、本文尽量不使用浮点数据的三元组表示法，而使用指数表示法

4、本文对于NaN与qNaN、sNaN的区别不作严格区分，也不对浮点数据表示法及其值作严格的区分。

5、本文将未编码的浮点数据称为真实浮点数据或真实数据，其相应参数被称为真实参数，如指数e称为真实指数

6、在计算机中浮点数通常分为单精度(float型)和双精度(double型)，float型通常使用32位存储，double使用64位存储，本文重点以float型(32位)为示例进行讲解。

7、本文将有效数通常称为尾数，这样做的目的，主要是更方便理解，但IEEE754-2008并不称其为尾数。

8、英文单词的重点区别

需要重点区分bit(位)与digit(位数)的区别，bit重点强制二进制数的位数(即比特位)，而digit重点强调十进制数的位数。如，有效数位(significance bit)，可理解为“尾数位(指比特位)”，为表述准确，也可译为“有效数比特位”；而有效数位数(significand digit)，重点强调的是十进制数的位数，可理解为“尾数位数(指十进制数的位数)”，本文在易引起混淆的地方，会注明英文单词。