本文主要是介绍计算机基础——IEEE754标准的浮点数的转化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
IEEE754是现在公认的、最广泛使用的浮点数转换运算标准,为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式(包括负零-0)与反常值(denormal number)),一些特殊数值(无穷(Inf)与非数值(NaN)),以及这些数值的“浮点数运算符”;它也指明了四种数值舍入规则和五种例外状况(包括例外发生的时机与处理方式)。
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)。只有32位模式有强制要求,其他都是选择性的。大部分编程语言都有提供IEEE浮点数格式与算术,但有些将其列为非必需的。例如,IEEE 754问世之前就有的C语言,现在有包括IEEE算术,但不算作强制要求(C语言的float通常是指IEEE单精确度,而double是指双精确度)。
下面主要讲述单精度(float),双精度(double)和单精度一样,使用例子来说明转化过程。
(1)float a = -12.75; a的机器码是多少?(采用IEEE754标准)
- 不规范的表示:-12.75
- 转换整数部分:
12 = 8 + 4 = 1100(二进制) - 转换小数部分:
.75 = .5 + .25 = .11(二进制) - 把两部分组装起来,变成标准化:
1100.11 = 1.10011*2^3 - 转换指数部分:
127 + 3 = 128 + 2 = 1000 0010(二进制) - 故结果为:
1 1000 0010100 1100 0000 0000 0000 0000(二进制) - 十六进制表示:
0XC14C0000(十六进制)
(2)二进制1011 11101 110 0000 0000 0000 0000 0000转化为float是多少?(采用IEEE754标准)
![]()
- Sign:1 => negative(符号位)
- Exponent:
0111 1101(二进制) = 125(10进制)
减去偏置常数:125 - 127 = -2 - Significand:
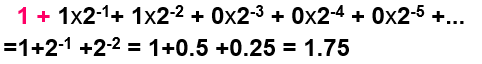
- Repersents:-1.75(十进制)*2^(-2) = -0.4375
(3)double num = 10.5的二进制是多少?
- 10.5 = 1010.1 = 1.0101 * 2^3
- 符号位 S=1,阶码 exp = 3 + 1023 = 100 0000 0010B(double 阶码为 11 位),
- 尾数: 0101 [0000](double 尾数为 52 位)
- 则其机器数为: 0 100 0000 0010 0101 [0000]= 0x4025 0000 0000 0000
这篇关于计算机基础——IEEE754标准的浮点数的转化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





