day38专题
Java高级Day38-网络编程作业
112.网络编程作业 //1.使用字符流的方式,编写一个客户端程序和服务器端程序//2.客户端发送"name",服务器端接收到后,返回"我是nova"//3.客户端发送"hobby",服务器端接收到后,返回"编写java程序"//4.不是这两个问题,回复"你说啥呢"===============//客户端//===============public class SocketT
代码随想录冲冲冲 Day38 动态规划Part6
322. 零钱兑换 最大最小值的问题 这样的问题不需要考虑遍历顺序 但是这道题需要注意的是红线的两个部分 这两个部分的意思是一样的 首先dp[j]代表的是amount为j的时候 最小的硬币数量 如果说任何的dp[j]为INT_MAX也就是初始值,这就说明这哥mount的数量没有得到或者得不到 那么就不能继续更新了加入j =5 有可能 j=4根本得不到 那么由dp[4] +1就不合理了
代码随想录训练营 Day38打卡 动态规划 part06 322. 零钱兑换 279. 完全平方数 139. 单词拆分
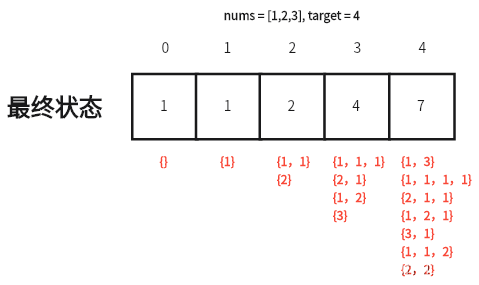
代码随想录训练营 Day38打卡 动态规划 part06 一、力扣322. 零钱兑换 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示例: 输入:coins = [1, 2, 5], amount = 1
【代码随想录训练营第42期 Day38打卡 - 动态规划Part6 - LeetCode 322. 零钱兑换 279.完全平方数 139.单词拆分
目录 一、做题心得 二、题目与题解 题目一:322. 零钱兑换 题目链接 题解:动态规划--完全背包 题目二: 279.完全平方数 题目链接 题解:动态规划--完全背包 题目三:139.单词拆分 题目链接 题解:动态规划--完全背包 三、小结 一、做题心得 今天来到了代码随想录动态规划章节的Part6,依旧是完全背包问题的应用。相对于前边直接套用模板,今天
代码随想录 day37|day38|day39
贪心续 合并区间 题意:将重合的区间合并。 思路:先把区间按照左端点排序。之后使用一个st表示左端点,ed表示右端点,如果区间是分离的那么就把先的区间加入到集合。 代码 struct comp{bool operator()(const vector<int> &lhs ,const vector<int> &rhs){if(lhs[0]<rhs[0]){return true ; }ret
【代码随想录算法训练Day38】LeetCode 509.斐波纳契数、LeetCode 76.爬楼梯、LeetCode 746. 使用最小花费爬楼梯
Day38 动态规划 又开始了新的章节,有了点难度的感觉。。 动态规划五部曲: 确定dp数组(dp table)以及下标的含义 确定递推公式 dp数组如何初始化 确定遍历顺序 举例推导dp数组 这些以后慢慢参透 LeetCode 509.斐波纳契数 最简单的动态规划,甚至不需要动态规划就可以解决的问题。初始状态、递推公式都已经有了,这道题就很简单了。 class Solution {pu
代码随想录算法训练营Day38|动态规划理论基础、2.斐波那契数、3.爬楼梯、4.使用最小花费爬楼梯
动态规划理论基础 代码随想录 (programmercarl.com) 动态规划(Dynamic Programming,简称DP)是一种算法设计技术,它通过将复杂问题分解为更小的子问题来解决优化问题。动态规划通常用于解决那些具有重叠子问题和最优子结构特性的问题。(可以理解为一种递推) 重叠子问题: 在递归算法中,相同的子问题会被多次计算。动态规划通过存储这些子问题的解来避
day38 ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1F(n) = F(n - 1) + F(n - 2),其中 n > 1 给定 n ,请计算 F(n) 。 示例 1: 输入:n = 2输出:1解释:F(2) = F(1) +
【前端每日基础】day38——v-for 的 diff 算法的原理
Vue.js 的 v-for 指令用于渲染列表,内部通过一个高效的 diff 算法来确保 DOM 更新的性能。下面详细介绍 v-for 的 diff 算法原理。 Diff 算法概述 Diff 算法的目标是在新旧虚拟 DOM 树之间找到最小的变更,并将这些变更应用到实际的 DOM 上。这个过程包括以下步骤: 同层比较:只比较同一层次的节点,不跨层次比较。 节点比较:通过比较节点的 key 值来判
《python编程从入门到实践》day38
# 昨日知识点回顾 定义、迁移模型Entry # 今日知识点学习 18.2.7 Django shell 每次修改模型后,看到重启后的效果需要重启shell,退出shell会话Windows系统按ctrl+Z或者输入exit() 18.3 创建页面:学习笔记主页 创建页面三阶段:定义URL
代码随想录算法训练营第36期DAY38
DAY38 435无重叠区间 昨晚很快就想出来了,今天相当于二刷。 class Solution {public: static bool mycmp(vector<int>&a,vector<int>&b){ return a[1]<b[1]; } int eraseOverlapIntervals(vector<vector<int>>& interval
代码随想录训练营Day38、39:Leetcode509、70、746、62、63
Leetcode509: 问题描述: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1F(n) = F(n - 1) + F(n - 2),其中 n > 1 给定 n ,请计算 F(n) 。 示例 1: 输入:n = 2输出:1解释:F(2) =
代码随想录35期Day38-Java(Day37休息)
Day38题目 LeetCode509.斐波那契数列 核心思想:很简单dp[i]=dp[i-1]+dp[i-2].这里用了数组存储的形式,也可以递归 class Solution {public int fib(int n) {int[] dp = new int[n+2];dp[0] = 0;dp[1] = 1;for(int i = 2 ; i <= n ; i ++){dp[i] =
代码随想录算法训练营Day38 | 动态规划理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯 | Python | 个人记录向
注:Day37休息。 本文目录 动态规划理论基础509. 斐波那契数做题看文章 70. 爬楼梯做题看文章空间复杂度为O(n)版本空间复杂度为O(3)版本 746. 使用最小花费爬楼梯做题看文章 以往忽略的知识点小结个人体会 动态规划理论基础 代码随想录:动态规划理论基础 动规五部曲: 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举
代码随想录算法训练营Day38 | 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
代码随想录算法训练营Day38 | 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯 LeetCode 509. 斐波那契数 题目链接:LeetCode 509. 斐波那契数 思路: 维护两个数组即可。确定dp0和dp1以及状态转移条件。 class Solution {public:int fib(int n) {if(n<=1) return n; int dp[2
Day38 斐波那契数 + 爬楼梯 + 使用最小花费爬楼梯
509 斐波那契数 题目链接:509. 斐波那契数 - 力扣(LeetCode) 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给定 n ,请计算 F(n) 。 输入:n = 2输出
【每日刷题】Day38
【每日刷题】Day38 🥕个人主页:开敲🍉 🔥所属专栏:每日刷题🍍 🌼文章目录🌼 1. 2696. 删除子串后的字符串最小长度 - 力扣(LeetCode) 2. LCR 123. 图书整理 I - 力扣(LeetCode) 3. 面试题 02.06. 回文链表 - 力扣(LeetCode) 1. 2696. 删除子串后的字符串最小长度 - 力扣(Leet
代码随想录算法训练营DAY38|C++动态规划Part.1|动态规划理论基础、509.斐波那契数、70.爬楼梯、746.使用最小花费爬楼梯
文章目录 动态规划理论基础什么是动态规划动态规划的解题步骤DP数组以及下标的含义递推公式DP数组初始化DP数组遍历顺序打印DP数组动态规划五部曲 动态规划应该如何debug 509.斐波那契数什么是斐波那契数列动态规划五部曲确定dp数组下标以及含义确定递推公式dp数组如何初始化确定遍历顺序打印DP数组 代码实现CPP代码 70.爬楼梯题意分析动规五部曲确定dp数组下标以及含义确定递推公式dp
【力扣一刷】代码随想录day38(动态规划part1:509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼)
目录 【动态规划理论基础】 【509. 斐波那契数】简单题 方法一 用额外的数组存储每个状态 方法二 用2个遍历存储前两个状态(减小空间复杂度) 【70. 爬楼梯】简单题 【746. 使用最小花费爬楼】简单题 【动态规划理论基础】 1、定义:英文为Dynamic Programming,简称DP 2、步骤: 确定变量 f(i) 的含义确定递推公式:如 f(i) 和 f
代码随想录算法训练营day38
509. 斐波那契数 五部曲: dp数组下标及含义:dp[i]表示第i个斐波那契数的值dp数组初始化:dp[0]=0,dp[1]=1递推公式:dp[i] = dp[i - 1] + dp[i - 2]遍历方向:从前往后dp数组推到举例:0,1,1,2,3,5,8,13 class Solution {public:int fib(int n) {if(n<1) return n;vecto
Day38 代码随想录(1刷)动态规划
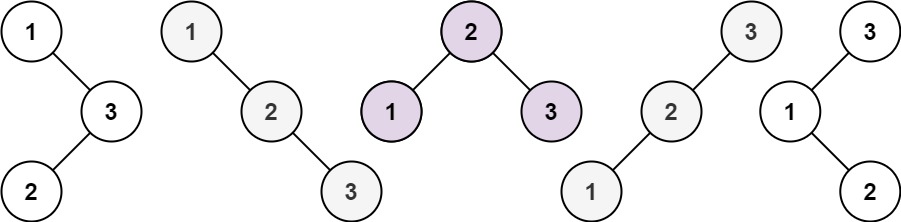
目录 343. 整数拆分 96. 不同的二叉搜索树 343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n = 2输出: 1解释: 2 = 1 + 1, 1 × 1 = 1。 示例 2: 输入: n = 10输出: 36解释: 10 = 3 + 3
备战蓝桥杯Day38 - 第11届python组真题 - A门牌制作
A 门牌制作 1、题目描述 2、使用到的包 collections collections 模块提供了一些有用的容器数据类型,这些类型提供了比Python内置的列表、元组、字典和集合更特定的功能。在这道题目中使用到了collections 中的counter模块 counter主要是用来统计可遍历类型(列表、元组)中元素的个数。 功能就跟用字典实现哈希表一样,相当于对哈希表进行了封
【JavaWeb】Day38.MySQL概述——数据库设计-DQL
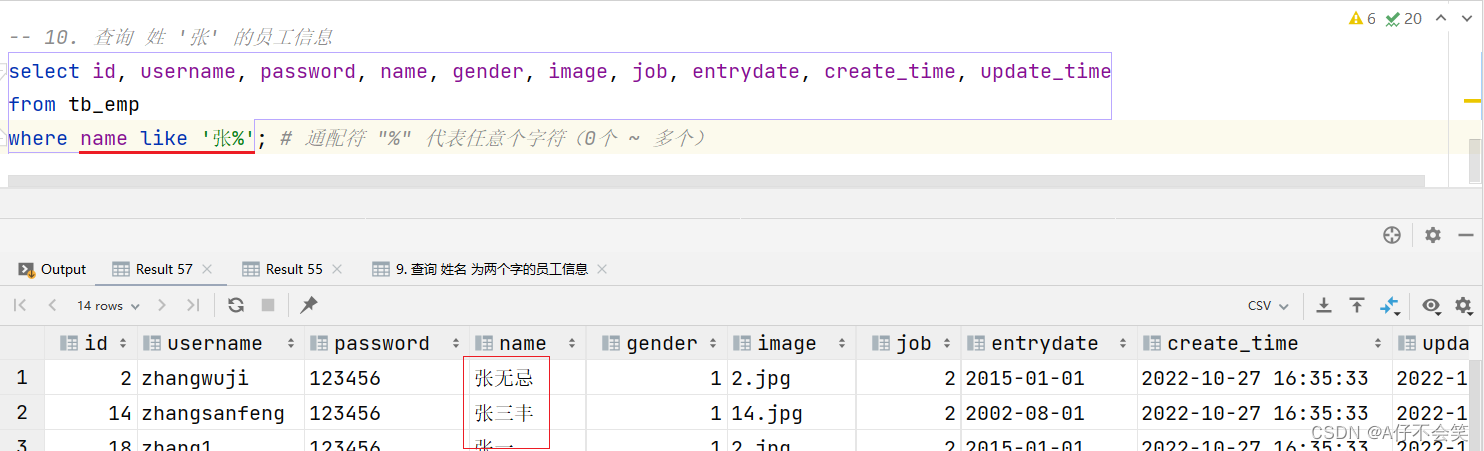
数据库设计——DQL 介绍 DQL英文全称是Data Query Language(数据查询语言),用来查询数据库表中的记录。 查询关键字:SELECT 查询操作是所有SQL语句当中最为常见,也是最为重要的操作。在一个正常的业务系统中,查询操作的使用频次是要远高于增删改操作的。当我们打开某个网站或APP所看到的展示信息,都是通过从数据库中查询得到的,而在这个查询过程中,
代码随想录 day38 第九章 动态规划part01
● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯 理论基础 解决动态规划必须要想清楚的点 dp数组以及下标的含义递推公式dp数组如何初始化遍历顺序打印数组 检查结果 1. 斐波那契数 关联 leetcode 509. 斐波那契数 思路 动规五部曲 dp数组以及下标的含义 dp[i] 就是第 i 个斐波那契数的值 递推