仿射变换（AffineTransform）与仿射矩阵

本文主要是介绍仿射变换（AffineTransform）与仿射矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

仿射变换（Affine transformation），又称仿射映射，是指在几何中，对一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

它是一种二维坐标到二维坐标间的线性变换，保持了二维图形的“平直性”（直线经过变换之后依然是直线）和“平行性”（二维图形之间的相对位置关系保持不变，平行线依然是平行线，且直线上点的位置顺序不变）。
在这里插入图片描述

任意的仿射变换都能表示成“乘以一个矩阵(线性变换)，再加上一个向量 (平移) 的形式”。

仿射变换

仿射变换包含geometric contraction、expansion、dilation、reflection、rotation、shear、similarity transformations、spiral similarities和translation等类别及它们的组合，通常来讲，可以简单地认为仿射变换由rotations、translations、dilations和shears四类组合而成。

在这里插入图片描述

实际上“仿射变换”可以看成基础的“线性变换”+“平移”的组合。而“线性变换”要求变换前是直线的变换后仍然是直线，且直线之间的比例保持不变，同时原点本质保持不变。
在这里插入图片描述
OpenCV封装了仿射变换的函数可供调用：

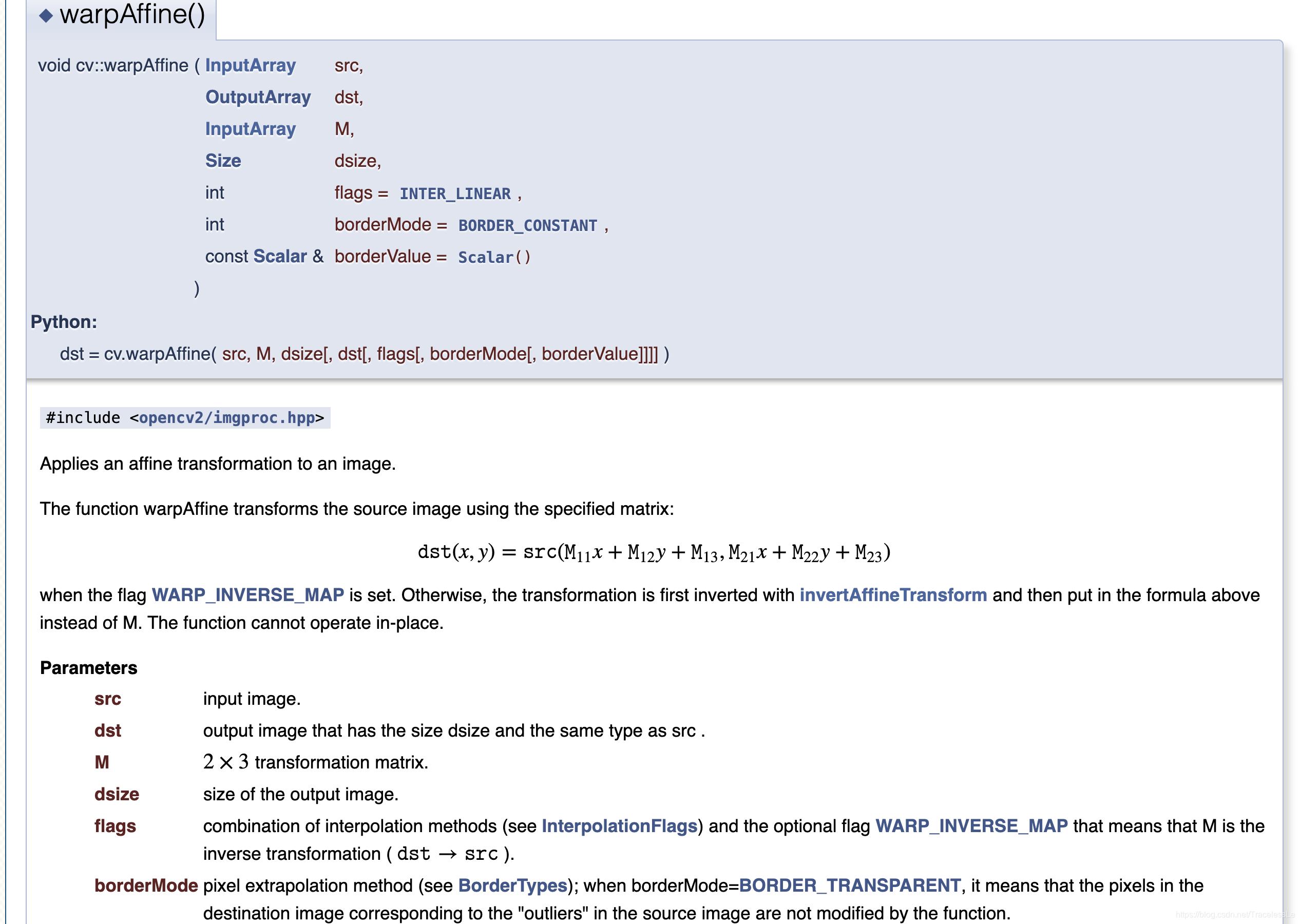
仿射矩阵

在这里插入图片描述
对于二维图像而言，仿射变换可以表示成矩阵相乘形式。

（1）平移量为0的仿射变换称为线性变换，可以用下列矩阵表示：
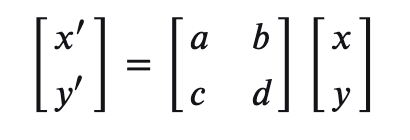
在这里插入图片描述
（2）只有平移变换而没有线性变换的仿射变换，可以用下列矩阵表示：

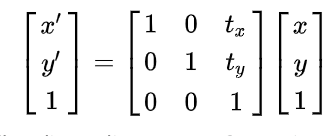
将同时含有线性变换和平移变换的仿射变换，用下列矩阵表示：

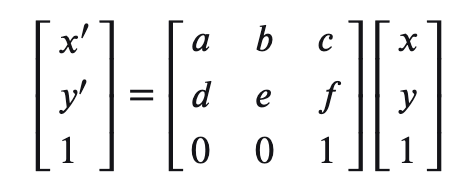
则变换矩阵为：

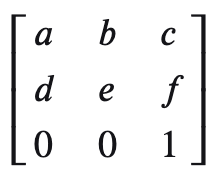
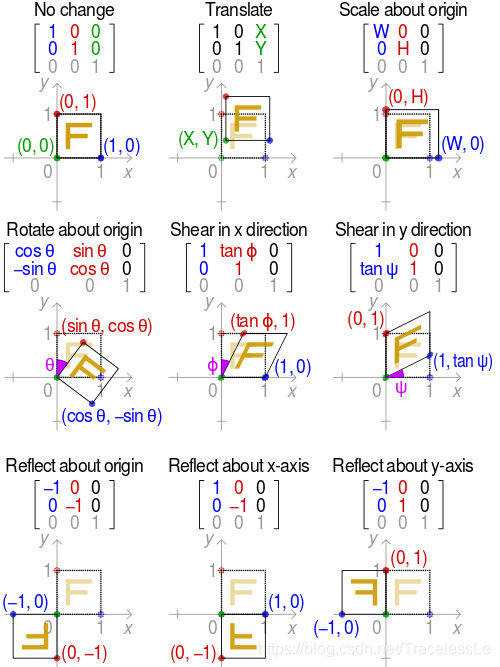
不同的仿射变换类型，其仿射矩阵参数a~f不同。维基百科中有一个非常直观地描述放射矩阵对应仿射变换效果的图示，如下所示：
在这里插入图片描述
对应二维图像而言，仿射矩阵的求解，需要至少三个非共线的点的映射关系。其中一个对应点可以列一个线性方程，三个对应点可以列出线性方程组，可以采用最小二乘法或者SVD分解法等方法进行求解。

常用的求解仿射矩阵的函数有OpenCV的getAffineTransform() 方法和
scikit-image (skimage) 的transform.SimilarityTransform.estimate()方法。
在这里插入图片描述

其中skimage的transform.SimilarityTransform.estimate()方法则是采用最小均方估计的umeyama算法实现。

在这里插入图片描述

逆仿射变换与其矩阵

对于仿射变换，我们在某些应用场景下需要进行其逆变换，即将变换后的图片再变换回原来的位置。

此时，我们需要对所求的仿射矩阵求逆矩阵，通过逆矩阵做仿射变换则可以回到原先的图片位置状态。

求二阶矩阵的逆矩阵，有：
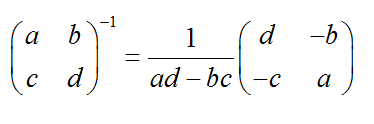
在这里插入图片描述
其中 $a d - b c \neq = 0$

OpenCV中实现的仿射矩阵的逆矩阵求解也用了这一推论：
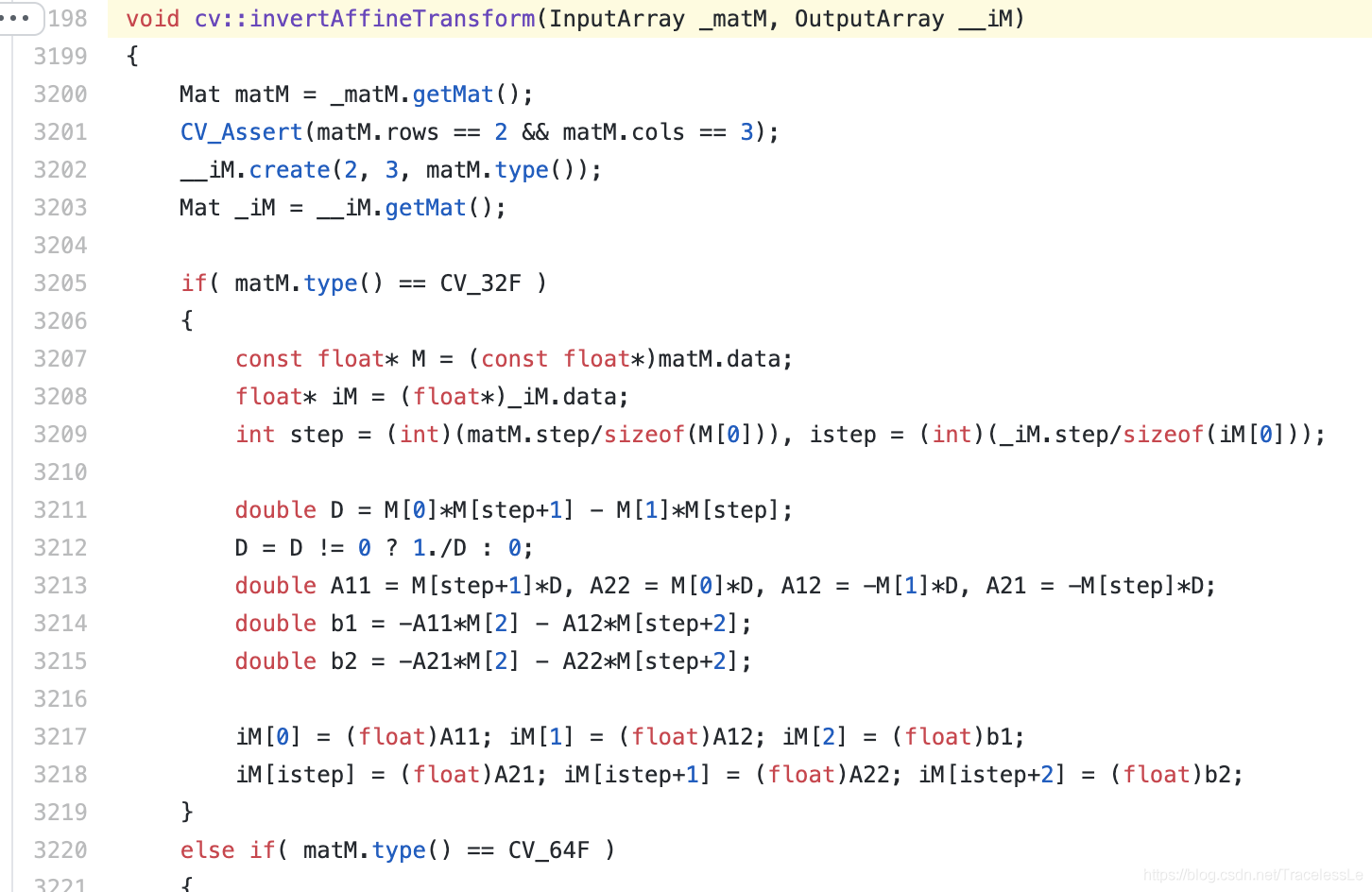
在这里插入图片描述
利用求出的逆矩阵，再进行仿射变换，即可得到原仿射变换前的状态。

在这里插入图片描述

参考资料

[1] 仿射变换 - 维基百科，自由的百科全书
[2] Affine transformation - Wikipedia
[3] Affine Transformation – from Wolfram MathWorld
[4] 仿射变换及其变换矩阵的理解 - shine-lee - 博客园
[5] 如何通俗地讲解「仿射变换」这个概念？ - 知乎
[6] OpenCV: Geometric Image Transformations
[7] 图像处理的仿射变换与透视变换
[8] OpenCV：图像变换-仿射变换与透视变换研究_SSS_369-CSDN博客
[9] OpenCV-Python教程:12.图片的几何转换 - 简书
[10] opencv_attic/imgwarp.cpp · opencv/opencv_attic
[11] 人脸对齐中的相似性变换_yiran103的专栏-CSDN博客
[12] 图像的几何变换 — OpenCV-Python Tutorials 文档
[13] Module: transform — skimage v0.18.0.dev0 docs
[14] Module: transform.SimilarityTransform — skimage v0.18.0.dev0 docs
[15] scikit-image/_geometric.py · scikit-image/scikit-image
[16] skimage库的transform.SimilarityTransform()用法_小C的博客-CSDN博客
[17] OpenCV: Image Warping
[18] opencv_contrib/warp.cpp · opencv/opencv_contrib
[19] opencv_contrib/warp.cu · opencv/opencv_contrib
[20] Transformation matrix - Wikipedia