15_岭回归-Ridge、岭回归API、线性回归和岭回归的对别；逻辑回归、sigmoid函数、逻辑回归公式、损失函数、逻辑回归API、逻辑回归案例、逻辑回归的优缺点、逻辑回归 VS 线性回归等

2024-04-19 17:32
文章标签 公式 函数 15 逻辑 vs api 案例 回归 线性 优缺点 损失 sigmoid ridge 对别

本文主要是介绍15_岭回归-Ridge、岭回归API、线性回归和岭回归的对别；逻辑回归、sigmoid函数、逻辑回归公式、损失函数、逻辑回归API、逻辑回归案例、逻辑回归的优缺点、逻辑回归 VS 线性回归等，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、岭回归

岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

1.1 Ridge线性回归sklearn API

sklearn.linear_model.Ridge

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)
带有L2正则化的线性最小二乘法。该模型求解回归模型，其中损失函数是线性最小二乘函数，并且正则化由l2范数给出。 也称为Ridge回归或Tikhonov正则化。 该估计器具有对多变量回归的内置支持（即，当y是形状的2d阵列[n_samples，n_targets]时）。参数：
alpha：{float，array-like}，shape（n_targets）正则化强度; 必须是正浮点数。 正则化改善了问题的条件并减少了估计的方差。 较大的值指定较强的正则化。 Alpha对应于其他线性模型（如Logistic回归或LinearSVC）中的C^-1。 如果传递数组，则假定惩罚被特定于目标。 因此，它们必须在数量上对应。  
copy_X：boolean，可选，默认为True如果为True，将复制X; 否则，它可能被覆盖。 
fit_intercept：boolean是否计算此模型的截距。 如果设置为false，则不会在计算中使用截距（例如，数据预期已经居中）。
max_iter：int，可选共轭梯度求解器的最大迭代次数。 对于'sparse_cg'和'lsqr'求解器，默认值由scipy.sparse.linalg确定。 对于'sag'求解器，默认值为1000。  
normalize：boolean，可选，默认为False如果为真，则回归X将在回归之前被归一化。 当fit_intercept设置为False时，将忽略此参数。 当回归量归一化时，注意到这使得超参数学习更加鲁棒，并且几乎不依赖于样本的数量。 相同的属性对标准化数据无效。 然而，如果你想标准化，请在调用normalize = False训练估计器之前，使用preprocessing.StandardScaler处理数据。
solver：{'auto'，'svd'，'cholesky'，'lsqr'，'sparse_cg'，'sag'}用于计算的求解方法：'auto'根据数据类型自动选择求解器。'svd'使用X的奇异值分解来计算Ridge系数。对于奇异矩阵比'cholesky'更稳定。'cholesky'使用标准的scipy.linalg.solve函数来获得闭合形式的解。'sparse_cg'使用在scipy.sparse.linalg.cg中找到的共轭梯度求解器。作为迭代算法，这个求解器比大规模数据（设置tol和max_iter的可能性）的“cholesky”更合适。'lsqr'使用专用的正则化最小二乘常数scipy.sparse.linalg.lsqr。它是最快的，但可能不是在旧的scipy版本可用。它还使用迭代过程。'sag'使用随机平均梯度下降。它也使用迭代过程，并且当n_samples和n_feature都很大时，通常比其他求解器更快。注意，“sag”快速收敛仅在具有近似相同尺度的特征上被保证。您可以使用sklearn.preprocessing的缩放器预处理数据。所有最后四个求解器支持密集和稀疏数据。但是，当fit_intercept为True时，只有'sag'支持稀疏输入。
新版本0.17支持：随机平均梯度下降解算器。
tol:float解的精度
random_state : int seed,RandomState实例或None(默认)伪随机数生成器的种子，当混洗数据时使用。仅用于'sag'求解器。最新版本0.17：random_sate支持随机平均渐变。属性：
coef_：array，shape（n_features，）或（n_targets，n_features）权重向量。
intercept_：float | array，shape =（n_targets,）决策函数的独立项，即截距。如果fit_intercept
n_iter_：array或None，shape（n_targets,）每个目标的实际迭代次数。 仅适用于sag和lsqr求解器。其他求解器将返回None。在版本0.17中出现。方法：
fit(self, X, y[, sample_weight])   : Fit Ridge回归模型
get_params(self[, deep])           : 获取此估计器的参数。
predict(self, X)                   : 使用线性模型进行预测
score(self, X, y[, sample_weight]) : 返回预测的确定系数R ^ 2
set_params(self, \*\*params)       : 设置estimator的参数

案例：

# -*- coding: utf-8 -*-from sklearn.linear_model import Ridge
import numpy as npn_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
print(y)print("---------------------------------")X = rng.randn(n_samples, n_features)
print(X)print("---------------------------------")
clf = Ridge(alpha=1.0)
clf.fit(X, y)
print(clf.coef_)

输出结果：

[ 1.76405235  0.40015721  0.97873798  2.2408932   1.86755799 -0.977277880.95008842 -0.15135721 -0.10321885  0.4105985 ]
---------------------------------
[[ 0.14404357  1.45427351  0.76103773  0.12167502  0.44386323][ 0.33367433  1.49407907 -0.20515826  0.3130677  -0.85409574][-2.55298982  0.6536186   0.8644362  -0.74216502  2.26975462][-1.45436567  0.04575852 -0.18718385  1.53277921  1.46935877][ 0.15494743  0.37816252 -0.88778575 -1.98079647 -0.34791215][ 0.15634897  1.23029068  1.20237985 -0.38732682 -0.30230275][-1.04855297 -1.42001794 -1.70627019  1.9507754  -0.50965218][-0.4380743  -1.25279536  0.77749036 -1.61389785 -0.21274028][-0.89546656  0.3869025  -0.51080514 -1.18063218 -0.02818223][ 0.42833187  0.06651722  0.3024719  -0.63432209 -0.36274117]]
---------------------------------
[ 0.51088991  0.03729032 -0.65075201  0.0930311   0.93380887]

1.2 线性回归 LinearRegression与Ridge对比

岭回归： 回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。

2 分类算法–逻辑回归

逻辑回归，用于表达某件事情发生的可能性
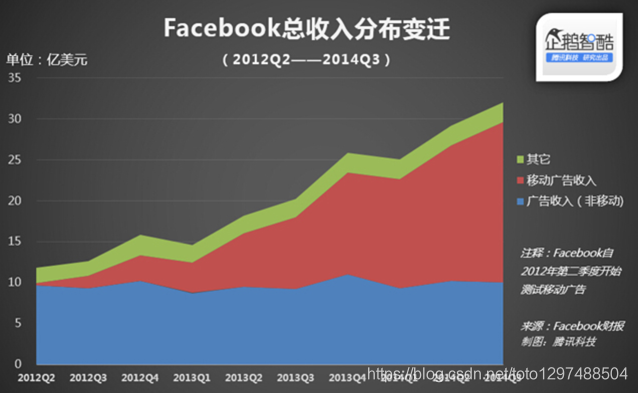
在这里插入图片描述
通过上面的图获得：

  1. 广告点击率
  2. 判断用户的性别
  3. 预测用户是否会购买给定的商品类
  4. 判断一条评论是正面的还是负面的

还比如还可以做以下事情：
1、一封邮件是垃圾邮件的可能性（是，不是）
2、你购买一件商品的可能性（买、不买）
3、广告被点击的可能性（点、不点）

通过上图的数据，获得上面4个方面的信息，就可以使用逻辑回归。

逻辑回归是解决二分类问题的利器
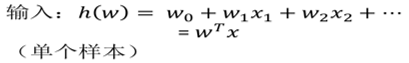
在这里插入图片描述

2.1 sigmoid函数

在这里插入图片描述

2.2 逻辑回归公式

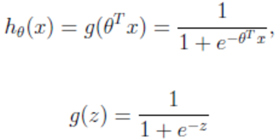
在这里插入图片描述
输出：[0,1]区间的概率值，默认0.5作为阀值
注：g(z)为sigmoid函数

2.3 逻辑回归的损失函数、优化(了解)

与线性回归原理相同,但由于是分类问题，损失函数不一样，只能通过梯度下降求解

对数似然损失函数：
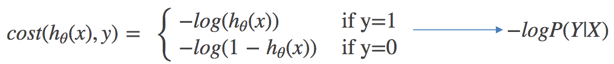
在这里插入图片描述
完整的损失函数：
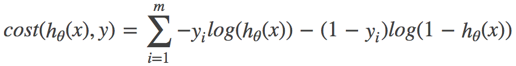
在这里插入图片描述
cost损失的值越小，那么预测的类别准确度更高。
当y=1时：
在这里插入图片描述
在这里插入图片描述

2.4 二分类问题

二分类问题是指预测的y值只有两个取值（0或1），二分类问题可以扩展到多分类问题。例如：我们要做一个垃圾邮件过滤系统，x是邮件的特征，预测的y值就是邮件的类别，是垃圾邮件还是正常邮件。对于类别我们通常称为正类（positive class）和负类（negative class），垃圾邮件的例子中，正类就是正常邮件，负类就是垃圾邮件。

2.5 sklearn逻辑回归API

sklearn.linear_model.LogisticRegression 可以用于概率预测、分类等。
逻辑回归用于离散变量的分类，即它的输出y的取值范围是一个离散的集合，主要用于类的判别，而且其输出值y表示属于某一类的率。

Logistic Regression 逻辑回归主要用于分类问题，常用来预测概率，如知道一个人的年龄、体重、身高、血压等信息，预测其患心脏病的概率是多少。经典的LR用于二分类问题（只有0,1两类）。

class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’liblinear’, max_iter=100, multi_class=’ovr’, verbose=0, warm_start=False, n_jobs=1)

注意：
（1）在多类别划分中，如果’multi_class’选项设置为’ovr’，训练算法将使用one-vs-rest(OvR)方案；如果’multi_class’选项设置为‘多项式’，则使用交叉熵损失。
（2）这个类使用’liblinear’ 、‘library’、‘newton-cg’、‘sag’ 和 ‘lbfgs’ 求解器实现了规范化的logistic回归。它的输入矩阵可以是密集和稀疏的矩阵；使用C-ordered arrays or CSR matrices containing 64-bit floats可以获得最佳的性能。
（3）‘newton-cg’、‘sag’、and 'lbfgs’求解器只支持原始公式下的L2正则化；liblinear求解器同时支持L1和L2的正则化，只对L2处罚采用对偶公式。

参数说明：
penalty :str，‘l1’ or ‘l2’,default : ‘l2’。用来指定惩罚的标准，‘newton-cg’、‘sag’ 和 ‘lbfg’ solvers仅支持l2 惩罚。

  1. 如果为’l2’，则优化目标函数为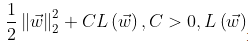：在这里插入图片描述为极大似然函数。
  2. 如果为’l1’，则优化目标函数为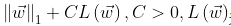：在这里插入图片描述为极大似然函数。
  3. ‘l1’ : 正则化的损失函数不是连续可导的，而’netton-cg’,‘sag’,'lbfgs’三种算法需要损失函数的一阶或二阶连续可导。
  4. 调参时如果主要是为了解过拟合，选择’l2’正则化就够了。若选择’l2’正则化还是过拟合，可考虑’l1’正则化。
  5. 若模型特征非常多，希望一些不重要的特征系数归零，从而让模型系数化的话，可使用’l1’正则化。

dual :一个布尔值，默认是False。选择目标函数为原始形式还是对偶形式。如果为True，则求解对偶形式（只是在penalty=‘l2’ 且solver='liblinear’有对偶形式）；如果为False，则求解原始形式。（bool, default: False。Dual or primal formulation.Dual formulation只适用于 l2 penalty with liblinear solver.Prefer dual=False when n_samples > n_features）
注意： ：将原始函数等价转化为一个新函数，该新函数称为对偶函数。对偶函数比原始函数更易于优化。

tol : float, default: 1-4。Tolerance for stopping criteria。（指定判断迭代收敛与否的一个阈值）（优化算法停止的条件。当迭代前后的函数差值小于等于tol时就停止）
C : 一个浮点数，默认：1.0，它指定了惩罚系数的倒数。如果它的值越小，则正则化越大。（逆正则化的强度，一定要是整数，就像支持向量机一样，较小的值有职责更好的正则化）
fit_intercept : 一个布尔值，默认为True，指定是否存在截距，默认存在。如果为False，则不会计算b值（模型会假设你的数据已经中心化）。（选择逻辑回归模型中是否会有常数项）
intercept_scaling : 一个浮点数，只有当solver=‘liblinear’才有意义。当采用fit_intercept时，相当于人造一个特征出来，该特征恒为1，其权重为b。在计算正则化项的时候，该人造特征也被考虑了。因此为了降低人造特征的影响，需要提供 intercept_scaling。
class_weight : 一个字典或者字符串’balanced’。用于表示分类中各种类型的权重，可以不输入，即不考虑权重。如果输入的话可以调用balanced库计算权重，或者是手动输入各类的权重。比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1},这样类型0的权重为90%，而类型1的权重为10%。

  1. 如果为字典：则字典出了每个分类的权重，如{class_label:weight}
  2. 如果为字符串 ‘balanced’：则每个分类的权重与该分类在样品中出现的频率成反比。
  3. 如果未指定，则每个分类的权重都为1。

max_iter : 一个整数，默认：100，指定最大迭代数。仅仅针对solvers为newton-cg,sag和lbfgs

random_state : 一个整数或者一个RandomState实例，或者None。（随机数种子，默认为无，仅在正则化优化算法为sag,liblinear时有用）

  1. 如果为整数，则它指定了随机数生成器的种子。

  2. 如果为RandomState实例，则指定了随机数生成器。

  3. 如果为None，则使用默认的随机数生成器。
    solver : 一个字符串，指定了求解最优化问题的算法，可以为如下的值。

  4. ‘newton-cg’：使用牛顿法。

  5. ‘lbfgs’：使用L-BFGS拟牛顿法。（拟牛顿法的一种。利用损失函数二阶倒数矩阵即海森矩阵来迭代损失函数）

  6. ‘liblinear’ ：使用 liblinear。（使用坐标轴下降法来迭代化损失函数）

  7. ‘sag’：使用 Stochastic Average Gradient descent 算法。（随机平均梯度下降。每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候）

  8. ‘saga’
    注意：

  9. 对于规模小的数据集，'liblearner’比较适用；对于规模大的数据集，'sag’比较适用。

  10. 对于多级分类的问题，只有’newton-cg’,‘sag’,‘saga’和’lbfgs’,libniear只支持多元逻辑回归的OvR，不支持MvM，但MVM相对精确。(对于MvM，若模型有T类，每次在所有的T类样本里面选择两类样本出来，把所有输出为该两类的样本放在一起，进行二元回归，得到模型参数，一共需要T(T-1)/2次分类。）

  11. ‘newton-cg’、‘lbfgs’、‘sag’ 只处理penalty=‘12’的情况。相反的’liblinear’和’saga’处理L1惩罚。
    multi_class : 一个字符串，指定对于多分类问题的策略，可以为如下的值。

  12. ‘ovr’ ：采用 one-vs-rest 策略。

  13. ‘multinomial’：直接采用多分类逻辑回归策略。
    verbose : 一个正数。用于开启/关闭迭代中间输出的日志。（日志冗长度int：冗长度；0：不输出训练过程；1：偶尔输出； >1：对每个子模型都输出）
    warm_start : 一个布尔值，默认False。是否热启动，如果为True，那么使用前一次训练结果继续训练，否则从头开始训练。
    n_jobs : 并行数，int : 个数。-1，跟CPU核数一致；1 ： 默认值。

返回值：
coef_ : 权重向量。shape (1, n_features) or (n_classes, n_features)
intercept : 截距。shape (1,) or (n_classes,)
n_iter_ : 所有类的实际迭代次数。shape (n_classes,) or (1, )

方法
fix(X,y[,sample_weight])：根据给出的训练数据来训练模型。用来训练LR分类器，其中X是训练样本，y是对应的标记样本。
predict(X)：用模型进行预测，返回预测值。(用来预测测试样本的标记，也就是分类。预测x的标签)
score(X,y[,sample_weight])：返回（X，y）上的预测准确率（accuracy）。
predict_log_proba(X)：返回一个数组，数组的元素依次是 X 预测为各个类别的概率的对数值。
predict_proba(X)：返回一个数组，数组元素依次是 X 预测为各个类别的概率的概率值。
sparsify() : 将系数矩阵转换为稀疏格式。
set_params(params) : 设置此估计器的参数。
get_params([deep]) ： Get parameters for this estimator;
decision_function(X) : 预测样本的置信度分数。
densify() : 将系数矩阵转换为密集阵列格式。

sklearn.linear_model.LogisticRegressionCV
相比于LogisticRegression,LogisticRegressionCV使用交叉验证来选择正则化系数C。

2.6 LogisticRegression回归案例

良／恶性乳腺癌肿瘤预测
原始数据的下载地址：https://archive.ics.uci.edu/ml/machine-learning-databases/
具体的是：https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data
内容如下：
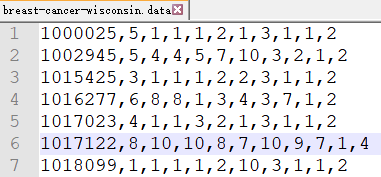
在这里插入图片描述

数据描述：
（1）699条样本，共11列数据，第一列用语检索的id，后9列分别是与肿瘤相关的医学特征，最后一列表示肿瘤类型的数值。
（2）包含16个缺失值，用”?”标出。

2.6.1 良／恶性乳腺癌肿瘤分类流程

  1. 网上获取数据（工具pandas）
  2. 数据缺失值处理、标准化
  3. LogisticRegression估计器流程

案例：

# -*- coding: utf-8 -*-from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
import pandas as pd
import numpy as npdef logistic():"""逻辑回归做二分类进行癌症预测（根据细胞的属性特征）:return:"""# 构造列标签名字column = ['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']# 读取数据data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data", names=column)print(data)# 缺失值进行处理data = data.replace(to_replace='?', value=np.nan)data = data.dropna()# 进行数据的分割x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]], data[column[10]], test_size=0.25)# 产品标准化处理std = StandardScaler()x_train = std.fit_transform(x_train)x_test = std.transform(x_test)# 逻辑回归预测lg = LogisticRegression(C=1.0)lg.fit(x_train,y_train)print(lg.coef_)y_predict = lg.predict(x_test)print("准确率：",lg.score(x_test,y_test))print("召回率：", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"]))return Noneif __name__ == "__main__":logistic()

输出结果：

     Sample code number  Clump Thickness  ...  Mitoses  Class
0               1000025                5  ...        1      2
1               1002945                5  ...        1      2
2               1015425                3  ...        1      2
3               1016277                6  ...        1      2
4               1017023                4  ...        1      2
..                  ...              ...  ...      ...    ...
694              776715                3  ...        1      2
695              841769                2  ...        1      2
696              888820                5  ...        2      4
697              897471                4  ...        1      4
698              897471                4  ...        1      4
[699 rows x 11 columns]
D:\installed\Anaconda3\lib\site-packages\sklearn\linear_model\logistic.py:432: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.FutureWarning)
[[ 1.48655604 -0.03632439  0.54633716  0.80247214  0.43417113  1.176206031.37521541  0.79215824  0.86304763]]
准确率： 0.9590643274853801
召回率：               precision    recall  f1-score   support良性       0.97      0.97      0.97       117恶性       0.94      0.93      0.93        54accuracy                           0.96       171macro avg       0.95      0.95      0.95       171
weighted avg       0.96      0.96      0.96       171

2.7 逻辑回归的优缺点

优点：
1、实现简单，广泛的应用于工业问题上；
2、分类时计算量非常小，速度很快，存储资源低；
3、便利的观测样本概率分数；
4、对逻辑回归而言，多重共线性并不是问题，它可以结合L2正则化来解决该问题；
5、适合需要得到一个分类概率的场景

缺点：
1、当特征空间很大时，逻辑回归的性能不是很好（看硬件能力）
2、容易欠拟合，一般准确度不太高。
3、不能很好地处理大量多类特征或变量
4、只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分；
5、对于非线性特征，需要进行转换；

2.8 逻辑回归 VS 线性回归

线性回归和逻辑回归是2种经典的算法。经常被拿来做比较，下面整理了一些两者的区别：
在这里插入图片描述
1、线性回归只能用于回归问题，逻辑回归虽然名字叫回归，但是更多用于分类问题
2、线性回归要求因变量是连续性数值变量，而逻辑回归要求因变量是离散的变量
3、线性回归要求自变量和因变量呈线性关系，而逻辑回归不要求自变量和因变量呈线性关系。
4、线性回归可以直观的表达自变量和因变量之间的关系，逻辑回归则无法表达变量之间的关系。

注：
自变量： 主动操作的变量，可以看做“因变量”的原因
因变量： 因为“自变量”的变化而变化，可以看做“自变量”的结果。也是我们想要预测的结果。

2.9 多分类问题

逻辑回归解决办法：1V1,1Vall
在这里插入图片描述

softmax方法-逻辑回归在多分类问题上的推广

打个赏呗，您的支持是我坚持写好博文的动力
在这里插入图片描述

这篇关于15_岭回归-Ridge、岭回归API、线性回归和岭回归的对别；逻辑回归、sigmoid函数、逻辑回归公式、损失函数、逻辑回归API、逻辑回归案例、逻辑回归的优缺点、逻辑回归 VS 线性回归等的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/918175。

相关文章

Ilya-AI分享的他在OpenAI学习到的15个提示工程技巧

Ilya-AI分享的他在OpenAI学习到的15个提示工程技巧

Ilya（不是本人，claude AI）在社交媒体上分享了他在OpenAI学习到的15个Prompt撰写技巧。 以下是详细的内容： 提示精确化:在编写提示时,力求表达清晰准确。清楚地阐述任务需求和概念定义至关重要。例:不用"分析文本",而用"判断这段话的情感倾向:积极、消极还是中性"。 快速迭代:善于快速连续调整提示。熟练的提示工程师能够灵活地进行多轮优化。例:从"总结文章"到"用
阅读更多...
这15个Vue指令，让你的项目开发爽到爆

这15个Vue指令，让你的项目开发爽到爆

1. V-Hotkey 仓库地址: github.com/Dafrok/v-ho… Demo: 戳这里 https://dafrok.github.io/v-hotkey 安装: npm install --save v-hotkey 这个指令可以给组件绑定一个或多个快捷键。你想要通过按下 Escape 键后隐藏某个组件，按住 Control 和回车键再显示它吗？小菜一碟： <template
阅读更多...
Hadoop企业开发案例调优场景

Hadoop企业开发案例调优场景

需求 （1）需求：从1G数据中，统计每个单词出现次数。服务器3台，每台配置4G内存，4核CPU，4线程。 （2）需求分析： 1G / 128m = 8个MapTask；1个ReduceTask；1个mrAppMaster 平均每个节点运行10个 / 3台 ≈ 3个任务（4    3    3） HDFS参数调优 （1）修改：hadoop-env.sh export HDFS_NAMENOD
阅读更多...
性能分析之MySQL索引实战案例

性能分析之MySQL索引实战案例

文章目录 一、前言二、准备三、MySQL索引优化四、MySQL 索引知识回顾五、总结 一、前言 在上一讲性能工具之 JProfiler 简单登录案例分析实战中已经发现SQL没有建立索引问题，本文将一起从代码层去分析为什么没有建立索引？ 开源ERP项目地址：https://gitee.com/jishenghua/JSH_ERP 二、准备 打开IDEA找到登录请求资源路径位置
阅读更多...
深入探索协同过滤：从原理到推荐模块案例

深入探索协同过滤：从原理到推荐模块案例

文章目录 前言一、协同过滤1. 基于用户的协同过滤（UserCF）2. 基于物品的协同过滤（ItemCF）3. 相似度计算方法 二、相似度计算方法1. 欧氏距离2. 皮尔逊相关系数3. 杰卡德相似系数4. 余弦相似度 三、推荐模块案例1.基于文章的协同过滤推荐功能2.基于用户的协同过滤推荐功能 前言     在信息过载的时代，推荐系统成为连接用户与内容的桥梁。本文聚焦于
阅读更多...
hdu1171（母函数或多重背包）

hdu1171（母函数或多重背包）

题意：把物品分成两份，使得价值最接近 可以用背包，或者是母函数来解，母函数（1 + x^v+x^2v+.....+x^num*v）（1 + x^v+x^2v+.....+x^num*v）（1 + x^v+x^2v+.....+x^num*v） 其中指数为价值，每一项的数目为（该物品数+1）个 代码如下： #include<iostream>#include<algorithm>
阅读更多...
Android平台播放RTSP流的几种方案探究（VLC VS ExoPlayer VS SmartPlayer）

Android平台播放RTSP流的几种方案探究（VLC VS ExoPlayer VS SmartPlayer）

技术背景 好多开发者需要遴选Android平台RTSP直播播放器的时候，不知道如何选的好，本文针对常用的方案，做个大概的说明： 1. 使用VLC for Android VLC Media Player（VLC多媒体播放器），最初命名为VideoLAN客户端，是VideoLAN品牌产品，是VideoLAN计划的多媒体播放器。它支持众多音频与视频解码器及文件格式，并支持DVD影音光盘，VCD影
阅读更多...
【区块链 + 人才服务】可信教育区块链治理系统 | FISCO BCOS应用案例

【区块链 + 人才服务】可信教育区块链治理系统 | FISCO BCOS应用案例

伴随着区块链技术的不断完善，其在教育信息化中的应用也在持续发展。利用区块链数据共识、不可篡改的特性， 将与教育相关的数据要素在区块链上进行存证确权，在确保数据可信的前提下，促进教育的公平、透明、开放，为教育教学质量提升赋能，实现教育数据的安全共享、高等教育体系的智慧治理。 可信教育区块链治理系统的顶层治理架构由教育部、高校、企业、学生等多方角色共同参与建设、维护，支撑教育资源共享、教学质量评估、
阅读更多...
客户案例：安全海外中继助力知名家电企业化解海外通邮困境

客户案例：安全海外中继助力知名家电企业化解海外通邮困境

1、客户背景 广东格兰仕集团有限公司（以下简称“格兰仕”），成立于1978年，是中国家电行业的领军企业之一。作为全球最大的微波炉生产基地，格兰仕拥有多项国际领先的家电制造技术，连续多年位列中国家电出口前列。格兰仕不仅注重业务的全球拓展，更重视业务流程的高效与顺畅，以确保在国际舞台上的竞争力。 2、需求痛点 随着格兰仕全球化战略的深入实施，其海外业务快速增长，电子邮件成为了关键的沟通工具。
阅读更多...
【区块链 + 人才服务】区块链集成开发平台 | FISCO BCOS应用案例

【区块链 + 人才服务】区块链集成开发平台 | FISCO BCOS应用案例

随着区块链技术的快速发展，越来越多的企业开始将其应用于实际业务中。然而，区块链技术的专业性使得其集成开发成为一项挑战。针对此，广东中创智慧科技有限公司基于国产开源联盟链 FISCO BCOS 推出了区块链集成开发平台。该平台基于区块链技术，提供一套全面的区块链开发工具和开发环境，支持开发者快速开发和部署区块链应用。此外，该平台还可以提供一套全面的区块链开发教程和文档，帮助开发者快速上手区块链开发。
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2