本文主要是介绍DL_Classification、Logistic Regression、Deep Intro_Day4,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- Classification
- two classes
- probability from class
- Gaussian Distribution
- Maximum Likelihood
- Modifying Model
- Logistic Regression
- function set
- evaluation
- find the best function
- multi-class classification
- limitation
- Brief Introduction of DL
- neural network
- goodness of function
- total loss
- gradient descent
- backpropagation
Classification
two classes
二分类的问题:某个东西放在两个类别中的概率各为多少
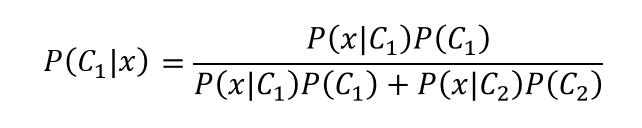
取出一个x,它属于C1的概率。
probability from class
Gaussian Distribution
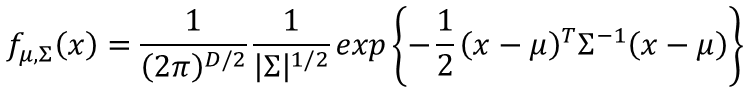
这里输出是某个x的概率,的μ是所有x样本的均值,的∑为是方差矩阵。
上面公式的图形分布如下所示:想象一下三维的高斯分布

Maximum Likelihood
极大似然估计(各项独立同分布)
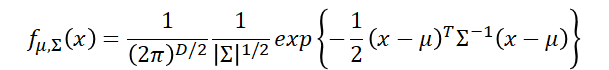
要使这些样本都属于这个分布的概率最大,也就是下式要最大。
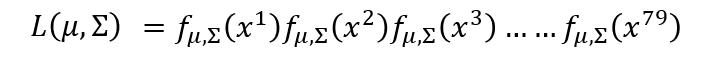
所以我们需要求它的最大值:已知条件如下

我们就用以上的条件,和之前二分类的公式(多分类就贝叶斯公式)来训练模型:
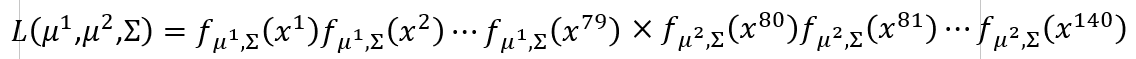
Modifying Model
在一长串的数学计算之后,我们可以得到下面的模型。也就是可以训练的w和b。

Logistic Regression
function set
用线性回归的方式来求解分类问题,这里我们可以认为。大于0.5的认为是1,小于0.5的认为是0,从而实现二分类。
核函数如下图右边和左边底下所示 sigmoid function

下图是W与x乘积的示意图:

evaluation
我们先假设分类如下图所示:
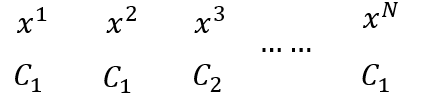
我们来写出它的预测好坏的概率公式,默认函数f为分布在C1上的概率,则他们分布正确的总概率为:
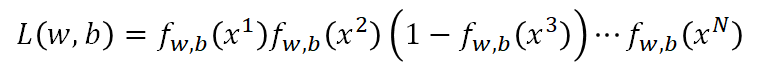
这样我们就要找到合适的W,b是这个方程最大
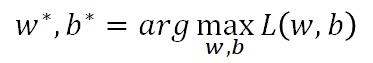
通过上面假定,我们可以设置损失函数如下所示:
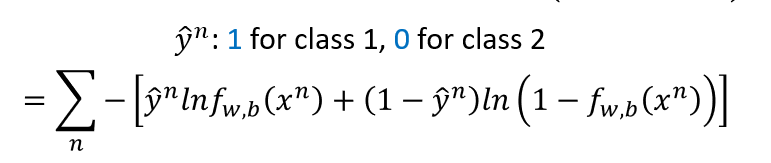
find the best function
又是在一堆复杂的计算之后:
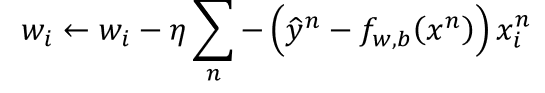
逻辑回归和线性回归的区别

multi-class classification
多元的分类,可以先利用权重系数对输入的值进行处理,使得其输出类似于one-hot编码

limitation
因为逻辑回归分类本质上还是在平面中画一条线将不同的区域分割开,但有很多情况这些分类是不能用直线划分出区别的。
比如下面的分类,我们直接用逻辑回归就分不开。

这时候,我们可以通过类似变换坐标轴的方式(乘上一个矩阵在加上b)类似这样。这种方式其实就是神经网络中把变量训练到隐含层中。

Brief Introduction of DL
neural network
其实就是和上文中类似的将旧的变量,变成新的变量。在经过多次这样的训练后,其形状类似网络,就可以叫做神经网络。

goodness of function
在最后训练出来的预测值,与实际值之间按照逻辑回归中损失函数的计算方式来表示训练结果的好坏。

total loss
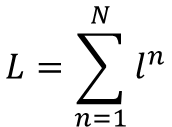
gradient descent
通过每一步损失函数来得出下降的梯度。

backpropagation
反向传播是计算𝜕𝐿∕𝜕𝑤的有效途径,之后会详细讲述。
这篇关于DL_Classification、Logistic Regression、Deep Intro_Day4的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






