本文主要是介绍NLP10_逻辑回归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

逻辑回归是经典的baseline

要想通过线性回归来表示概率,那概率必须是(0,1)范围,但是显然等式右边是负无穷到正无穷的范围

逻辑函数
使用逻辑函数作为激活函数
通过sigmoid函数,把条件概率的值限定在0-1的范围
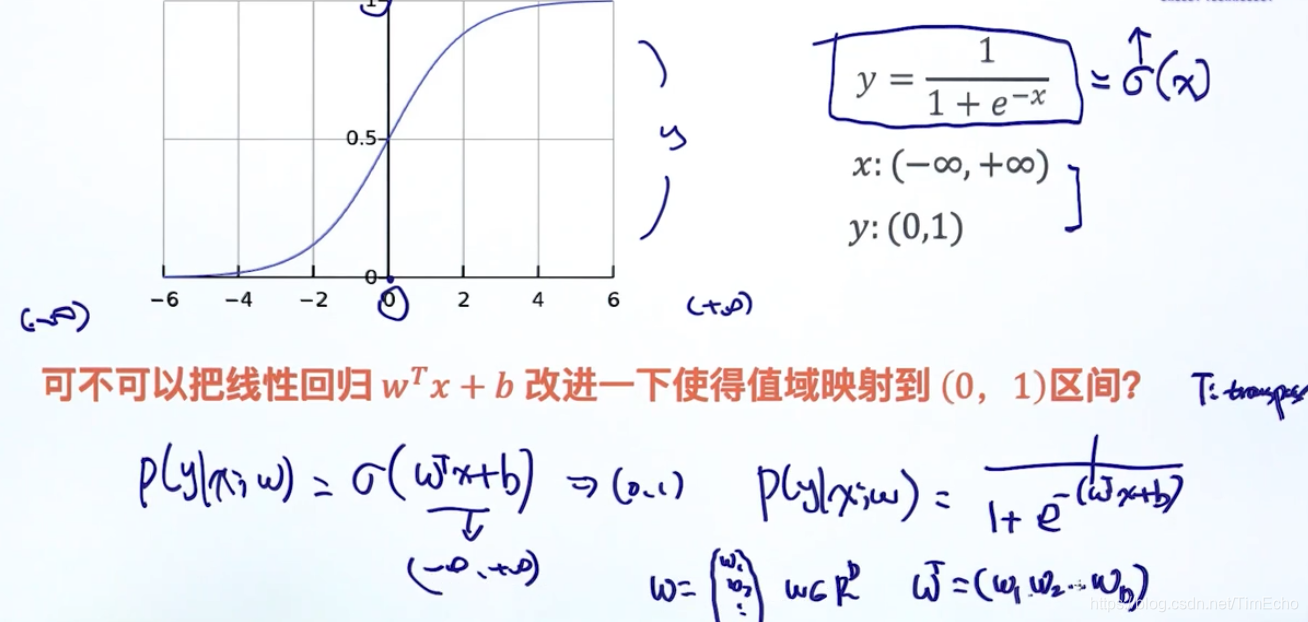
原始条件概率的范围是不符合概率的定义的,所以要经过逻辑函数,也就是这里用的sigmoid函数,将其概率的范围修改为0-1,满足了概率的定义
通过训练已有的数据,得到参数w和b,这样我将特征x输入,经过激活函数处理,就可以得到一个概率

二分类条件概率
将两个分类写到一个公式

逻辑回归是线性的分类器
判断是线性还是非线性,是看他最终的训练后的一个决策边界,
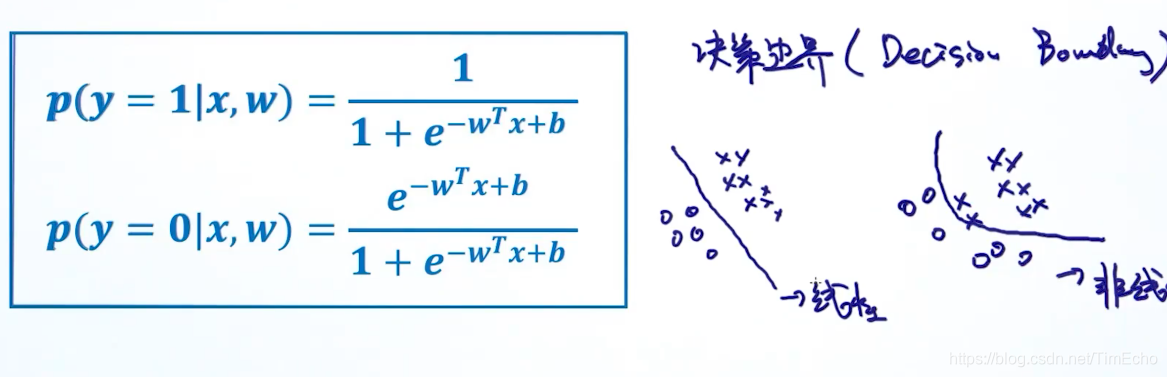
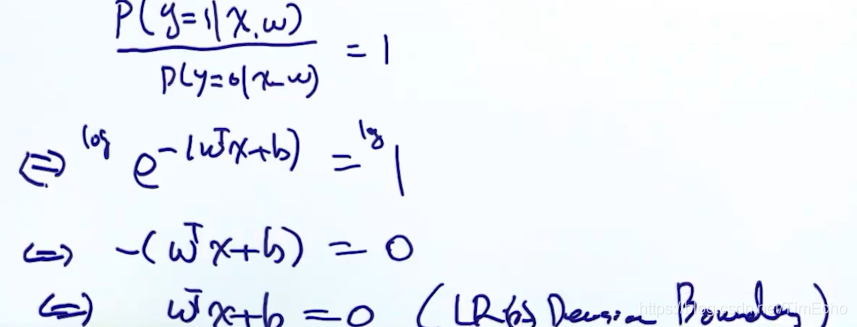
因为落在边界上的点既可以属于0分类,也可以属于1分类,也就是属于0还是属于1的概率相同,即概率比值为1,由上式证明可知,逻辑回归是线性的
当数据是线性可分的,那么参数w会趋近于无穷大、
原因:要达到分类的效果,我们希望条件概率y=1越大越好,或者y=0越大越好。
假如我是正样本,那么y=1的条件概率我希望是趋向于1,那么此时e的指数这一项趋近于0,推出wx+b这一项趋向于无穷大,
也就是w趋向于无穷大,w是这个回归方程的系数,所以w无穷大对应的就是垂直于x轴的那条分割线
同样,,假如是负样本,w也是无穷大
这其实就是一个过拟合的问题
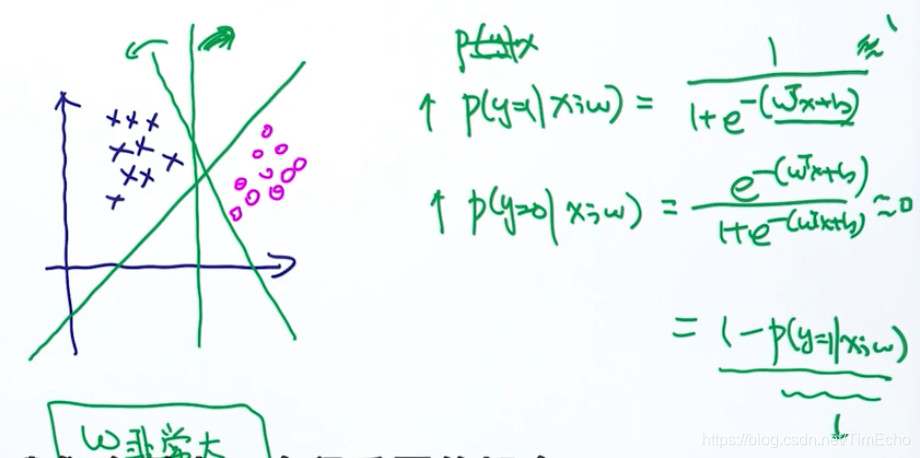
如何避免w无穷大呢?
L2 Norm,控制参数不要变的特别大
在原来的目标函数的基础上加了一个正则项,来调节w
λ是超参数,它为0,w无限制
λ大的时候,w变的更小,它小的时候,w变的更大,达到了调节w的目的

为了选择合适的λ,一般会使用交叉验证来选出
简单模型可以更好避免过拟合
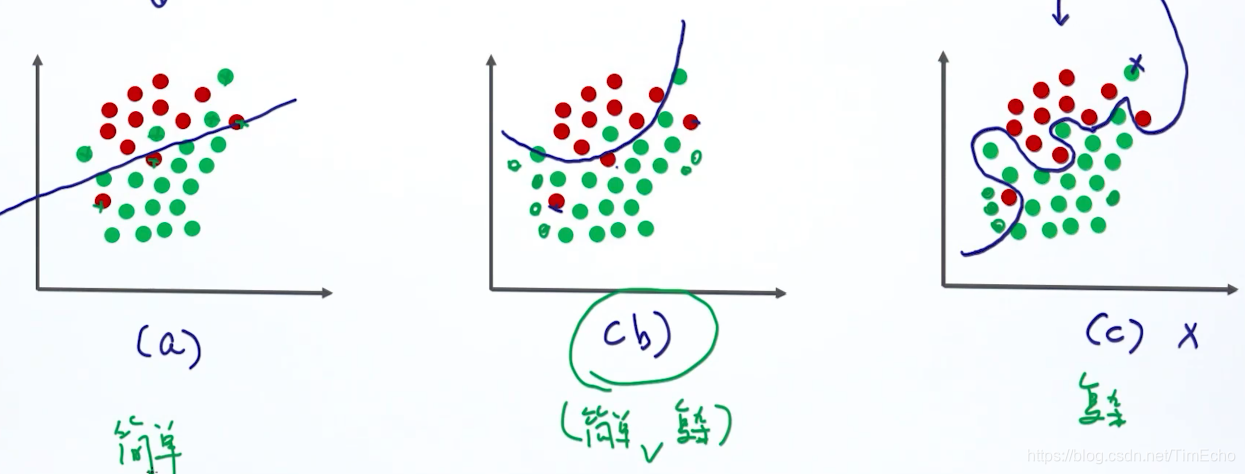
泛化能力
我们要的是训练集上训练出来的模型,在测试集中也有很好的表现。
泛化能力越好,那么我的模型复杂度可能变高,泛化能力差,就会产生过拟合的现象。所以我们要选择一个复杂度适中,泛化能力又好的模型
模型复杂度
发生过拟合现象的四个原因:
1、模型的选择:简单模型适合用于简单环境,复杂模型用于复杂环境,简单模型有LR、SVM
2、参数个数:减少参数个数
3、参数空间的选择:正则的作用就是从参数空间中选择出简单的参数空间,加正则项
4、拟合过少的样本:获取更多样本
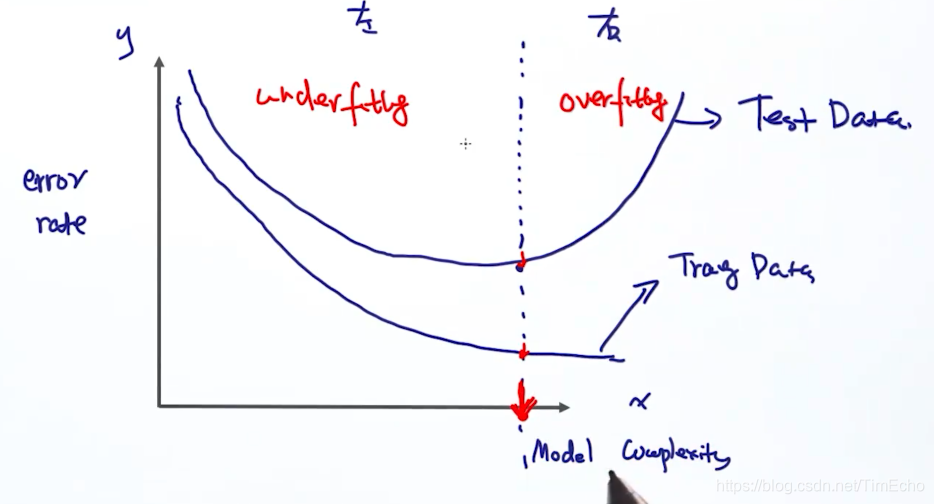
如图,x轴为模型复杂度,y为错误率
可以看出,到达红线处,测试集中的错误率最低,
而在红线左边,模型复杂度低,错误率也比较高,这是错误率还是可以通过增加模型复杂度来降低的,这是欠拟合
而在红线右边,模型复杂度继续增加,测试集上的表现却开始变差,错误率变高,这就是过拟合
我们要找到那个测试集上错误率最低的点时的模型复杂度,确定这个模型是最好的模型
正则
L2 Norm

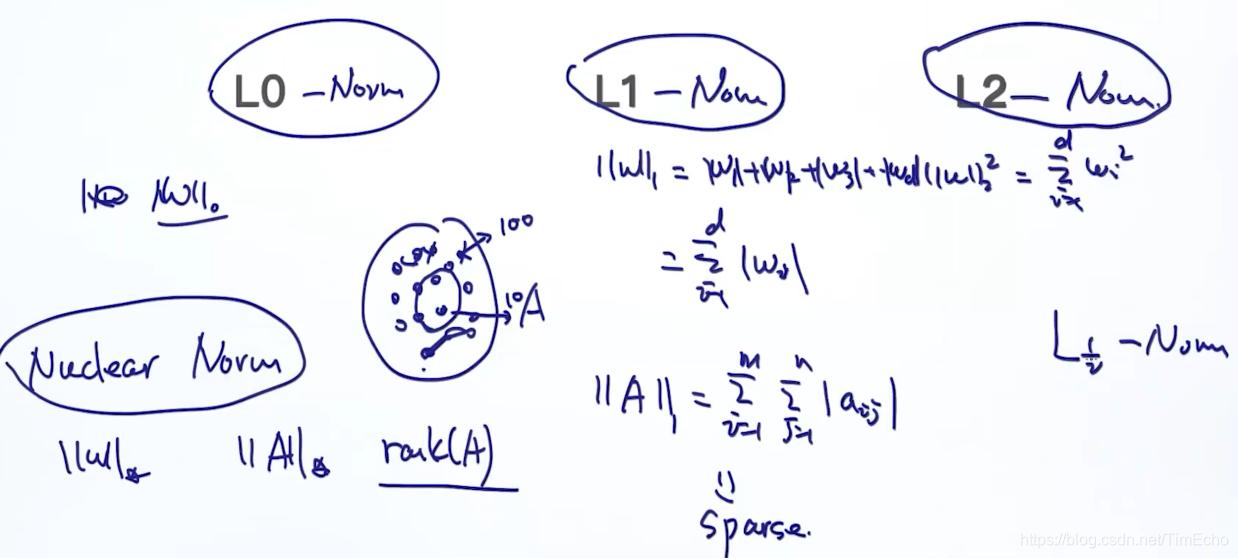
还有不同的范数用在正则项,
L1 Norm计算的是绝对值和
L2计算的是平方和
L1和L2都会控制参数w,使其不会变得太大
L1Norm存在稀疏性,经常用于将很多参数变为0,遇到跟稀疏相关的模型,会用到L1Norm
Nuclear norm:用于去除矩阵中很大的那些秩
这篇关于NLP10_逻辑回归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









