本文主要是介绍多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法 学习记录01——数学基础,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
系列文章目录
本科毕设正在做多轴机械臂相关的内容,这里是一个学习机械臂运动学课程的相关记录。
如有任何问题,可发邮件至layraliu@foxmail.com问询。
1. 数学基础
文章目录
- 系列文章目录
- 一、空间位置、姿态描述
- 二、旋转矩阵(Rotation matrix)
- 1.特性
- 2.用法
- 3.旋转矩阵与转角(旋转的前后顺序不能互换)
- 三、变换矩阵
- 1.如何将移动和转动整合在一起
- 2.transformation matrix运算
- 总结
一、空间位置、姿态描述
- 运动学建模分类
正运动学:根据协作机器人的关节角度,计算末端位姿。
逆运动学:已知机器人末端位置,反解其关节角,涉及多解问题。 - 空间某点位置
3 x 1的位置矢量
空间点p=[x0 y0 z0]T(列向量) - 一个刚体的姿态如何描述
平面:移动2 DOFs(degree of freedom)、转动1 DOFs(两个面一个转动,c22=1)
空间:移动3 DOFs(degree of freedom)、转动3 DOFs(两个面一个转动,c32=3)
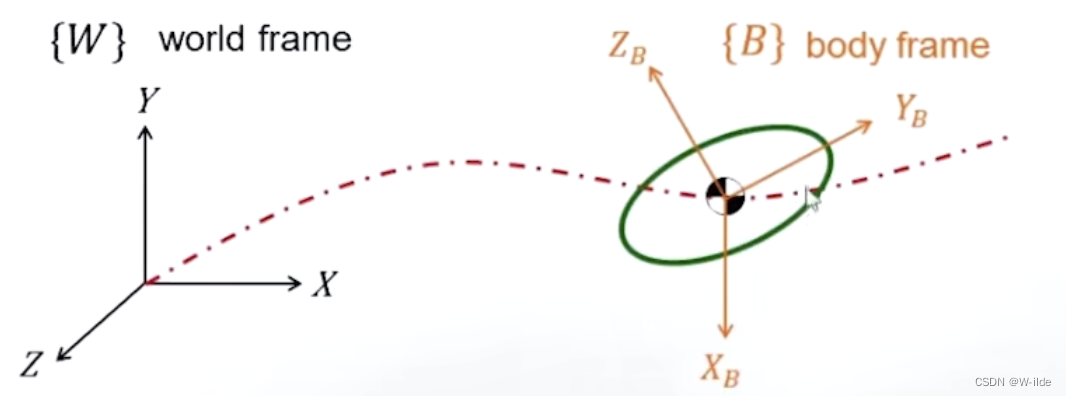
由上图可知(红色为刚体质心随时间变化的轨迹),刚体的移动由body frame的原点位置判定;刚体的转动由body frame的姿态判定。
利用各个DOF的微分/二次微分,将位移和姿态转换到速度和加速度的运动状态。 - 转动(旋转矩阵)
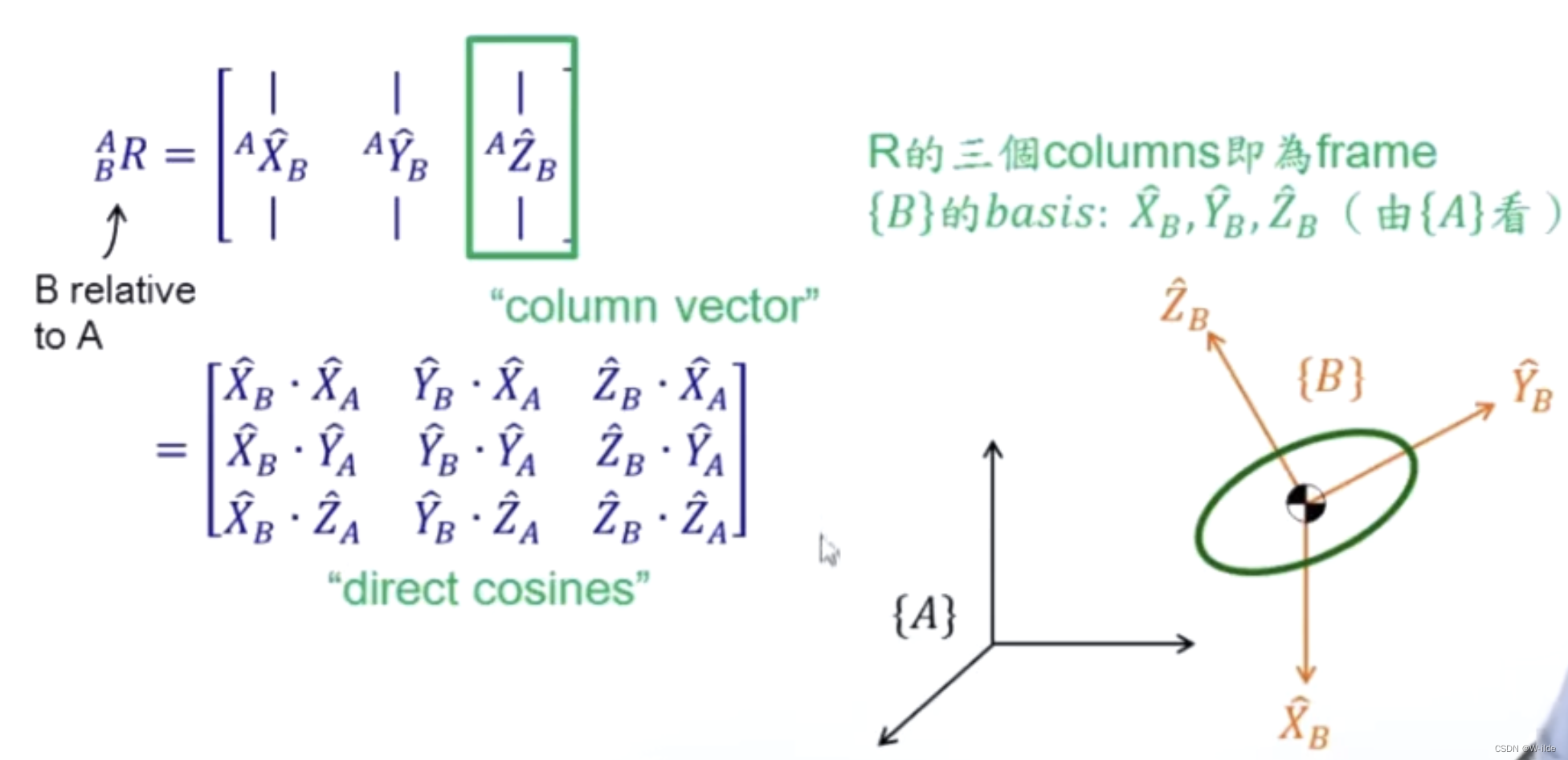
描述B相对于A的姿态。(觉得湾湾翻译不太一样哈哈哈,其中direct cosines应为direction cosines?我理解就是方向余弦)
那其实也可以很显然的发现,旋转矩阵是一个正交矩阵。其每一列都是单位矩阵,并且两两正交(坐标轴不就是互相垂直的嘛)。
二、旋转矩阵(Rotation matrix)
1.特性
(其实就是正交矩阵的转置亦为其逆)


其实此矩阵的秩=3(阶数),所以转动具有3个DOFs。
2.用法
-
描述一个frame相对于另外一个frame的姿态
-
将point由某个frame的表达,转换到另一个frame。(可以联想一下线代里面有关于基向量那部分的知识,同一个向量在不同坐标系中的表达)
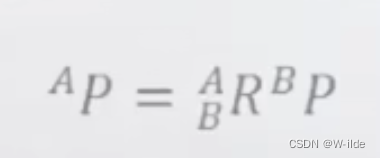
-
将point在同一个frame中进行转换。

3.旋转矩阵与转角(旋转的前后顺序不能互换)
- 两个拆解方式
Fixed angles:对方向固定不动的转轴旋转;
Euler angles:对转动的frame当下所在的转轴方向旋转。 - 把旋转矩阵所表达的姿态,拆解成3次旋转角度需注意:
多次旋转的先后顺序需定义;
旋转转轴需要明确定义。 - 对应于绕x,y,z轴旋转θ角度的位姿变化,对应的旋转矩阵分别为:(逆时针为正方向)
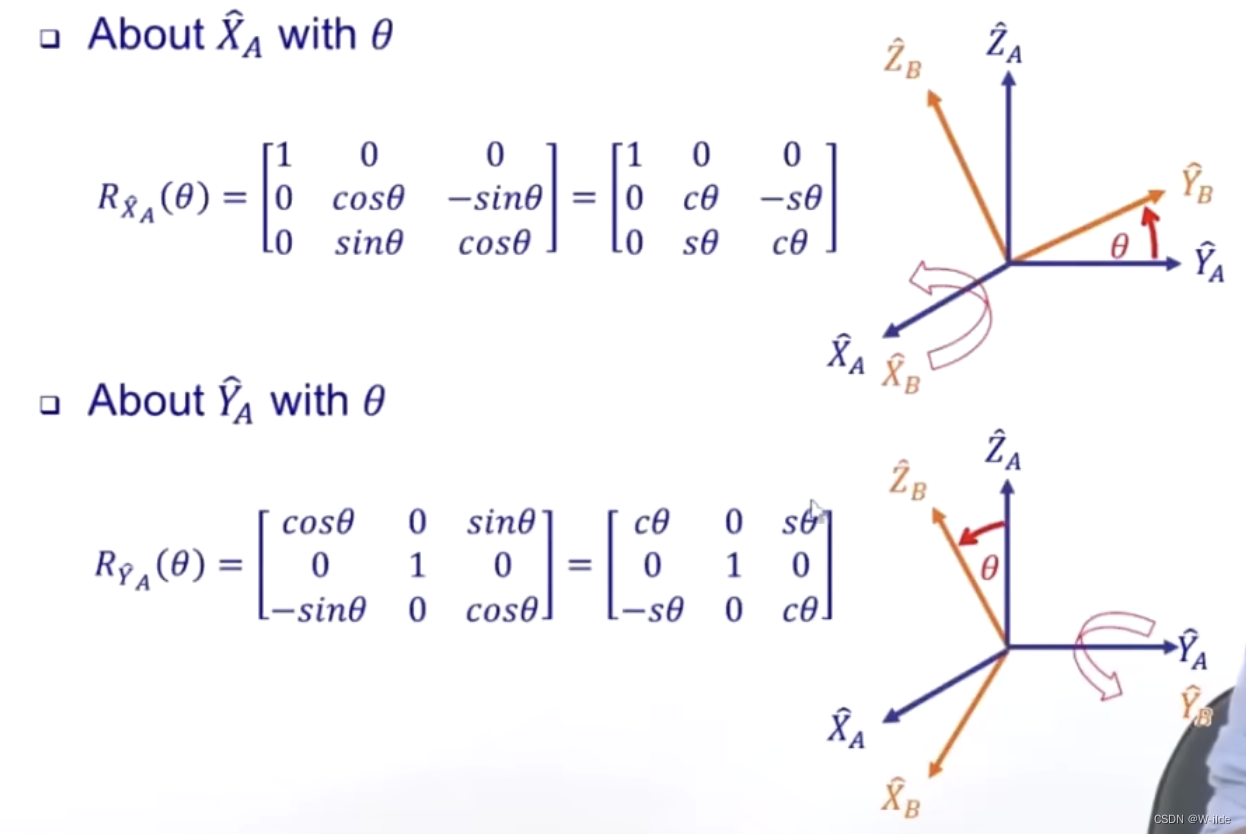
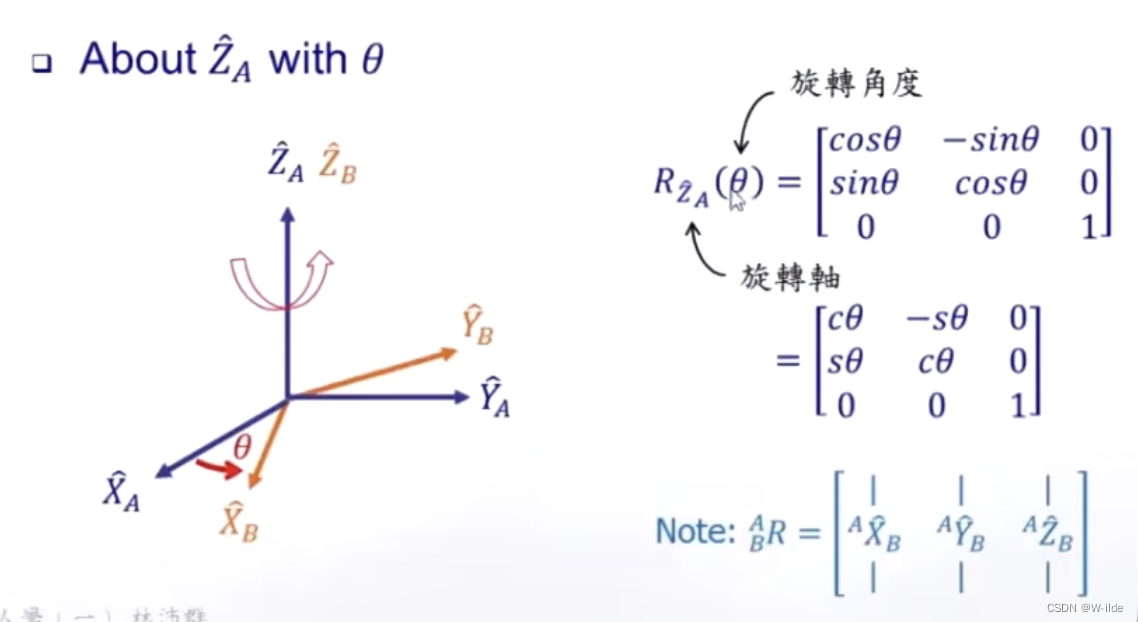
- Fixed angles(按照x——y——z顺序转)
已知各轴分别较之Fixed angles的旋转角度,如何推算旋转矩阵?
(新变换要左乘)
已知旋转矩阵,如何推算各轴分别较之Fixed angles的旋转角度?
注意:atan2是一个函数,在C语言里返回的是指方位角,C 语言中atan2的函数原型为 double atan2(double y, double x) ,返回以弧度表示的 y/x 的反正切。y 和 x 的值的符号决定了正确的象限。也可以理解为计算复数 x+yi 的辐角,计算时atan2 比 atan 稳定。

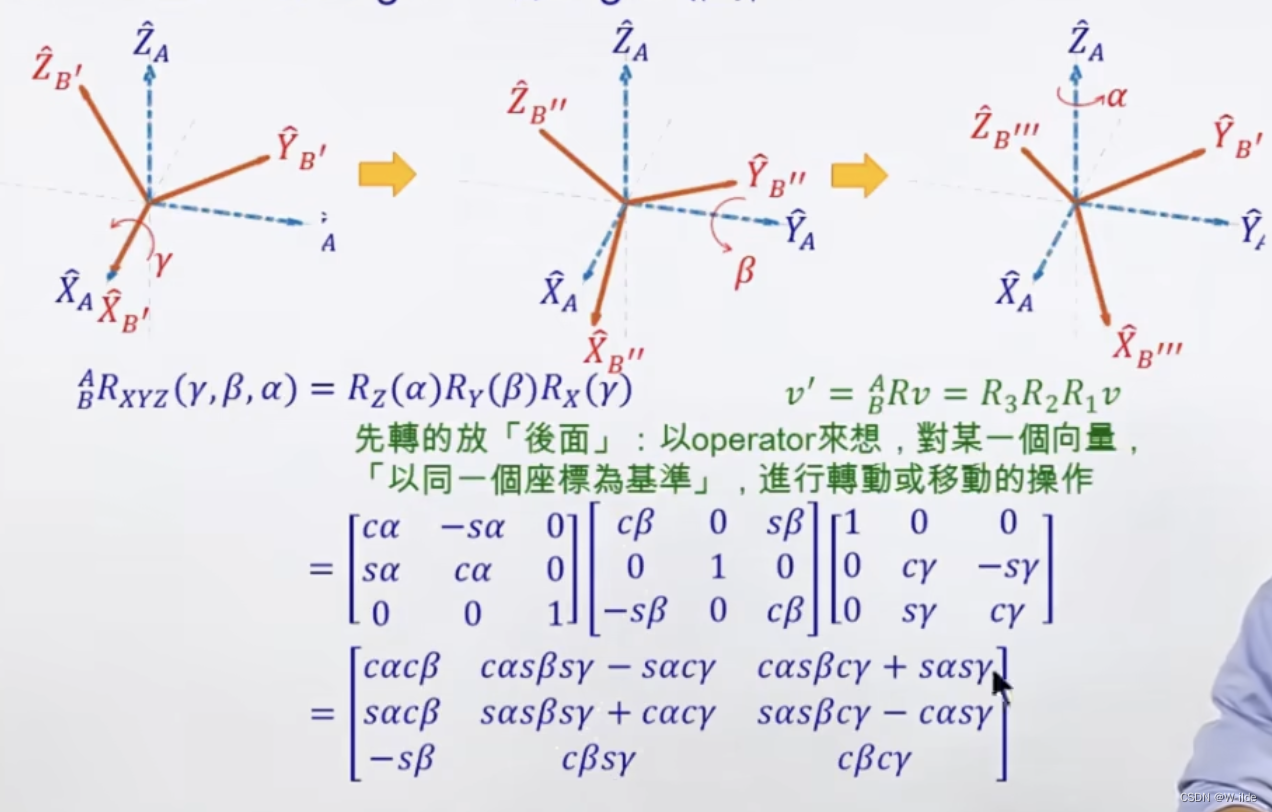
- Euler angles(按照z——y——x顺序转)
(新变换要右乘,其实就是绝对坐标左乘,相对坐标右乘)这样就保证了,虽然Euler和fixed angles变换的转轴不一致,但仍能得到相同的公式。
已知各轴分别较之Fixed angles的旋转角度,如何推算旋转矩阵?

已知旋转矩阵,如何推算各轴分别较之Fixed angles的旋转角度?

- Euler/Fixed angles
三次转动共有322=12个拆解方法(只要前后两个不一致即可)
Euler正转和Fixed angles反转是有一致性的。 - Angle-axis表达法
- Quaternion表达法(四元素法)

三、变换矩阵
1.如何将移动和转动整合在一起
Homogenous transformation matrix
(以下为mapping角度)
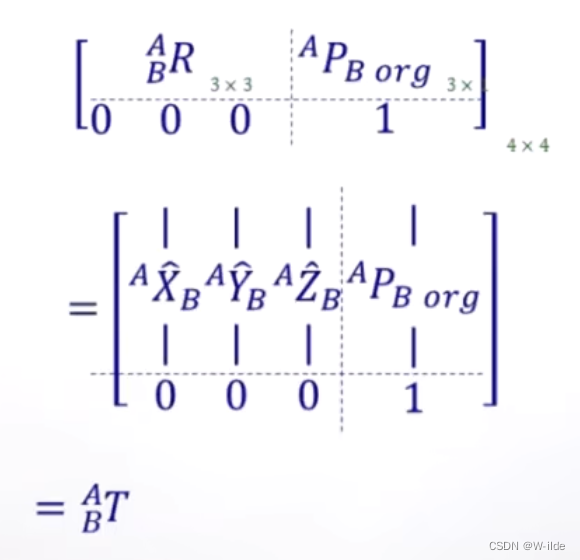
以下图片为Homogenous transformation matrix的证明:(org为B原点)
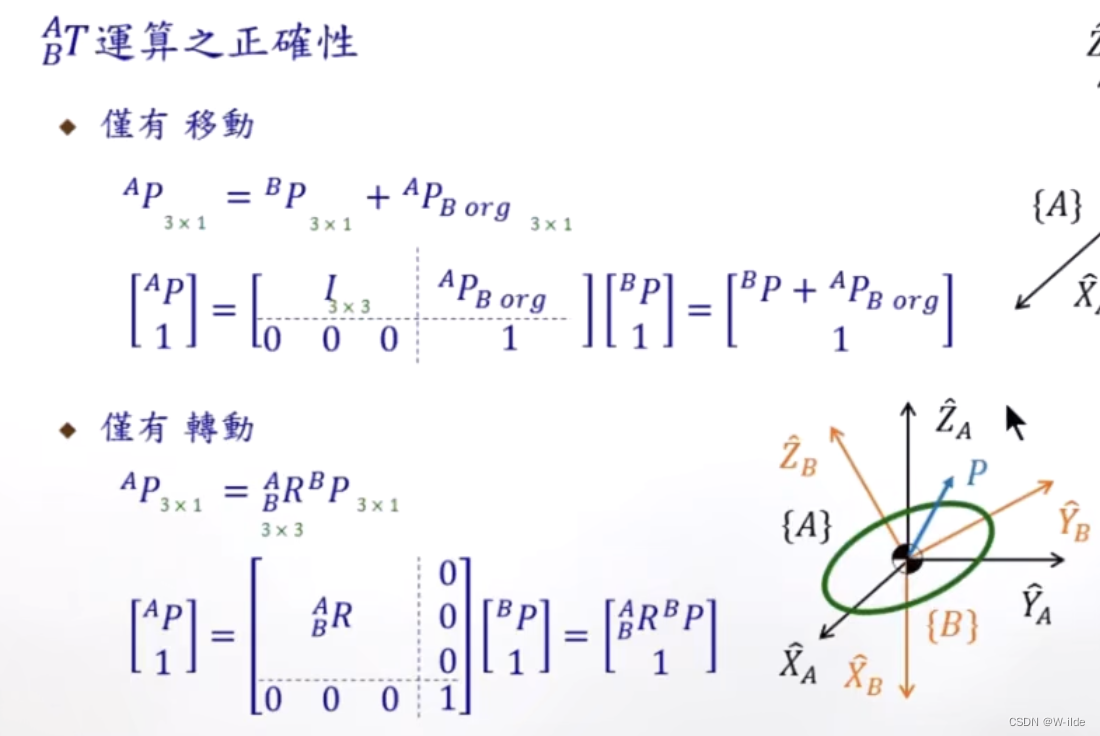
并且可以做连乘

(以下为operator角度)
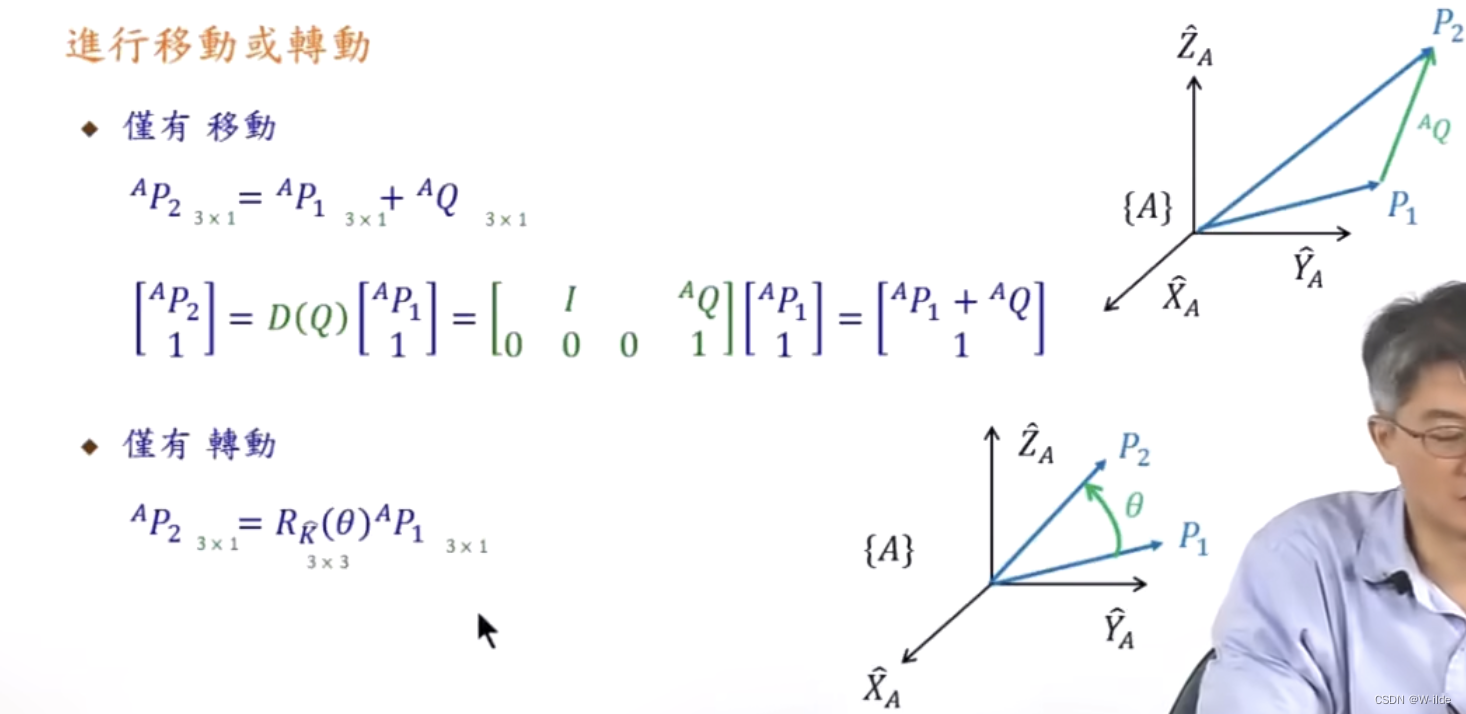
(先转动再移动)
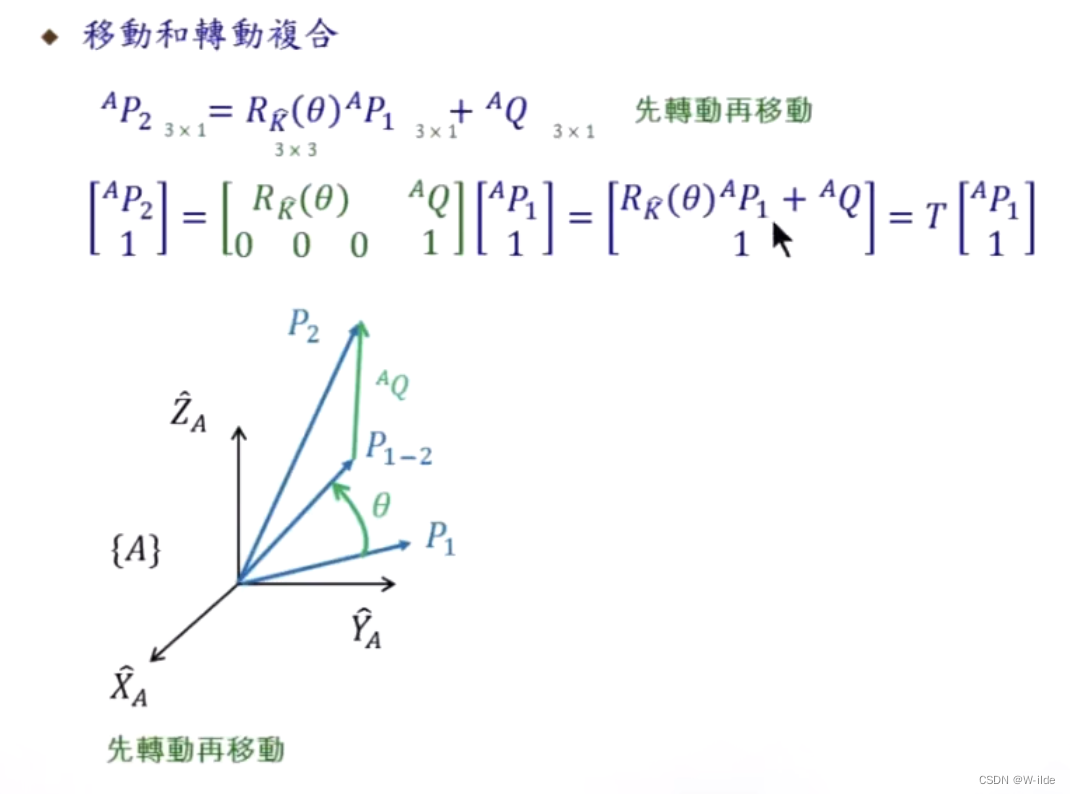
其实可见,移动是加法,转动是乘法。
以下是对两个的理解:
Operators: mapping理解为定位(本身不动,将point由某个frame的表达换到另一个frame来表达),operator理解为变换(本身变了,将point在同一个frame中进行移动和转动)
operator只有一个坐标系,mapping是在二个或多个坐标系。
也就是说对于一个旋转矩阵(我们的本质需求),我们有两种理解方式,一种是线性代数几何应用的Operation,一种是矩阵分析中过渡矩阵的mapping。(来源:)
因为运动是相对的,所以当Homogenous transformation matrix当operator时对向量/点进行移动或转动的操作,也可以想象成是对frame进行反向的。即为point向前/顺时针移,frame往后/逆时针移。
2.transformation matrix运算
-
连续运算
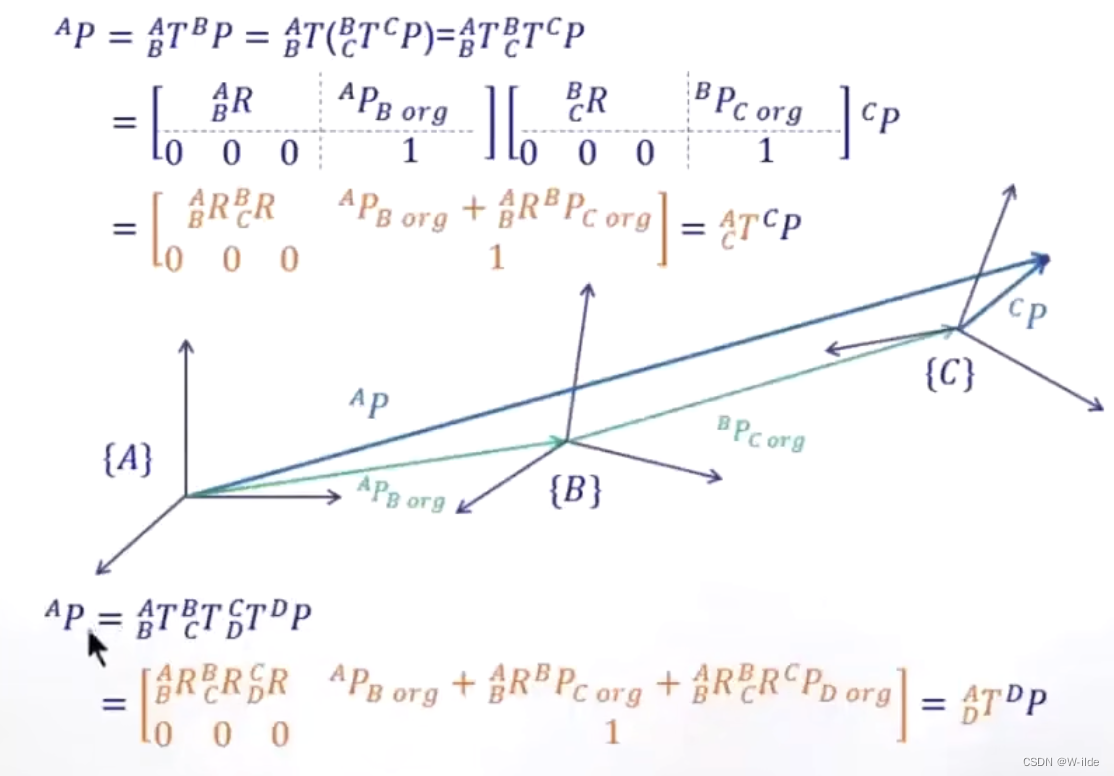
-
反矩阵
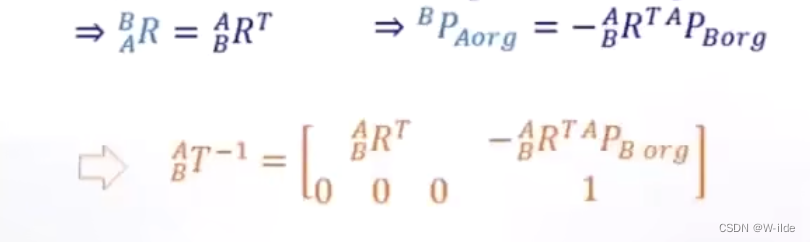
-
连续运算,求未知之相对关系
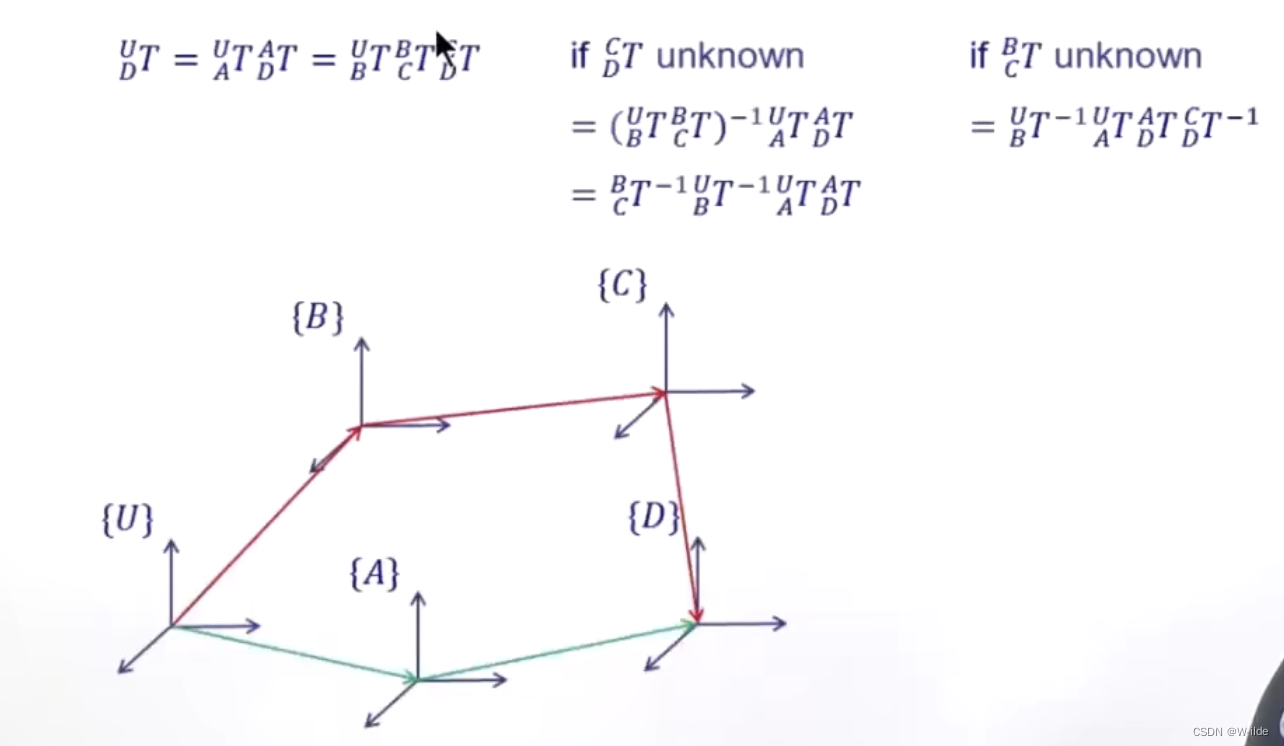
-
连续运算法则
mapping可以理解为映射,而operator可以理解为变化。
总结
以上就是今天要讲的内容,本文仅仅简单介绍了 多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法的学习记录01——数学基础,而Matlab提供了大量能使我们快速便捷地处理数据的函数和方法。如有任何问题,可发邮件至layraliu@foxmail.com问询。
这篇关于多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法 学习记录01——数学基础的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






