本文主要是介绍基于PID-UKF/AUKF锂电池SOC估计,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
(1)对UKF进行改进,引入PID控制器
参考文献:https://doi.org/10.1155/2021/6665509
模型:Thevenin模型
电池类型:钴酸锂
工况:DST工况和FUDS工况
MATLAB版本:R2021b
在这篇参考文献的基础上,对UKF进行改进,引入PID控制思想,对锂电池SOC进行估计。整体思路和PID-EKF是一致的,换汤不换药。
关于PID-EKF/AEKF可以看这篇博客:PID-EKF/AEKF
自适应更新准则如下图所示,仅更新过程噪声误差协方差矩阵Q。
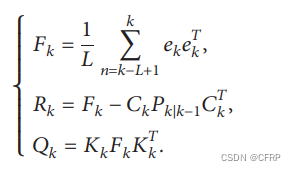
(2)估计结果,以DST工况为例
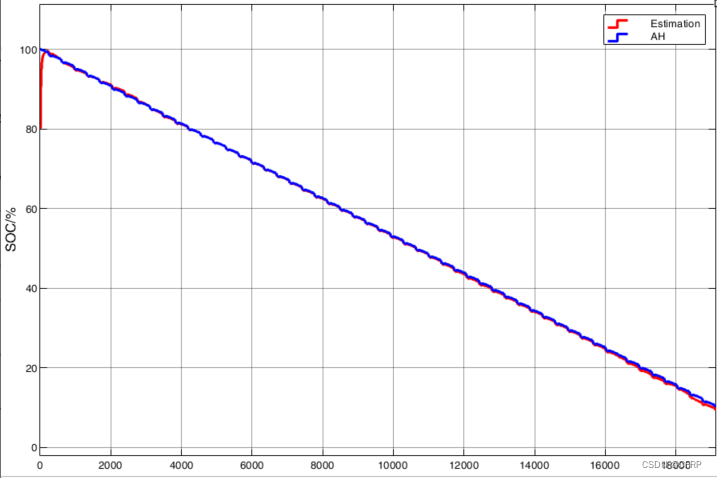
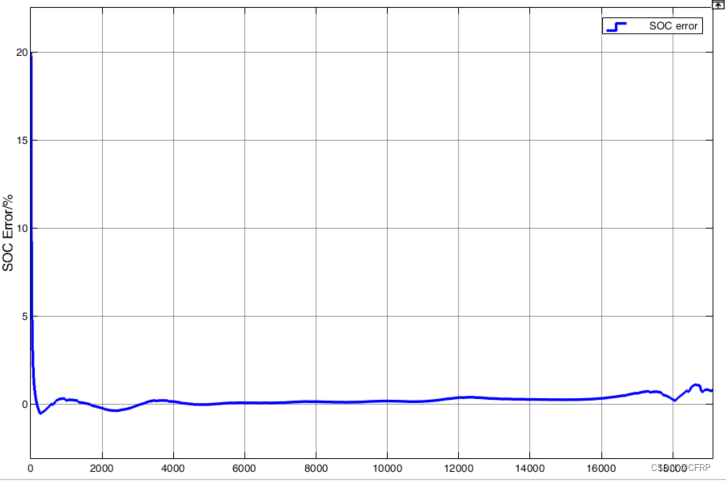
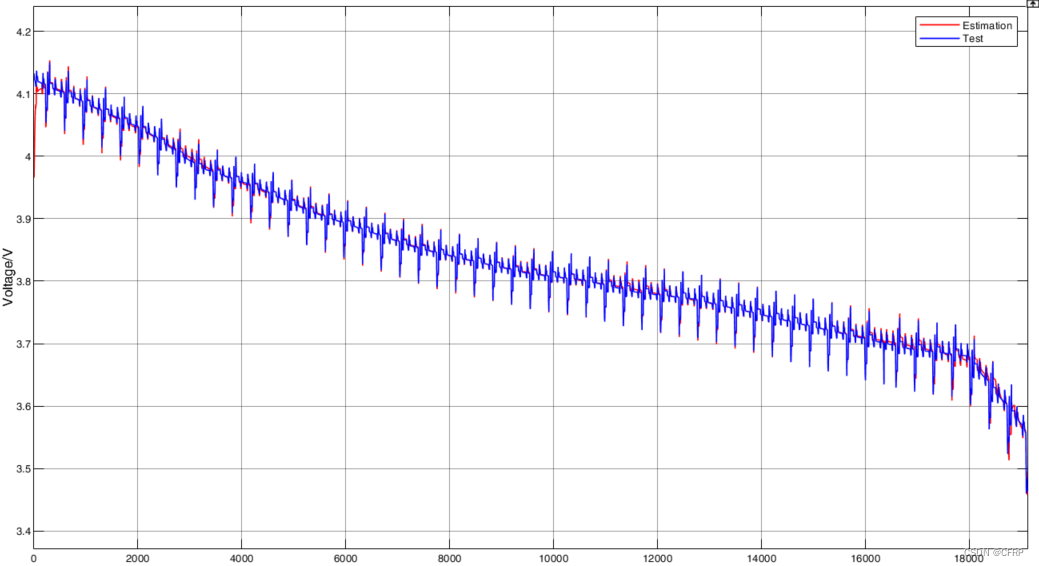
1)PID-UKF估计结果
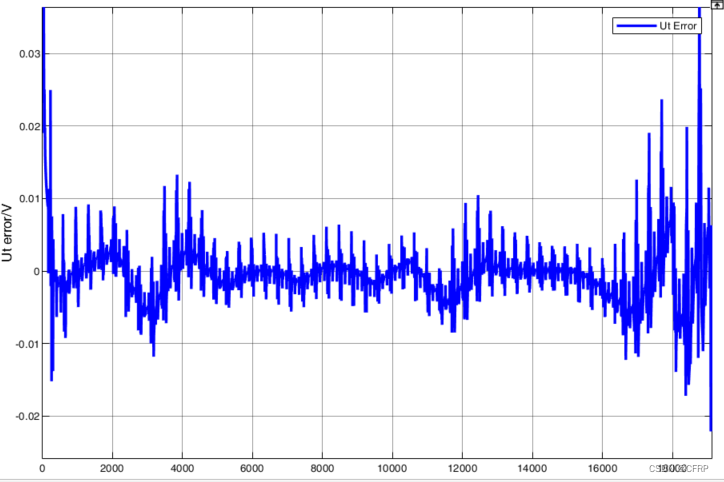
2)PID-AUKF估计结果
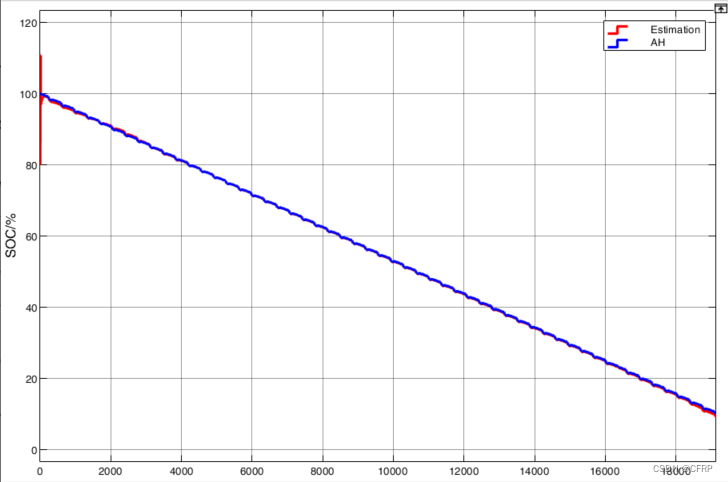
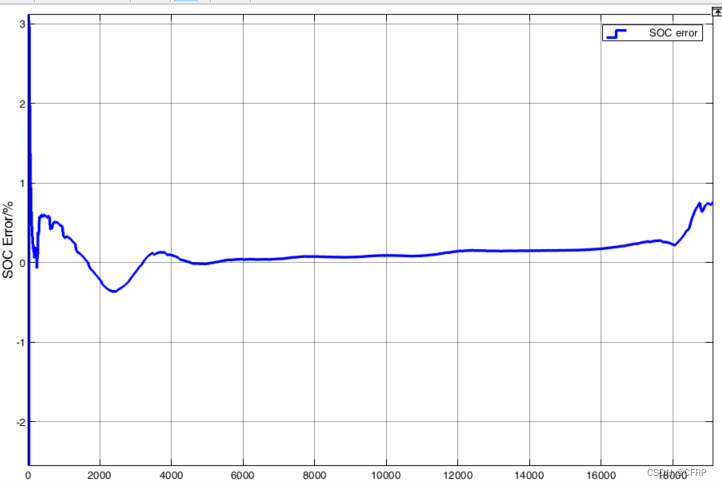
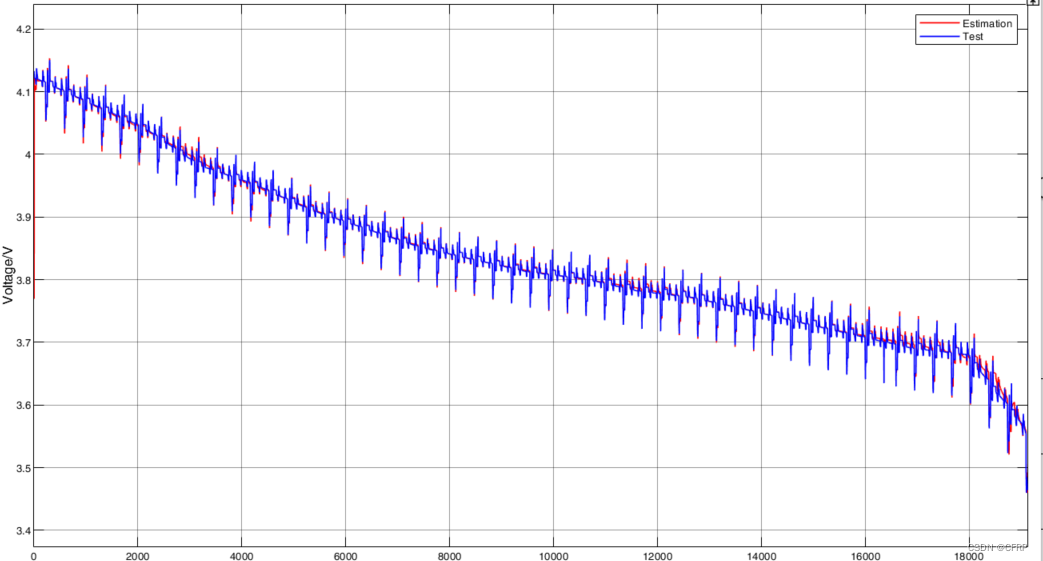
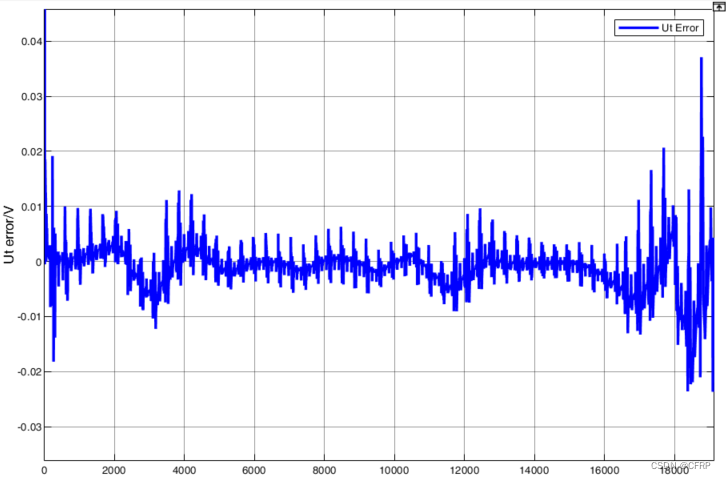
(3)总结
1)在PID-EKF中,模型参数采用拟合查表确定,SOC和端电压估计误差指标为:
SOC
RMSE = 0.7111%
MAE = 0.4717%
端电压
RMSE = 23.0853mv
MAE = 1.011mv
2)在PID-AEKF中,模型参数采用拟合查表确定,SOC和端电压估计误差指标为:
SOC
RMSE = 0.3890%
MAE = 0.1399%
端电压
RMSE = 23.4890mv
MAE = 2.9598mv
3)在PID-UKF中,模型参数在线辨识确定,SOC和端电压估计误差指标为:
SOC
RMSE = 0.5939%
MAE = 0.2713%
端电压
RMSE = 5.459mv
MAE = 2.43mv
4)在PID-AUKF中,模型参数在线辨识确定,SOC和端电压估计误差指标为:
SOC
RMSE = 0.3244%
MAE = 0.1724%
端电压
RMSE = 5.095mv
MAE = 2.494mv
综合估计误差指标可以看出,四种算法各有优越性,且估计算法和协方差矩阵初始值关系密切。因此在比对不同算法优越性的时候,难免会存在因初始值取值偏差得出不一样的结论,因为我们始终无法确定真实误差和噪声到底为多少。在SOC估计中,采取更有说服力和客观的方法确定误差协方差矩阵初始值貌似目前没有太多论文提及和探讨过,一般都是人为直接试凑确定。
这篇关于基于PID-UKF/AUKF锂电池SOC估计的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






