本文主要是介绍Uniformer: Unified Transformer for Efficient Spatial-Temporal Representation Learning，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Unified Transformer for Efficient Spatial-Temporal Representation Learning
- 1. Motivation
- 2. Method
- 2.1 MHRA：
- 2.2 DPE
- 2.3 FFN
1. Motivation
高维视频具有大量的局部冗余和复杂的全局依赖关系，而该研究主要是由3D卷积神经网络和视觉Transformer驱动。3D卷积虽然能抑制局部冗余，但由于接受域有限，它缺乏捕获全局依赖的能力；视觉Transformer在self-attention的帮助下擅长捕捉全局依赖，但由于各层token之间存在盲目相似性比较，限制了减少局部冗余。
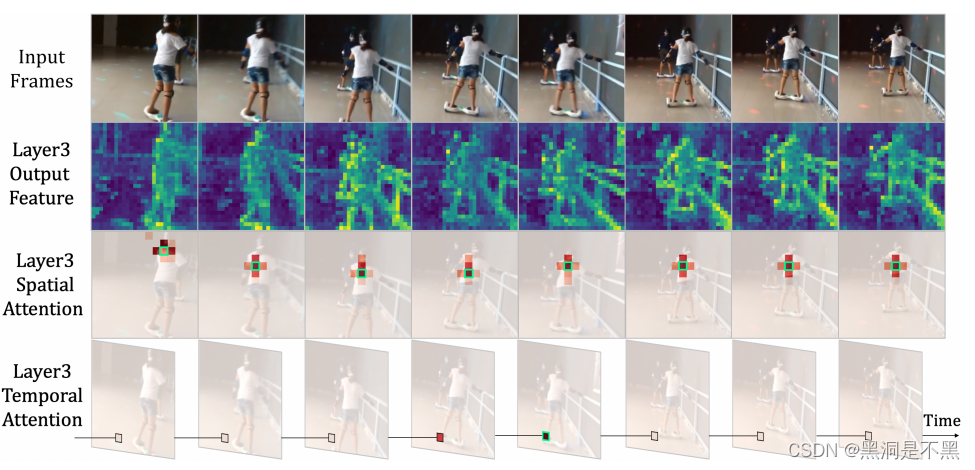
2. Method
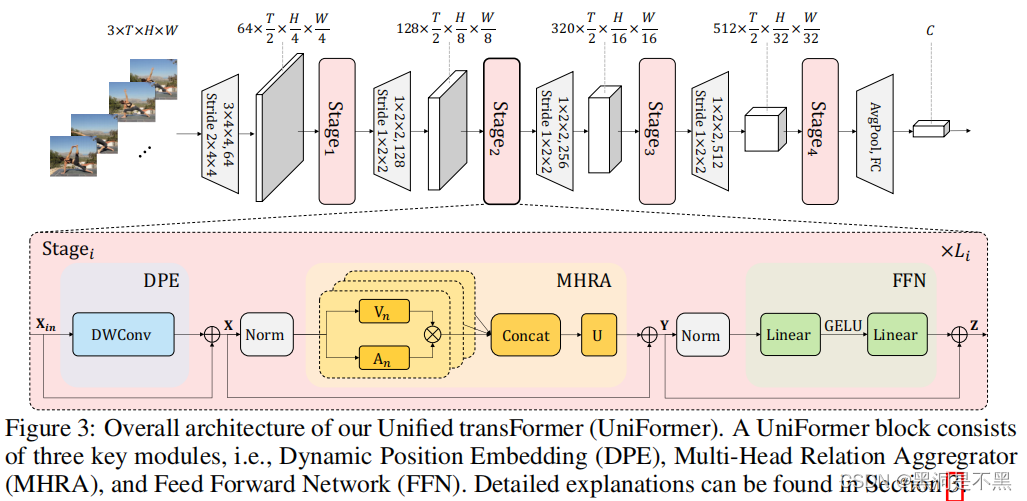
为了克服时空冗余和依赖的问题，本文提出Unified transFormer (UniFormer)框架，如图所示。每个UniFormer block主要由三部分组成：Dynamic Position Embedding (DPE), Multi-Head Relation Aggregator (MHRA) 和 Feed-Forward Network (FFN) 最核心是MHRA和DPE的设计：
X = DPE ( X i n ) + X i n Y = MHRA ( Norm ( X ) ) + X Z = FFN ( Norm ( Y ) ) + Y \begin{array}{l} \mathbf{X}=\operatorname{DPE}\left(\mathbf{X}_{i n}\right)+\mathbf{X}_{i n} \\ \mathbf{Y}=\operatorname{MHRA}(\operatorname{Norm}(\mathbf{X}))+\mathbf{X} \\ \mathbf{Z}=\operatorname{FFN}(\operatorname{Norm}(\mathbf{Y}))+\mathbf{Y} \end{array} X=DPE(Xin)+XinY=MHRA(Norm(X))+XZ=FFN(Norm(Y))+Y
2.1 MHRA：
如上所述，问题是要解决大的局部冗余和复杂的全局依赖，以实现高效和有效的时空表示学习。不幸的是，流行的3D cnn和时空Transformer只关注这两个挑战中的一个。因此，这里设计了一个Relation Aggregator (RA)，其可以将3D卷积和时空self-attention灵活地统一在一个简洁的transformer块中，分别解决了浅层和深层的视频冗余和依赖。具体地，具体来说，MHRA通过multi-head融合进行token关系学习，RA的关键是如何在视频中学习 A n A_n An ：
R n ( X ) = A n V n ( X ) MHRA ( X ) = Concat ( R 1 ( X ) ; R 2 ( X ) ; ⋯ ; R N ( X ) ) U \begin{aligned} \mathrm{R}_{n}(\mathbf{X}) &=\mathrm{A}_{n} \mathrm{~V}_{n}(\mathbf{X}) \\ \operatorname{MHRA}(\mathbf{X}) &=\operatorname{Concat}\left(\mathrm{R}_{1}(\mathbf{X}) ; \mathrm{R}_{2}(\mathbf{X}) ; \cdots ; \mathrm{R}_{N}(\mathbf{X})\right) \mathbf{U} \end{aligned} Rn(X)MHRA(X)=An Vn(X)=Concat(R1(X);R2(X);⋯;RN(X))U
- Local MHRA: （stage1和stage2中使用）在浅层中，目标是学习三维小邻域中局部时空背景下的详细视频表示。这与3D卷积滤波器的设计有着相似的见解。我们将token affinity设计为一个在局部3D邻域中操作的可学习的参数矩阵（这个与local self-attention设计很像），其值仅取决于token之间的相对3D位置。
A n local ( X i , X j ) = a n i − j , where j ∈ Ω i t × h × w , (6) \mathrm{A}_{n}^{\text {local }}\left(\mathbf{X}_{i}, \mathbf{X}_{j}\right)=a_{n}^{i-j}, \text { where } j \in \Omega_{i}^{t \times h \times w} \text {, } \tag{6} Anlocal (Xi,Xj)=ani−j, where j∈Ωit×h×w, (6)
- Global MHRA: （在stage3和stage4中使用）在深层，关注于在全局视频片段中捕获long-term token依赖关系。这自然与self-attention的设计有着相似的见解。
A n global ( X i , X j ) = e Q n ( X i ) T K n ( X j ) ∑ j ′ ∈ Ω T × H × W e Q n ( X i ) T K n ( X j ′ ) (7) \mathrm{A}_{n}^{\text {global }}\left(\mathbf{X}_{i}, \mathbf{X}_{j}\right)=\frac{e^{Q_{n}\left(\mathbf{X}_{i}\right)^{T} K_{n}\left(\mathbf{X}_{j}\right)}}{\sum_{j^{\prime} \in \Omega_{T \times H \times W}} e^{Q_{n}\left(\mathbf{X}_{i}\right)^{T} K_{n}\left(\mathbf{X}_{j^{\prime}}\right)}}\tag{7} Anglobal (Xi,Xj)=∑j′∈ΩT×H×WeQn(Xi)TKn(Xj′)eQn(Xi)TKn(Xj)(7)
2.2 DPE
扩展了conditional position encoding (CPE)设计的（DWConv是指简单的零填充的3D depth convolution）。用3D深度卷积来进行位置编码。Kernel size=333，得益于共享参数和卷积的局部性，DPE可以适用于任意长度的视频序列。 DPE ( X i n ) = DWConv ( X i n ) (8) \operatorname{DPE}\left(\mathbf{X}_{i n}\right)=\operatorname{DWConv}\left(\mathbf{X}_{i n}\right)\tag{8} DPE(Xin)=DWConv(Xin)(8)
2.3 FFN
这篇关于Uniformer: Unified Transformer for Efficient Spatial-Temporal Representation Learning的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
