本文主要是介绍【计算机图形学】3D Implicit Transporter for Temporally Consistent Keypoint Discovery,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对3D Implicit Transporter for Temporally Consistent Keypoint Discovery的简单理解
文章目录
- 1. 现有方法限制和文章改进
- 2. 方法
- 2.1 寻找时间上一致的3D特征点
- 2.1.1 3D特征Transporter
- 2.1.2 几何隐式解码器
- 2.1.3 损失函数
- 2.2 使用一致特征点的操纵
1. 现有方法限制和文章改进
用于探测特征点的、已经存在的2D和3D方法主要依赖于几何一致性来获得空间上的对齐,而忽视了时间上的一致性。
为了解决这个问题,Transporter在2D数据上,聚合时间和空间信息,进而从原始帧重建目标帧。然而2D Transporter不能直接应用于3D点云上,因为3D点云和2D图像存在结构上的差异。
因此,文章提出了第一个3D版本的Transporter,充分利用混合3D表示、跨注意力机制、隐式重建。在3D铰接物体和非刚性动物(人类和啮齿动物)上应用这种新的学习系统,从而展示了学习到的特征点在时空上的一致性。另外提出了一种closed-loop的控制策略,利用学习到的特征点来进行3D物体操纵,证明其表现。
2. 方法
文章的感知方法提出了一种新的方式,以自监督的方式,在一系列点云中发现移动物体和物体部件在时间和空间上一致的3D特征点。
一旦训练好,学习到的特征点可以被用于设计从初始状态到目标状态的铰接物体的操纵策略,从而避免了UMPNet和Where2Act策略搜集的试错。
2.1 寻找时间上一致的3D特征点
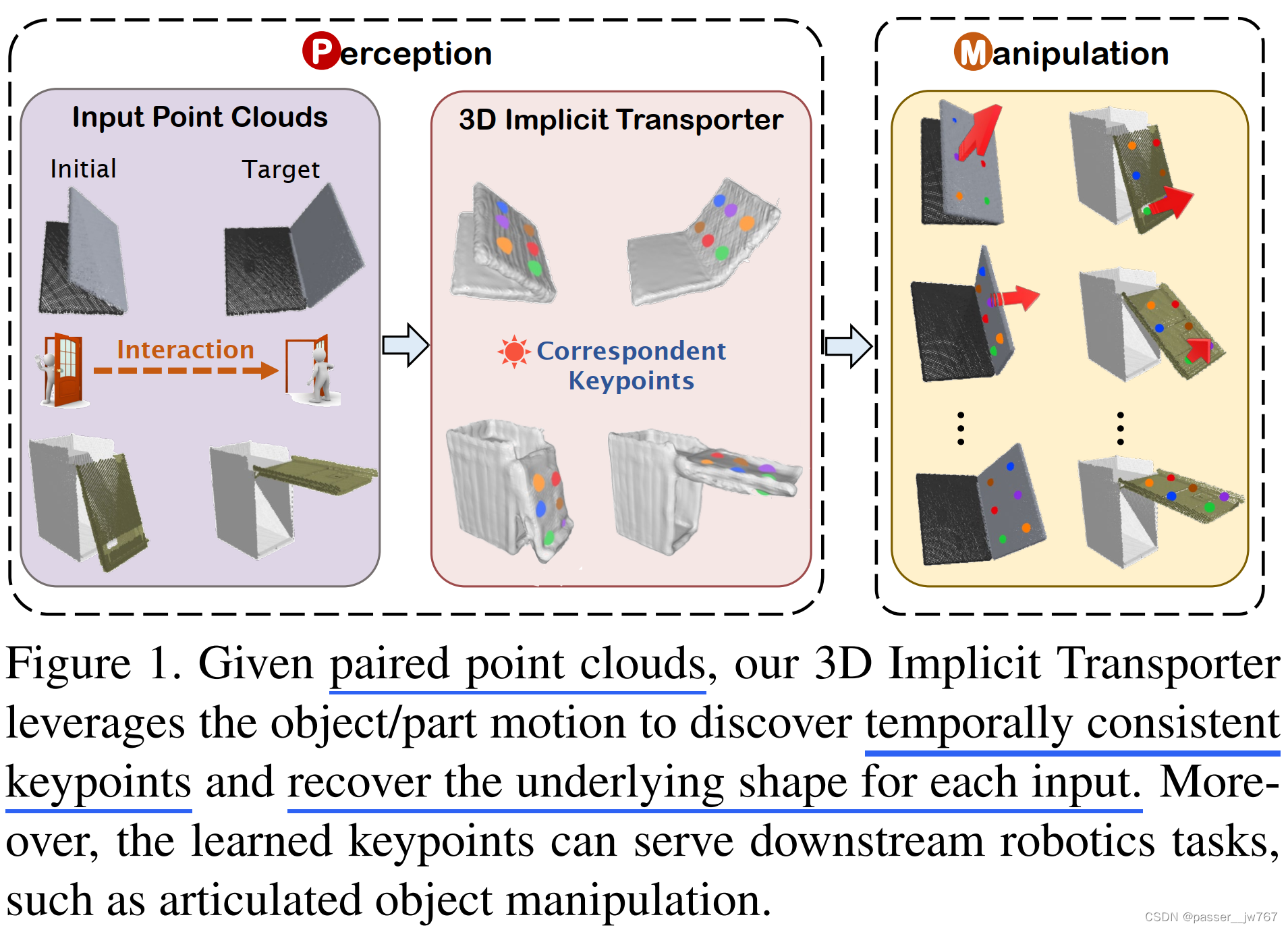
根据[23],数据集的组成是一对对的、从一系列策略中提取出来的帧,每一帧是一个3D点云。一对点云之间是通过物体的姿态/几何(有点类似于Template的概念吗?同一类别下的物体可以泛化?)来辨别差异的。文章的目标是去寻找从源帧到目标帧的、能够描述物体或物体运动部件的对应特征点。文章对这个问题的处理方式是从源帧构建目标帧的基本形状。如下图所示。
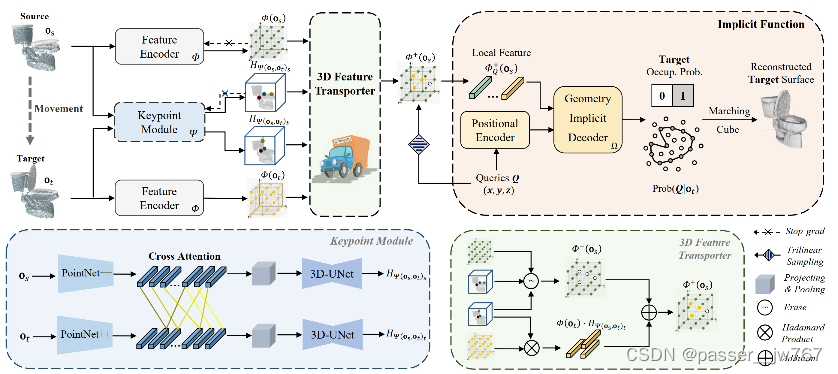
2.1.1 3D特征Transporter
混合的3D表示: 2D图像这种规则数据的对应不适用于不规则的3D点云数据。将点云统一成3D体素网格是最直接的方式,但转换成体素也会引起一些几何结构的信息丢失,比如表面可能不够精确等。尽管可以使用高分辨率的体素网格,但也会带来计算和空间上的成本。
相反,基于点的模型凭借其稀疏表示可以大大减少这些成本,因此,文章利用了基于点的backbone来从稀疏的点钟提取局部特征,利用给予体素的模型来实现局部特征迁移。
给定一帧 o ∈ R N 1 × 3 o∈\R^{N_1×3} o∈RN1×3, N 1 N_1 N1是输入点的数量,利用PointNet P P P来获得逐点特征 P ( o ) ∈ R N 1 × C 1 P(o)∈\R^{N_1×C_1} P(o)∈RN1×C1, C 1 C_1 C1是特征维度数。这些特征局部池化并投影到结构化网格 v ∈ R C 2 × C h × C w × C d v∈\R^{C_2×C_h×C_w×C_d} v∈RC2×Ch×Cw×Cd中。使用3D-UNet U U U来处理特征体素得到输出 U ( v ) ∈ R C 3 × C h × C w × C d U(v)∈\R^{C_3×C_h×C_w×C_d} U(v)∈RC3×Ch×Cw×Cd。这些步骤通过图2的特征编码器 Φ Φ Φ实现。
注意力特征点探测: 当被要求在一对帧之间寻找移动物体或移动部件时,采用迭代检查和筛选的方式来在帧之间寻找多个试探性区域。受启发于之前的工作,提出使用跨注意力机制模块来聚集两帧的几何信息来定位特征点。
利用基于点的模型来提取输入点云多层特征,进而实现两帧点云之间的关联。给定一对帧 o s , o t o_s,o_t os,ot,利用共享的PointNet++ P ^ \hat{P} P^来获得两个下采样的点特征 f s = P ^ ( o s ) f_s=\hat{P}(o_s) fs=P^(os)和 f t = P ^ ( o t ) f_t=\hat{P}(o_t) ft=P^(ot),且 f s , f t ∈ R N 2 × C 4 f_s,f_t∈\R^{N_2×C_4} fs,ft∈RN2×C4。接着使用跨注意力机制来混合这对输入之间的点特征:
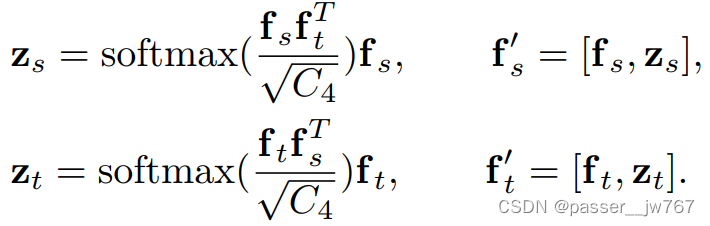
模块的输出( f s ′ , f t ′ f'_s,f'_t fs′,ft′)是输入特征和注意力特征的concatenation。接着通过PointNet++解码器上采样 f s ′ , f t ′ f'_s,f'_t fs′,ft′以获得dense features f s ′ , f t ′ ∈ R N 1 × C 5 f'_s,f'_t∈\R^{N_1×C_5} fs′,ft′∈RN1×C5。
通过以上操作,通过投影和3D UNet U k U_k Uk 将dense point features转换为keypoint saliency volumes(不知道怎么翻译)。整个检测模块的输出表示为 Ψ Ψ Ψ,分别为 Ψ ( o s , o t ) s , Ψ ( o s , o t ) t ∈ R m × C h × C w × C d Ψ(o_s,o_t)_s,Ψ(o_s,o_t)_t∈\R^{m×C_h×C_w×C_d} Ψ(os,ot)s,Ψ(os,ot)t∈Rm×Ch×Cw×Cd,从中可以提取出 m m m个3D关键点 k s , k t ∈ R m × 3 k_s,k_t∈\R^{m×3} ks,kt∈Rm×3,如图2的蓝色部分所示。 k s 和 k t k_s和k_t ks和kt的第 i i i个特征点彼此对应。
Feature Transportation: 类似于2D Transporter,下一步就是feature transportation以从 o s o_s os中重建 o t o_t ot。Transport Φ ( o t ) Φ(o_t) Φ(ot)的 k t k_t kt周围的特征至 Φ ( o s ) Φ(o_s) Φ(os)中,压缩 Φ ( o s ) Φ(o_s) Φ(os)中 k t , k s k_t,k_s kt,ks的特征。如图2绿色部分所示。首先擦除 Φ ( o s ) Φ(o_s) Φ(os)中两个集的特征得到 Φ − ( o s ) Φ^-(o_s) Φ−(os),接着从 o t o_t ot中提取特征点 k t k_t kt周围的特征,最后连接到 Φ ( o s ) Φ(o_s) Φ(os)中生成 Φ + ( o s ) Φ^+(o_s) Φ+(os),公式化为:
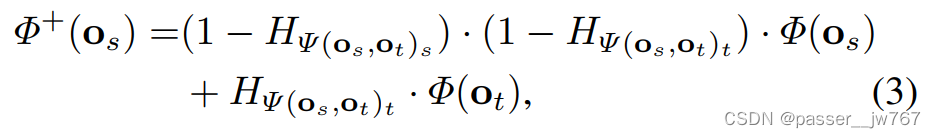
其中 H Ψ H_Ψ HΨ表示由固定方差 σ \sigma σ各向同性高斯线组成的3D热力图,以 Ψ Ψ Ψ表示的 m m m个关键点为中心。
2.1.2 几何隐式解码器
由于源和目标帧之间除运动部件外的几何形状保持相同,使用探测到的移动部件上的特征点可以重新合成目标视觉输入。受到3D重建中深度隐式函数的启发,这里使用几何隐式解码器。
给定查询集 Q Q Q中的点 q ∈ R 3 q∈\R^3 q∈R3,文章的方法使用MLP将点编码成 C e C_e Ce维的向量 q e q_e qe。接着,通过三线性插值从 Φ + ( o s ) Φ^+(o_s) Φ+(os)查询 Φ q + ( o s ) Φ^+_q(o_s) Φq+(os)。隐式解码器 Ω Ω Ω将特征 q e q_e qe和 Φ q + ( o s ) Φ^+_q(o_s) Φq+(os)连接后的结果map到目标表面占用率: Ω ( q e , Φ q + ( o s ) ) → P r o b ( q ∣ o t ) Ω(q_e,Φ^+_q(o_s))→Prob(q|o_t) Ω(qe,Φq+(os))→Prob(q∣ot)。
2.1.3 损失函数
所有模块都可以通过表面重建损失来优化。在预测的目标表面占用率 P r o b ( q ∣ o t ) Prob(q|o_t) Prob(q∣ot)和目标帧的GT标签 P r o b g t ( q ∣ o t ) Prob^{gt}(q|o_t) Probgt(q∣ot)中使用二分类交叉熵损失。如果 q q q来自目标点云,则 P r o b ( q ∣ o t ) Prob(q|o_t) Prob(q∣ot)为1,反之为0,损失函数为:

除此之外,还使用了额外的损失项 L o c c s L_{occ_s} Loccs,通过利用其自身的特征网格 Φ ( o s ) Φ(o_s) Φ(os)来辅助源帧的重建。
2.2 使用一致特征点的操纵
使用特征点作为中层表示,对于接触丰富的机器人3D空间操纵任务来说是一种合适的方式。之前的工作仅关注与2D特征点表示,或在面对巨大的shape变化或物体拓扑改变的情况下,难以探测到时空一致的3D特征点。由于3D Transporter特征点的长期一致性,文章的方法很好地处理了3D操纵任务。此处以铰接物体操纵作为基线来证明。
在UMPNet工作中,给定目标状态 o g o_g og,目标是生成机器人的end-effector从当前状态 o c o_c oc转变到目标状态 o g o_g og的一组动作。在本片工作中,每个状态使用点云而不是2D图像表示,使用吸盘手以实现对物体表面任意一个点的抓取。
特征点一致性损失: 由于预测的特征点分布在预测的移动部件上,可以使用它来生成源和目标之间的刚性部件运动姿态假设:
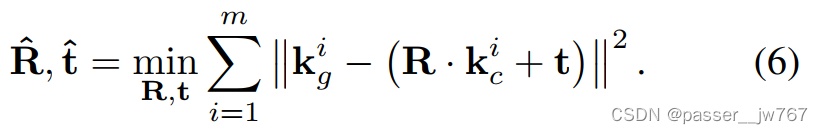
可以使用奇异值分解在封闭形式下计算。强制所有特征点满足刚性转换,使关键点几何对齐:
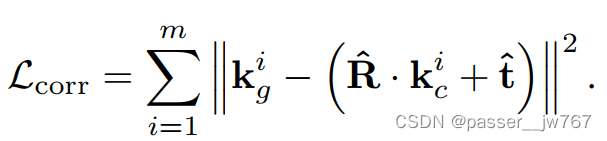
关节一致性损失: 铰接运动过程中,轴的方向要么保持不变要么平行。给定预测的姿态,可以通过Rodrigues旋转公式计算轴的方向 μ μ μ和角度 θ \theta θ,惩罚不同时间步下的轴的方向:
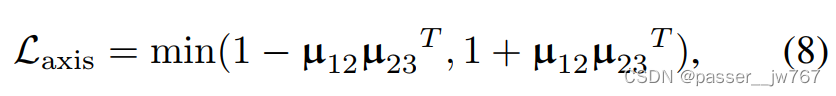
其中, μ a b μ_{ab} μab表示在时间步 a a a和时间步 b b b中预测的轴方向。
完整的损失就是occupancy loss加上这个corr和axis。
在训练后设计了一个基于3D Implicit Transporter keypoint的对象无关的操纵策略,避免了低效探索。对于每个将物体从current state移动到goal state的动作 A c , g A_{c,g} Ac,g,6-Dof姿态表示吸盘手的位置 A c , g p o s ∈ R 3 A^{pos}_{c,g}∈\R^3 Ac,gpos∈R3和移动方向 A c , g d i r ∈ R 3 A^{dir}_{c,g}∈\R^3 Ac,gdir∈R3,策略由两个部分组成:
位置和方向推理: 第一步是获得预测特征点 k c , k g k_c,k_g kc,kg,轴 μ c , g μ_{c,g} μc,g,角度 θ c , g \theta_{c,g} θc,g。接着从对应特征点计算系数铰接流 F c , g i = k g i − k c i F^i_{c,g}=k^i_g-k^i_c Fc,gi=kgi−kci。为有效驱动铰接部件,根据杠杆原理选择具有最高magnitude flow的关键点位置 k c s k^s_c kcs作为吸力点,表示为 A c , g p o s = k c s A^{pos}_{c,g}=k^s_c Ac,gpos=kcs。
对于旋转轴, k c s k_c^s kcs被限制在垂直于旋转轴的半径为 r s r^s rs的2D圆上,其中 r s r^s rs是从 k c s k^s_c kcs到关节的最短向量。因此, k c s k_c^s kcs的理想行动方向与 A c , g d i r s A^{dir_s}_{c,g} Ac,gdirs相切。若当前状态和目标状态的运动范围较小,则 F c , g s F^s_{c,g} Fc,gs将近似平行于 A c , g d i r s A^{dir_s}_{c,g} Ac,gdirs,则可被设置为运动方向。然而随着旋转范围的增加,它们之间的差异也会越来越显著,减轻这个问题的方法就是根据预测的轴多插值几个中间状态。
对于平移轴, A c , g d i r s A^{dir_s}_{c,g} Ac,gdirs平行于每个移动点的GT铰接流的。直接设置 F c , g s F^s_{c,g} Fc,gs作为铰接方向。不需要区分关节类型,两种方法在极小的差异内都是一样的。
闭环操纵: 与使用单个步骤动作实现目标不同,该工作生成一系列动作来逐渐改变铰接状态。应用一个closed-loop的控制系统,依赖于反馈来逐渐调整当前动作。特别地,基于物体当前状态和目标状态来预测下一个动作。不同于UMPNet使用一个常数移动距离,这里利用 F c , g s F^s_{c,g} Fc,gs的大小来动态调整移动距离。受到PID控制器的启发,设置 ∣ ∣ A c , g d i r s ∣ ∣ = λ ⋅ ∣ ∣ F c , g s ∣ ∣ ||A^{dir_s}_{c,g}||=\lambda·||F^s_{c,g}|| ∣∣Ac,gdirs∣∣=λ⋅∣∣Fc,gs∣∣作为当前状态, λ \lambda λ是一个比例系数。
这篇关于【计算机图形学】3D Implicit Transporter for Temporally Consistent Keypoint Discovery的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








