本文主要是介绍【深蓝学院】移动机器人运动规划--第5章 最优轨迹生成--笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1. Preliminaries
- 2. Multicopter dynamics and differential flatness(多旋翼动力学和微分平坦特性)
- 2.1 Differential Flatness
- 2.2 具体建模
- 2.3 Flatness Transformation的解析推导
- 3. Trajectory Optimization轨迹优化
- 3.1 Problem formulation
- 3.2 Unconstrained case
- 3.3 Unconstrained Case: BIVP(Multi-segment with intermediate values)
- 3.4 Constrained Case
- 3.4.1 Constrained Case: Convex Simplification
- 3.4.2 Issues of simplification
- 3.4.3 Constrained Case: Spatial-Temporal Deformation (Brief)
- 4. Reference
1. Preliminaries

Ch2讲了基于搜索的路径规划方法,Ch3讲了基于采样的路径规划方法,这些都是global methods,框架都是Exploration and Exploitation,且在算力足够大的情况下,一定能够找到全局最优解。
除了global methods,还有local methods,主要是Deterministic Optimization确定性优化。基于优化的方法,主要是利用cost function的0阶和高阶导数来进行优化(如梯度下降,迅速地寻找到一个局部极小值local minimum),与global methods不同的是,此类方法少了探索的过程,所以不能保证结果最优。
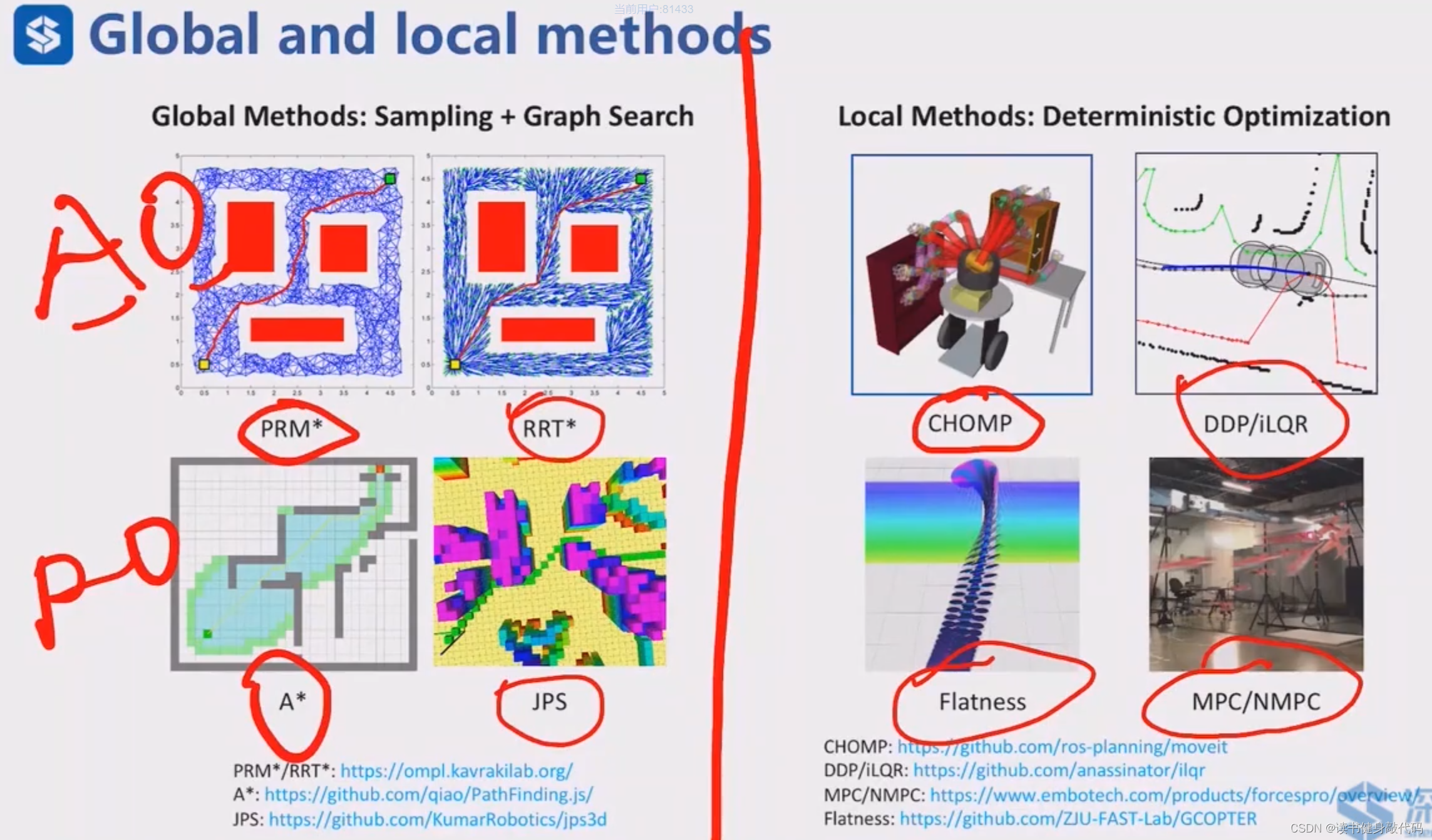
PRM*,RRT* 是AO(Asymptotic Optimality)渐进最优的方法,A*,JPS是RO(Resolution Optimality)分辨率最优的方法。这些均属于global methods,在低维时(如4维一以下)工作较好,但高维时就需要实时性更好的方法。
右侧的均为local methods,CHOMP用于多机械臂轨迹优化,DDP/iLQR用于无人车规划,Flatness用于无人机,MPC/NMPC用于一般的机器人轨迹优化,这类方法一般实时性较高。

如上为global methods和local methods的优缺点对比。

global和local methods在实现上经常被分为前端和后端,可以把来自环境的复杂度和来自于动力学约束的复杂度分而治之[1,2,3,4]。
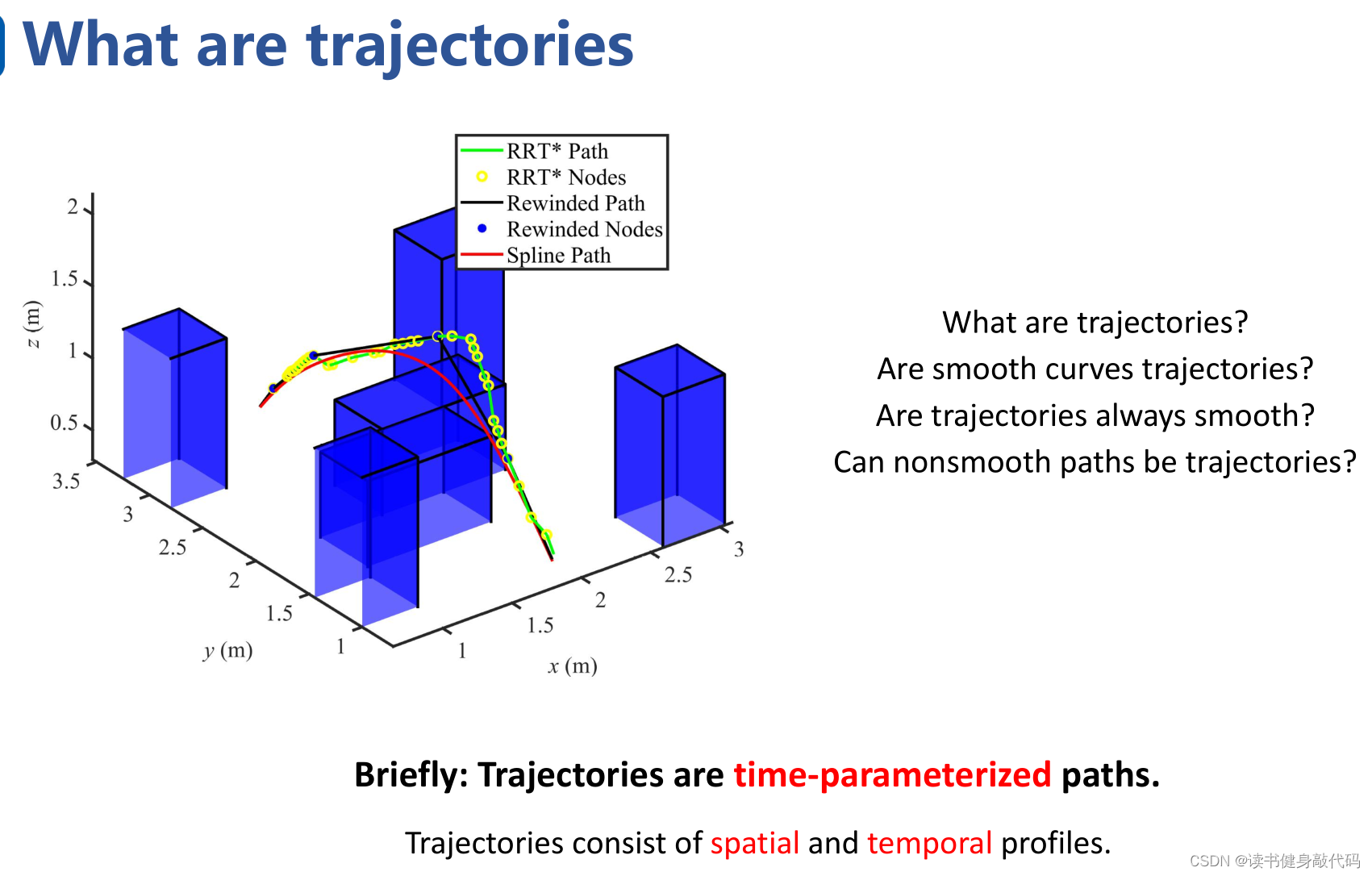
Q1:什么是轨迹?
A1:Trajectories are time-parameterized paths.
轨迹是时间参数化的路径。
Q2:Are smooth curves trajectories?
A2:smooth curves不是traj,因为没有时域信息,没有时域信息的均当作curves处理。
Q3:Are trajectories always smooth?
A3:几何学与动力学的smoothness不同,所以traj不一定smooth。
Q4:Can nonsmooth paths be trajectories?
A4:几何上非光滑的path也可以是traj。
trajectory是同时包含时间和空间特性的。
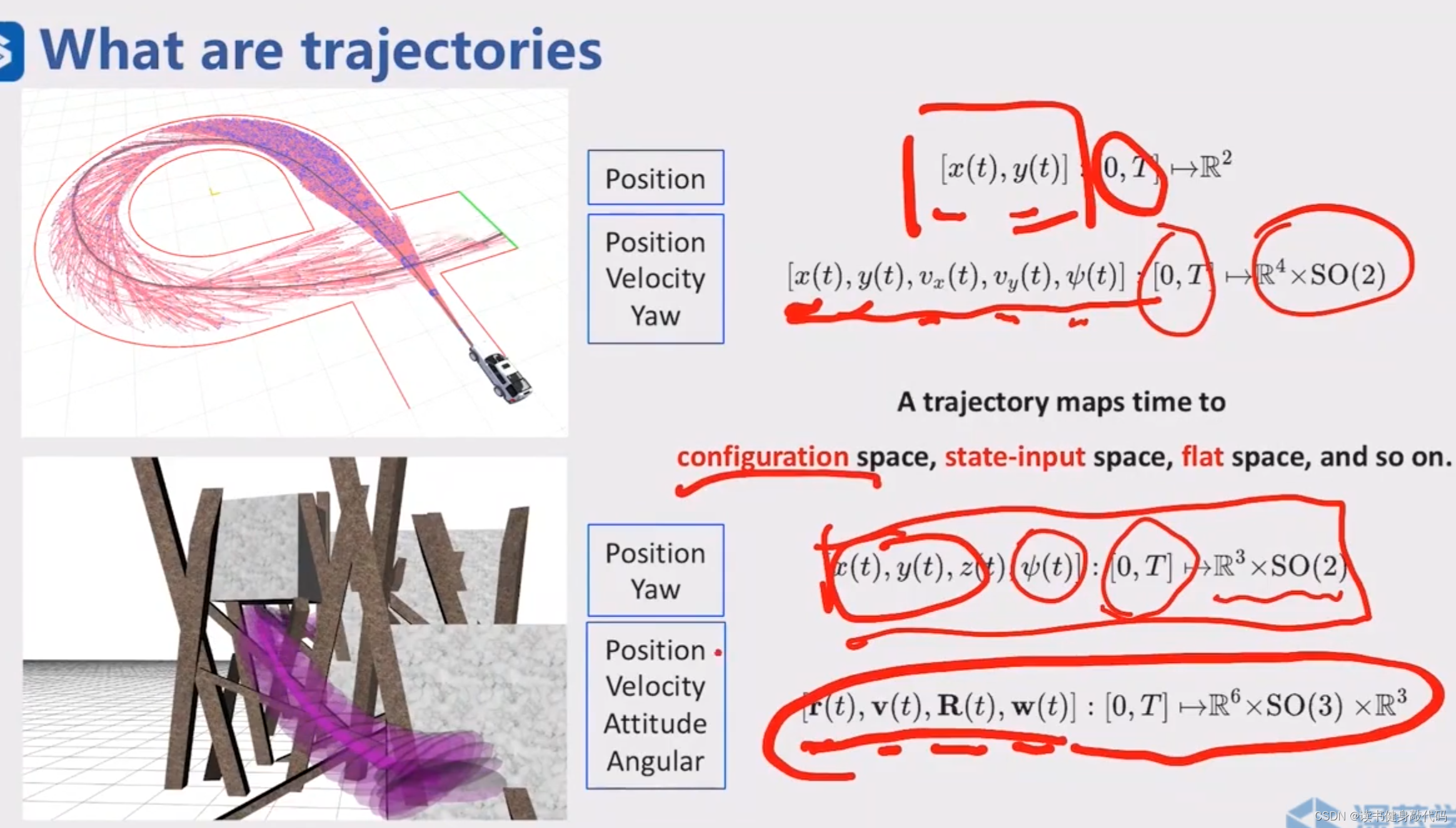
traj就是把时间映射到各种space中,space中可能包含位置,速度,偏航角,旋转等。
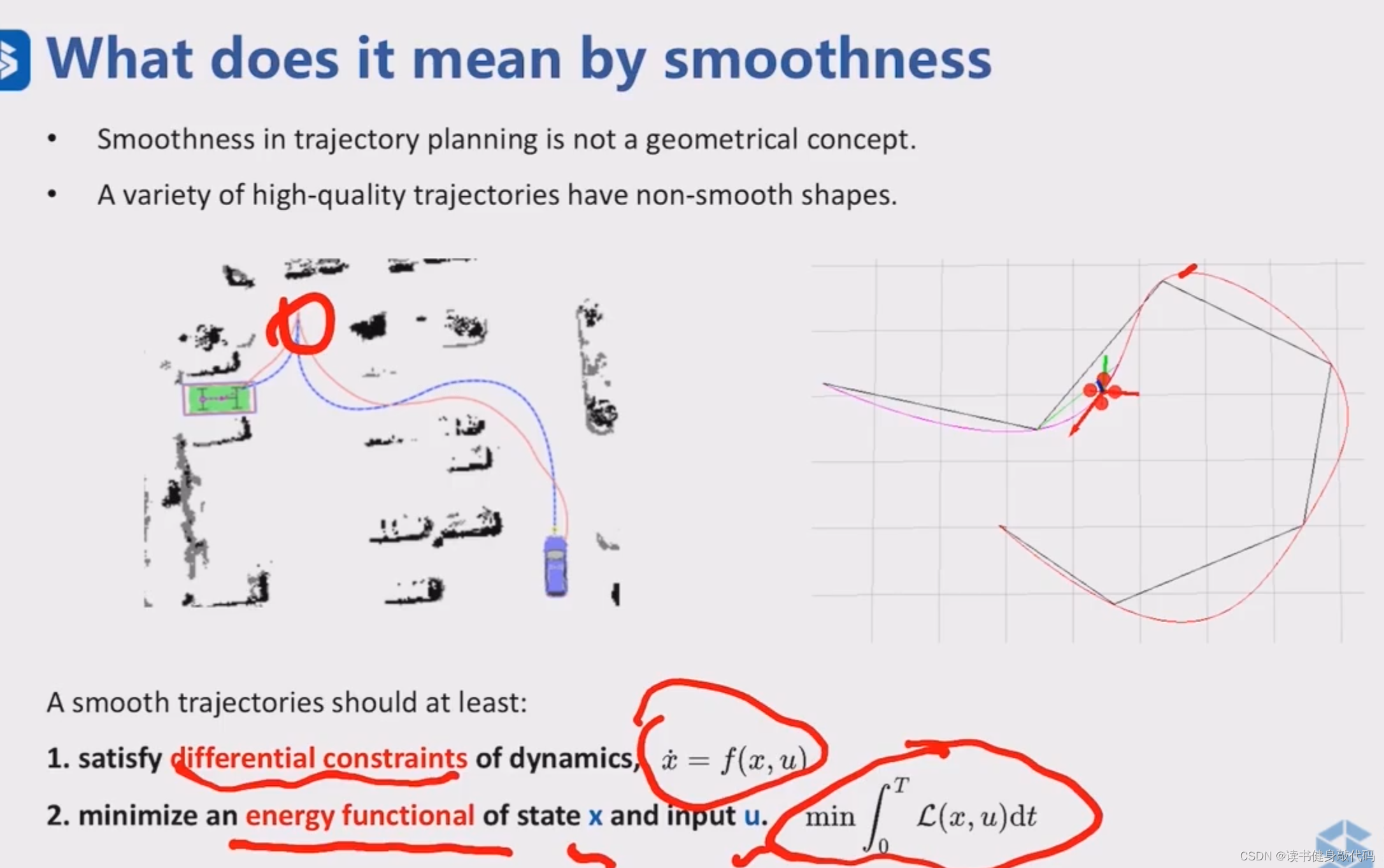
一个smooth的traj至少要
- 满足微分约束(系统方程通常由常微分方程给出),
- 最小化能量泛函(最小化cost,如能量消耗等)
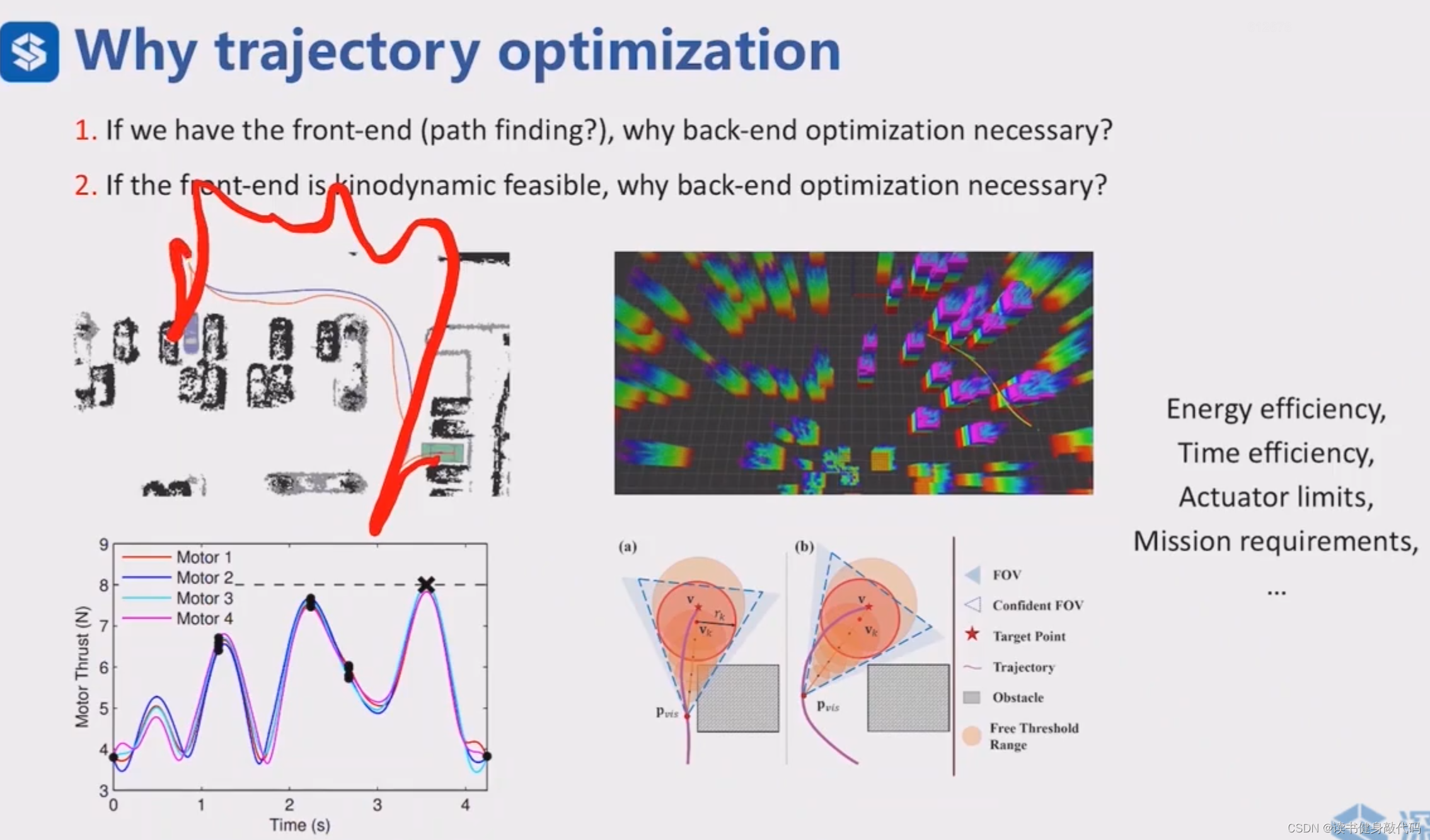
为什么后端是必须的?
尽管有一些考虑了kinodynamaic的前端生成一些path,给出一些traj的初值,但是后端可以进一步优化,在前端结果不那么好的时候也能收敛到较好的结果。
除了考虑动力学约束,还需要考虑很多其他约束,如时间效率,驱动器限制,任务要求等,综合考虑这么多约束,优化是一种非常好的方法。
2. Multicopter dynamics and differential flatness(多旋翼动力学和微分平坦特性)
2.1 Differential Flatness

简单来说,对于由常微分方程(ODE,Ordinary Differential Equation)描述的系统,在对系统施加了各种约束之后,由系统状态 x x x,系统状态的导数 x ˙ \dot{x} x˙,输入 u u u所张开的空间 R R R中,满足约束的解 z z z 只能在该空间的一个曲面上移动,为了进行求解,引入了微分平坦变换(differential flatness transformation),能够在一个无约束的空间中对轨迹 z z z 进行优化,这个优化结果也是满足 R R R中的约束的,微分平坦变换就是上图的 Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu,该变换消除了微分约束,降低优化难度,在优化出 z z z之后,可以通过微分平坦变换求出 x , u x,u x,u,是满足微分约束的。
(该部分比较数学,细节如果需要的话再深入探讨)

桨对齐的四旋翼/多旋翼,线性风阻的多旋翼,桨以一定规律排布的多旋翼都满足differential flatness[5,6,7,8,9].

虽然使用differential flattness能够简化无人机的优化问题,但是有两个问题需要考虑:
- 无人机实际飞行时需要考虑风阻drag(因为速度快时必须考虑风阻)
- differential flattness存在奇异点,需要尽可能降低奇异点个数。
上图列出了6种使用differential flattness时会出现奇异点的地方(即出现 1 0 \frac{1}{0} 01的情况)
需要说明,yaw在无人机领域不一定是传统意义上的定义,可根据应用场景定义。
1,2使用不同转序的Euler角,不考虑风阻。
3将body x轴投影至world系,与world系的x轴所成夹角即为yaw,显然奇异点在body的x轴投影与world系x轴平行时出现。
4考虑了线性的风阻。
5通过Hopf fibration定义yaw,旋转通过yaw和tilt定义(tilt即body的z轴与world的z轴所成夹角),此方法仅有一个奇异点,出现在body的z轴与重力方向平行时(即机身完全翻转时)。
6对5中的奇异点在数学上进行了证明[10]。
补充:
Hopf fibration(霍普夫纤维化)是一种在纯数学中的概念,它描述了一个四维球面如何映射到三维空间上的球面。具体而言,Hopf fibration是一个从四维单位球面(称为四维球面S3)到三维球面(称为三维球面S2)的映射。
这个映射的特殊之处在于,它将四维球面的每一个点映射到三维空间中的一个点,并且保持了一种特殊的关系:在四维球面上,每一条经线(类似于经度线)都被映射为三维球面上的一个圆,而纬线(类似于纬度线)则被映射为三维球面上的一条线。
Hopf fibration在数学和物理学中都具有重要的应用。它在拓扑学、几何学和量子场论等领域中有着广泛的研究和应用价值。这个概念的提出者是德国数学家Heinz Hopf,他在1931年首次引入了这个概念并进行了深入研究。
2.2 具体建模

参考
- state is x = r , v , R , w x={r,v,R,w} x=r,v,R,w,分别为位移,速度,旋转,在body系下的角速度,分别为
R 3 × R 3 × S O ( 3 ) × R 3 \mathbb{R}^3\times\mathbb{R}^3\times SO(3)\times \mathbb{R}^3 R3×R3×SO(3)×R3 - 输入 u u u为推力thrust的标量和3轴扭矩向量 τ \tau τ
- 动力学方程(ODE): x ˙ = f x + g ( x ) u \dot{x}=f{x}+g(x)u x˙=fx+g(x)u,后面细讲
- 平坦输出flat output: z = r , ψ z={r,\psi} z=r,ψ分别为位移 ∈ R 3 \in \mathbb{R}^3 ∈R3和2D yaw ∈ S O ( 2 ) \in SO(2) ∈SO(2)
针对无人机动力学方程:
这里的物理量均定义在world系(即惯性系)下。
- r ˙ = v \dot{r}=v r˙=v
位置对时间求导是速度。 - 牛顿第二定律 m a = F ma=F ma=F
右侧为无人机在飞行过程中收到的和力。
-
− m g e 3 -mge_3 −mge3:m质量,g重力标量, e = ( 0 , 0 , 1 ) T e=(0,0,1)^T e=(0,0,1)T表示竖直向上,与重力方向反向。该项表示无人机收到的重力(是向量)。
-
R f e 3 Rfe_3 Rfe3: R = R w b R=R_{wb} R=Rwb由body到world的旋转, f f f为总推力thrust大小。该项表示系统的推力向量在world系下的向量。
-
− R D R T σ ( ∣ ∣ v ∣ ∣ ) v -RDR^T\sigma (||\bm{v}||)v −RDRTσ(∣∣v∣∣)v:表示无人机在飞行过程中收到的风阻。
该项可如下理解:

- − R T v -R^Tv −RTv是无人机world系下速度转到body下的速度取反
- D σ ( ∣ ∣ v ∣ ∣ ) D\sigma (||v||) Dσ(∣∣v∣∣)中: ∣ ∣ v ∣ ∣ ||v|| ∣∣v∣∣表示world系下无人机速度大小,标量 σ \sigma σ表示缩放系数, D D D为对角矩阵,是风阻系数(与无人机外形等有关)。
- 故 D σ ( ∣ ∣ v ∣ ∣ ) ( − R T v ) D\sigma (||v||)(-R^Tv) Dσ(∣∣v∣∣)(−RTv)为body系下收到的风阻力向量,左乘 R R R转至world系下为 R D σ ( ∣ ∣ v ∣ ∣ ) ( − R T v ) RD\sigma (||v||)(-R^Tv) RDσ(∣∣v∣∣)(−RTv),整理为 − R D R T σ ( ∣ ∣ v ∣ ∣ ) v -RDR^T\sigma (||\bm{v}||)v −RDRTσ(∣∣v∣∣)v整体表示无人机飞行时在world系下所受的风阻力向量。
-
R ^ = R ω ^ \hat{R}=R\hat{\omega} R^=Rω^:旋转矩阵更新(反对称使用 w ^ \hat{w} w^表示,搞slam的很熟悉了)
-
M ω ˙ = τ − ω × M ω − A ( ω ) − B ( R T v ) M\dot{\omega}=\tau-\omega\times M \omega-A(\omega)-B(R^T v) Mω˙=τ−ω×Mω−A(ω)−B(RTv):欧拉公式加上修正项。其中 M ω ˙ = τ − ω × M ω M\dot{\omega}=\tau-\omega\times M \omega Mω˙=τ−ω×Mω为常见的欧拉公式, M M M为惯性张量矩阵, τ \tau τ为三轴力矩。 A ( ω ) A(\omega) A(ω):飞机转动时产生的阻尼力矩, B ( R T v ) B(R^T v) B(RTv)平动时产生的力矩。
整个系统方程中, D , σ , A , B D,\sigma,A,B D,σ,A,B可以通过参数拟合,系统辨识等方法来分别确定。
2.3 Flatness Transformation的解析推导

如果已经有了flat output,如何求出我们的目标状态呢?这时需要解析地求出微分平坦变换 Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu,需要指出, Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu的表达式很复杂,表达式也可以通过迭代的方式来给出,也即如果我们知道如何迭代地求出 x , u x,u x,u,也就相当于知道了 Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu的表达式。
下面分别给出 r , v , R , ω , f , τ r,v,R,\omega,f,\tau r,v,R,ω,f,τ的求解过程。
对系统方程中的牛顿方程两边左乘body系下的x,y轴,即 ( R e i ) T , i ∈ ( 1 , 2 ) (Re_i)^T,i\in(1,2) (Rei)T,i∈(1,2),推导出下图的结论:
v ˙ + d h m σ ( ∣ ∣ v ∣ ∣ v + g e 3 ) \begin{align} \dot{v}+\frac{d_h}{m}\sigma (||v||v+ge_3) \end{align} v˙+mdhσ(∣∣v∣∣v+ge3)
body的x,y轴与式(1)垂直

与 x b , y b x_b,y_b xb,yb垂直的只有与 z b z_b zb同向或反向,当无人机悬停时, v = 0 v=0 v=0得出式(1)为 g e 3 ge_3 ge3,为推力,与重力反向,所以式(1)与重力反向,与 z b z_b zb同向。
接着牛顿方程两边同乘 z b = ( R e 3 ) T z_b=(Re_3)^T zb=(Re3)T,可以推导出推力标量 f f f的表达式。

旋转 R R R可由偏航旋转和倾斜旋转求出,旋转与四元数是1对2的关系,即一个旋转可对应两个不同的四元数,而一个四元数可以确定一个唯一的旋转。
旋转四元数表示为旋转轴 v \bm v v和旋转角度 θ \theta θ,即 q = ( ( c o s θ ) 1 × 1 , ( v s i n θ ) 3 × 1 ) = ( w , x , y , z ) T q=((cos\theta)^{1\times1},(\bm{v}sin \theta)^{3\times1})=(w,x,y,z)^T q=((cosθ)1×1,(vsinθ)3×1)=(w,x,y,z)T
- 偏航四元数 q ψ q_\psi qψ,仅绕 e 3 = ( 0 , 0 , 1 ) T e_3=(0,0,1)^T e3=(0,0,1)T旋转,即 q ψ q_\psi qψ中 x , y = 0 x,y=0 x,y=0
- 倾斜四元数 q t i l t = q z q_{tilt}=q_z qtilt=qz不绕 z z z轴进行旋转,可视作如下的旋转:
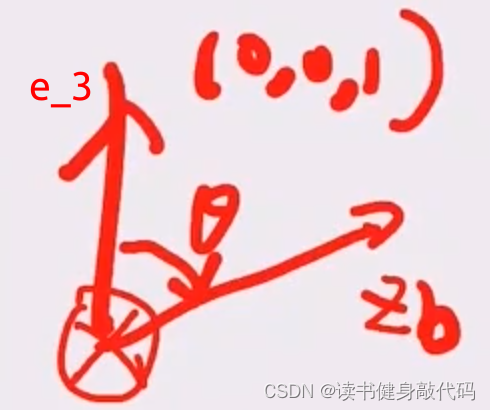
e 3 e_3 e3与目标 z b z_b zb组成平面 P P P,旋转轴为 P P P的法向量 v \bm v v,垂直向内,由 e 3 e_3 e3方向绕 v \bm v v顺时针旋转 θ \theta θ得目标 z b z_b zb,无 y a w yaw yaw方向的旋转,故 q z q_{z} qz中 z = 0 z=0 z=0
由 q ψ q_{\psi} qψ和 q z q_{z} qz可求出总体旋转四元数 q = q z ⊗ q ψ q=q_{z}\otimes q_{\psi} q=qz⊗qψ,由 q q q可唯一地确定旋转矩阵 R R R,具体操作可参考[11]。

角速度 ω \omega ω可由 R ˙ = R ω ^ \dot{R}=R\hat{\omega} R˙=Rω^求出。
同样也可求出 z b ˙ \dot{z_b} zb˙,其中 D N ( x ) \mathcal D\mathcal N(x) DN(x)表示归一化函数的一阶导数。
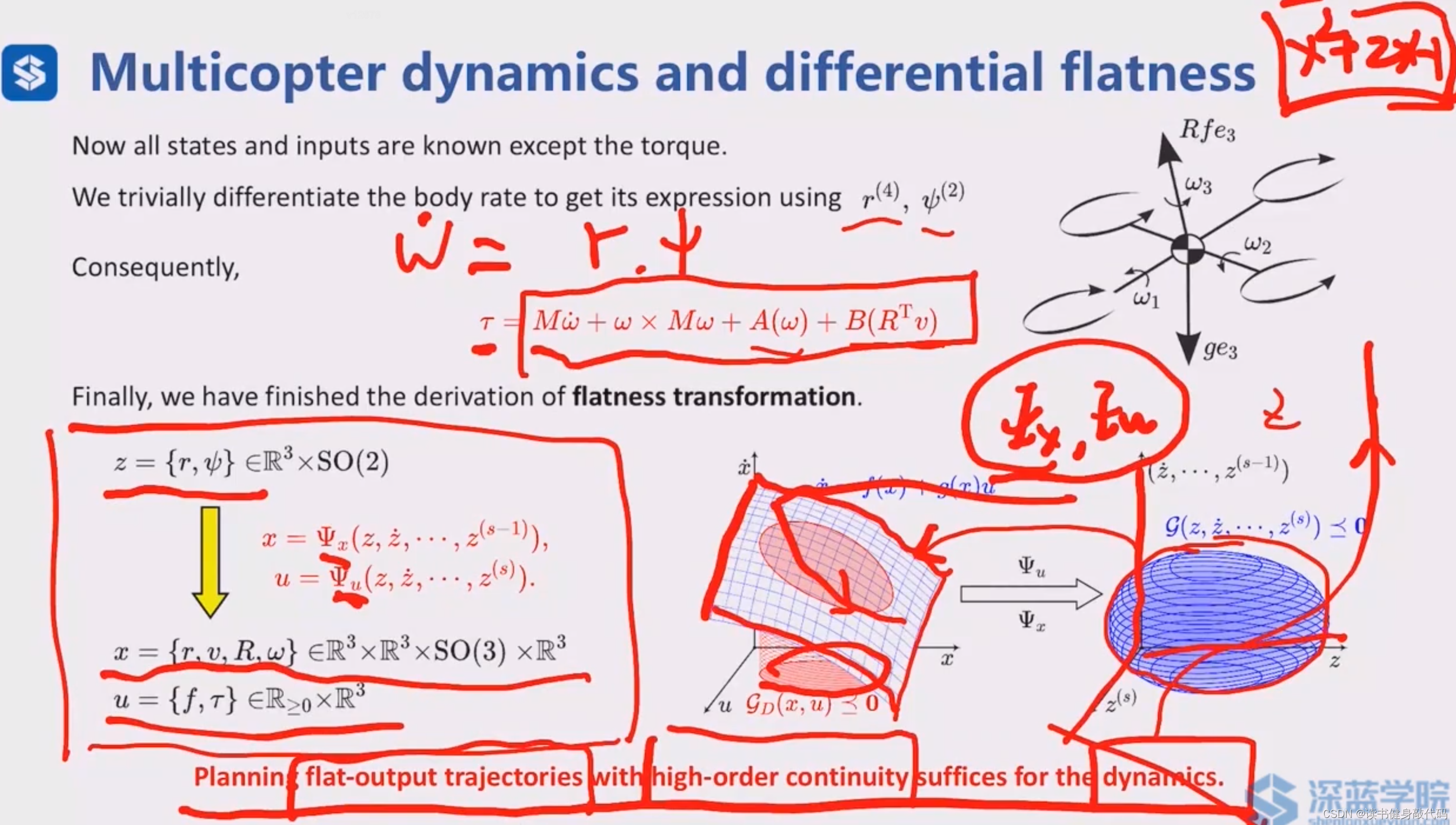
得到 ω \omega ω的公式后,根据动力学模型的欧拉公式,可以推导出torque的表达式,于是 x , u x, u x,u中的变量
r , v , R , ω , f , τ r,v,R,\omega,f,\tau r,v,R,ω,f,τ均求出,对应以上PPT中的标红部分,也即flatness transformation Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu的表达式已经求出。
利用differential flatness可以将带有等式约束的优化问题转换为没有等式约束的优化问题(但仍然存在一些不等式约束),极大提高优化求解速度。
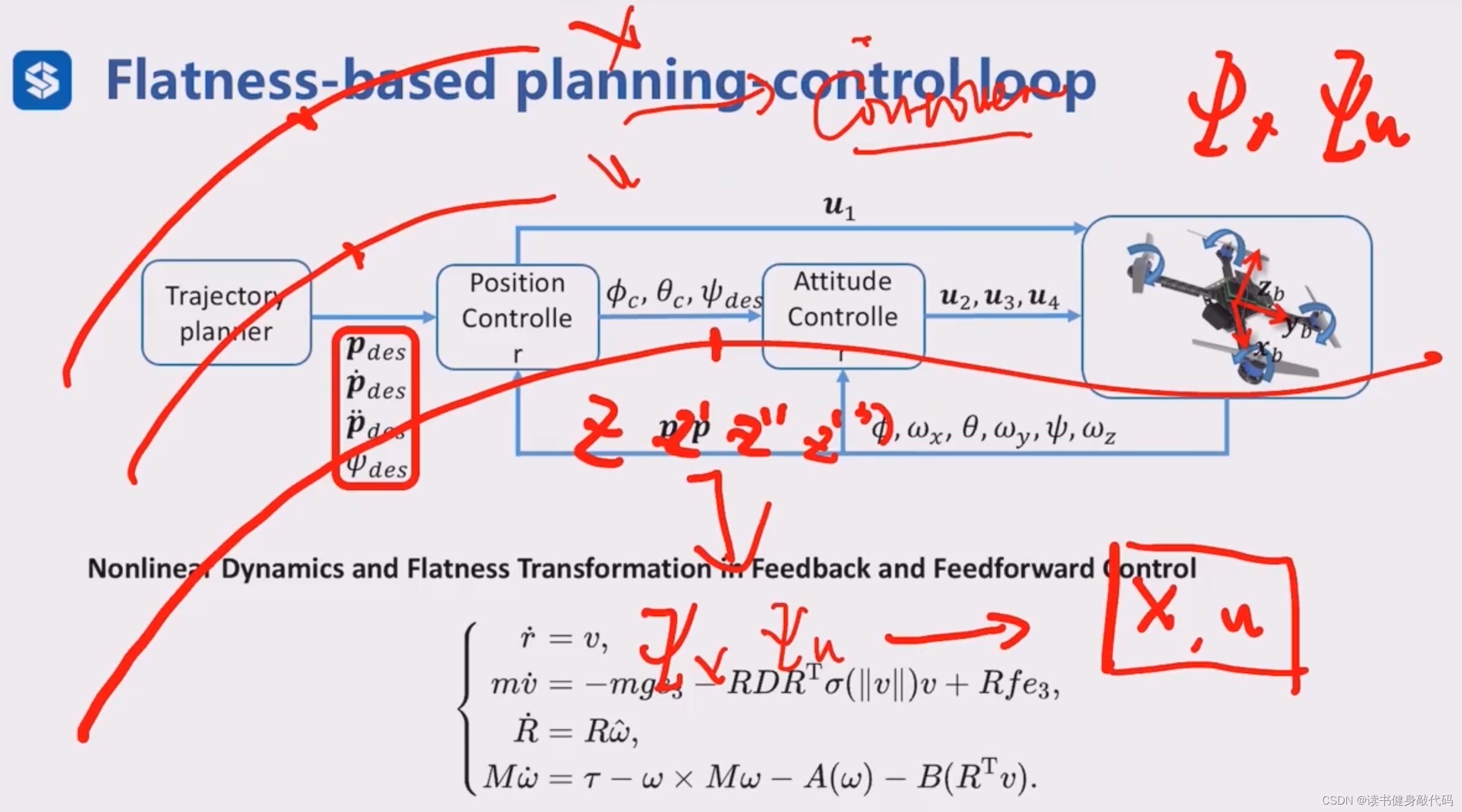
在控制方面也可以使用微分平坦特性,如反馈和前馈(cal desire,类似串级控制的内环输出)控制中的微分平坦变换。如果task为跟踪一条比较高维的轨迹 x , u x,u x,u,而我们只能控制一个四维的 z z z,可以输入高维的 x , u x,u x,u,使用flattness计算出低维的flat output,进行控制,再使用 Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu计算出高维的实际输出 x , u x,u x,u,只要输出可导即可。该过程可以看做一个压缩(flat output)和解压(flattness transformation Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu)的过程,该过程是解析地进行的,所以速度较快。

实际中,使用样条来获得flat output有以下优点:
- 容易确定是否可导;
- 容易求出闭式导数,闭式表达式等;
- 可以解耦进行,每个维度上独立进行(如x维使用2阶近似,y使用3维,z使用4维, ψ \psi ψ使用5维等);
- 计算的数值稳定性已有较多研究。
不清楚的方面:如何使用如spline这样的方法获得flat output?
3. Trajectory Optimization轨迹优化
3.1 Problem formulation

如上即为traj optimization general problem formulation.
- 我们的优化目标函数是最小化优化项的energy(加权平方积分),使其更加平滑。函数是基于平坦输出 z ( t ) z(t) z(t)而非直接的 x , u x,u x,u,具体而言,优化 z ( s ) ( t ) z^{(s)}(t) z(s)(t),s取不同值时即优化不同项,
- s=1速度,
- s=2加速度,
- s=3,jerk;
- s=4,snap
有不同的效果,后面会讲。
优化 z ( t ) z(t) z(t)的高阶导数的能量,使其更加平滑。
不光优化 z ( t ) z(t) z(t),还优化时间 T T T,如果不优化时间,当 T → + ∞ T \to +\infty T→+∞时,energy可能趋近于0,所以需要加上一个正则项 ρ ( t ) \rho (t) ρ(t)(如 ρ ( t ) = 100 T \rho (t)=100T ρ(t)=100T),使得整体的优化时间不至于过长。
-
其中 G ( z ( t ) ⋯ z ( s ) ( t ) ) < 0 \mathcal{G(z(t)\cdots z^{(s)}(t))}<0 G(z(t)⋯z(s)(t))<0是约束,不是基于 x , u x,u x,u,而是基于flat output和flatness transformation Ψ x , Ψ u \Psi_x,\Psi_u Ψx,Ψu的约束表示。和前面提到的一样,约束中的变量比较灵活,可以添加任何想要加入的变量(如控制时间,无人机倾角限制等)
-
z ( t ) z(t) z(t)需要在free space F \mathcal{F} F中,是collision-free的:由于一张地图中start->goal的拓扑组合非常多,所以给出 F \mathcal{F} F非常困难。
-
具体问题中会给出起始和末端的状态约束。
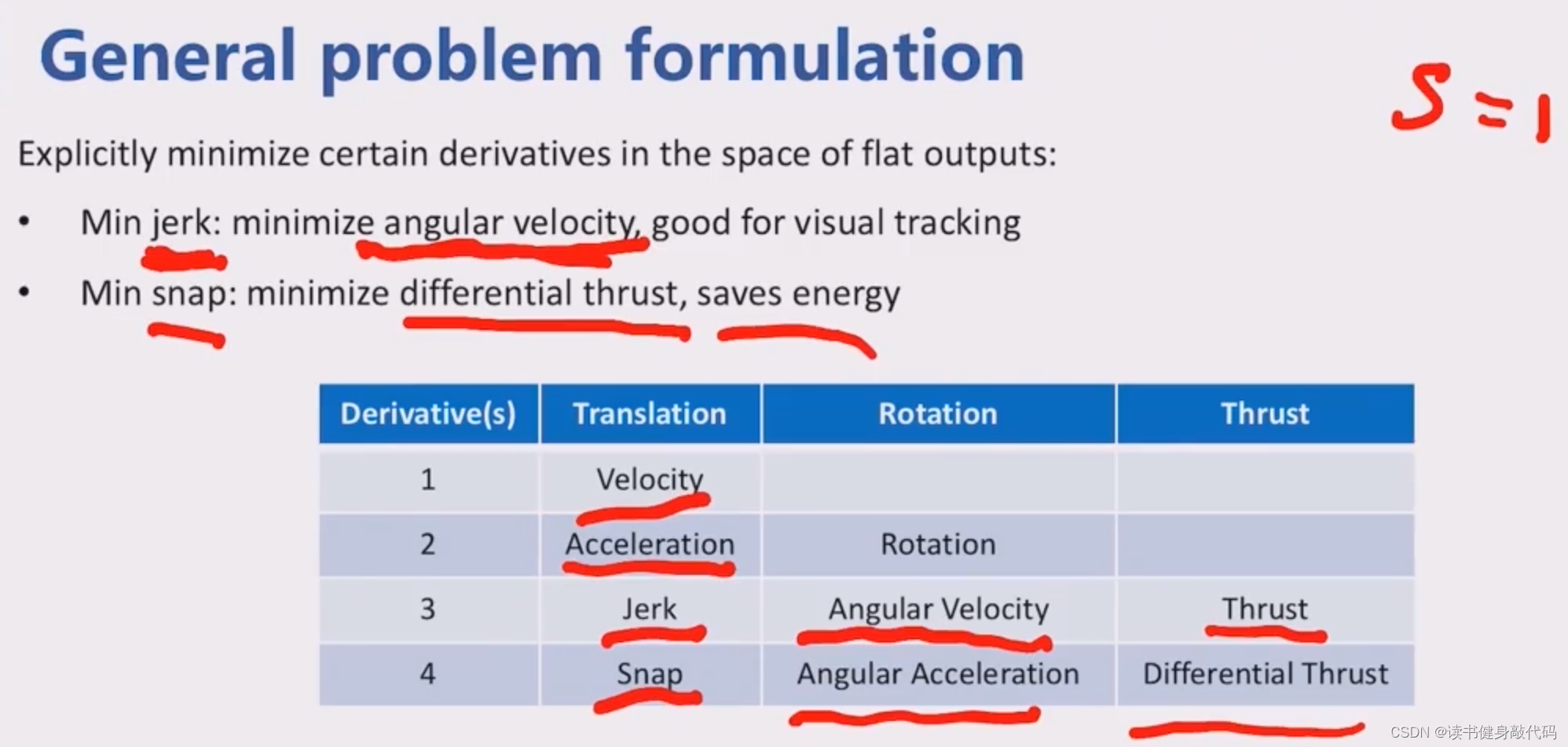
优化不同的量会有不同的效果:
- 如优化jerk的energy可以最小化角速度,便于保持稳定;优化
- 优化snap的energy可以最小化微分推力,节省能量。
3.2 Unconstrained case
学界中已经探讨出了最优性充要条件,如 F , G \mathcal{F,G} F,G约束不存在, ρ ( T ) \rho({T}) ρ(T)中 T T T已给定,约束也不存在。
下面讲解一种Unconstrained case[12],这也是本节课讲师已经发表的工作:
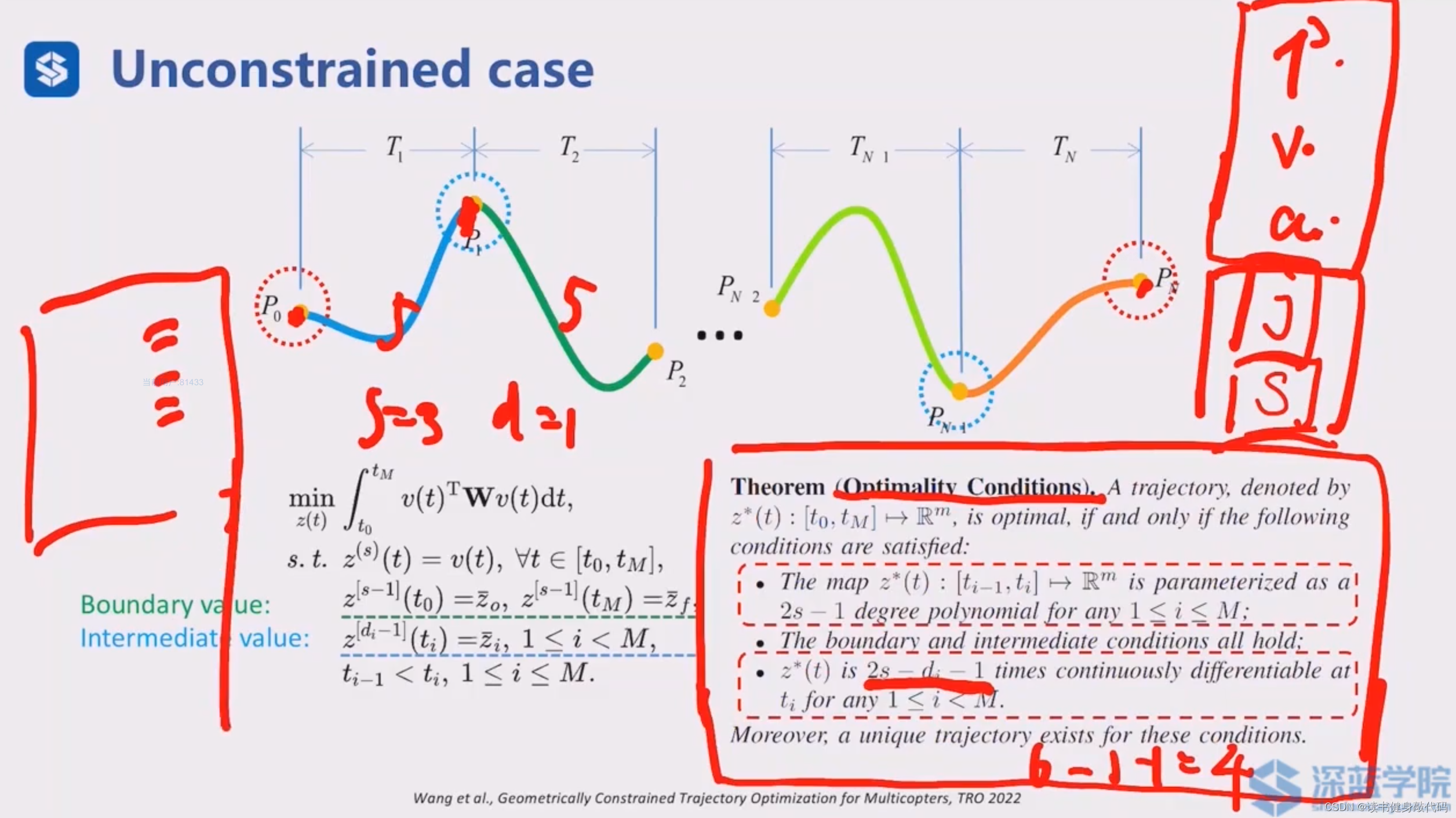
上图为最优性的条件,约束中没有 F , G \mathcal{F,G} F,G的约束,
- s=3时,最优 z ∗ ( t ) z^*(t) z∗(t)为2s-1=5次多项式
- 需满足边界和中间约束(3.3节会讲解没有中间约束,自己生成,而非给定的情况BIVP)
- d=1时, z ∗ ( t ) z^{*}(t) z∗(t)为2s-d-1=4阶连续,即其0,1,2,3,4阶导数均存在。
将各阶导数组成的等式约束联立求解即可求出最优解。
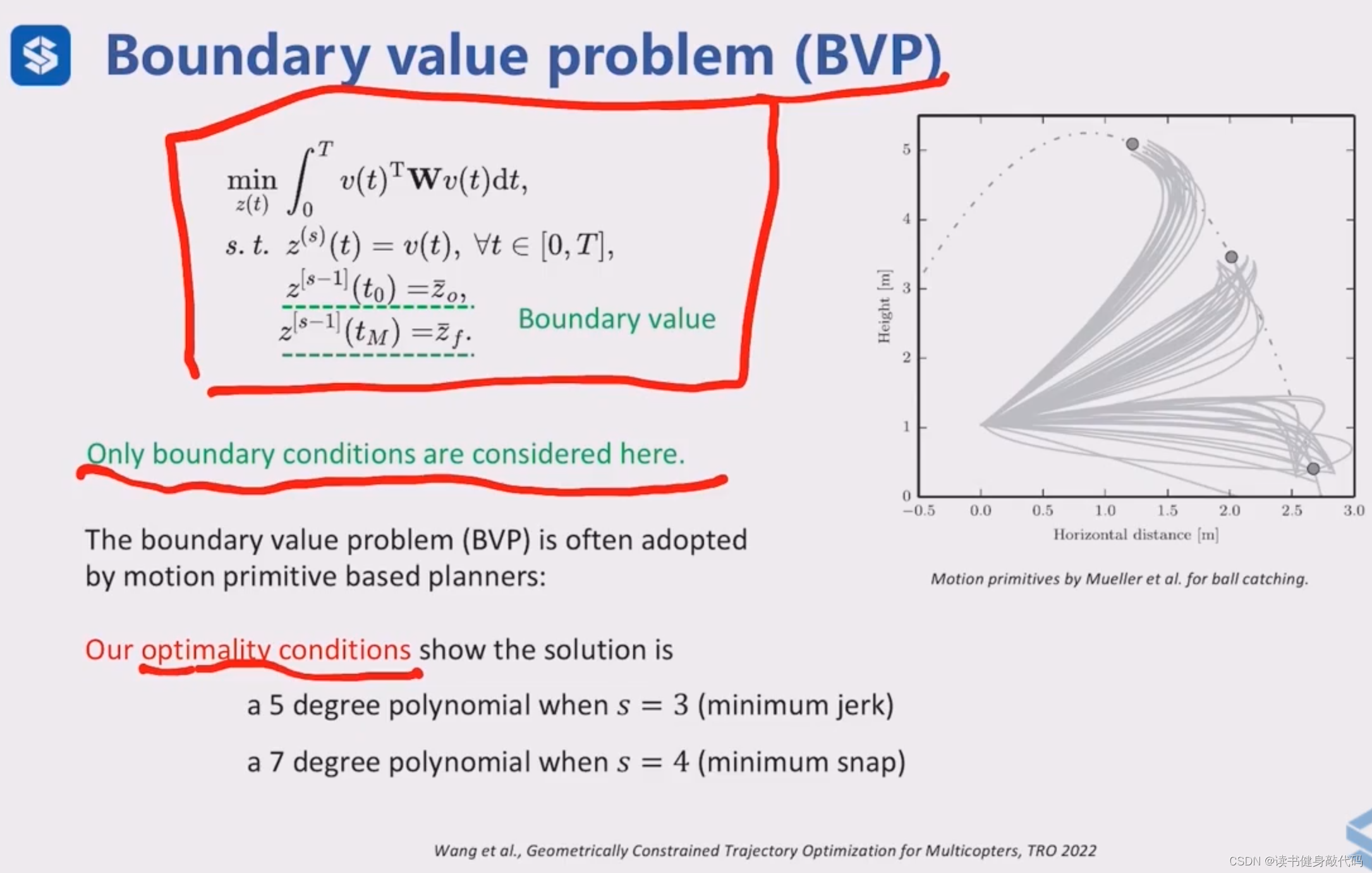
与[13]一样,此处的思路仍然是先只考虑边界约束,不考虑动力学等其他约束来生成一系列primitives,然后再使用约束对生成的primitives进行check,选出最优的。
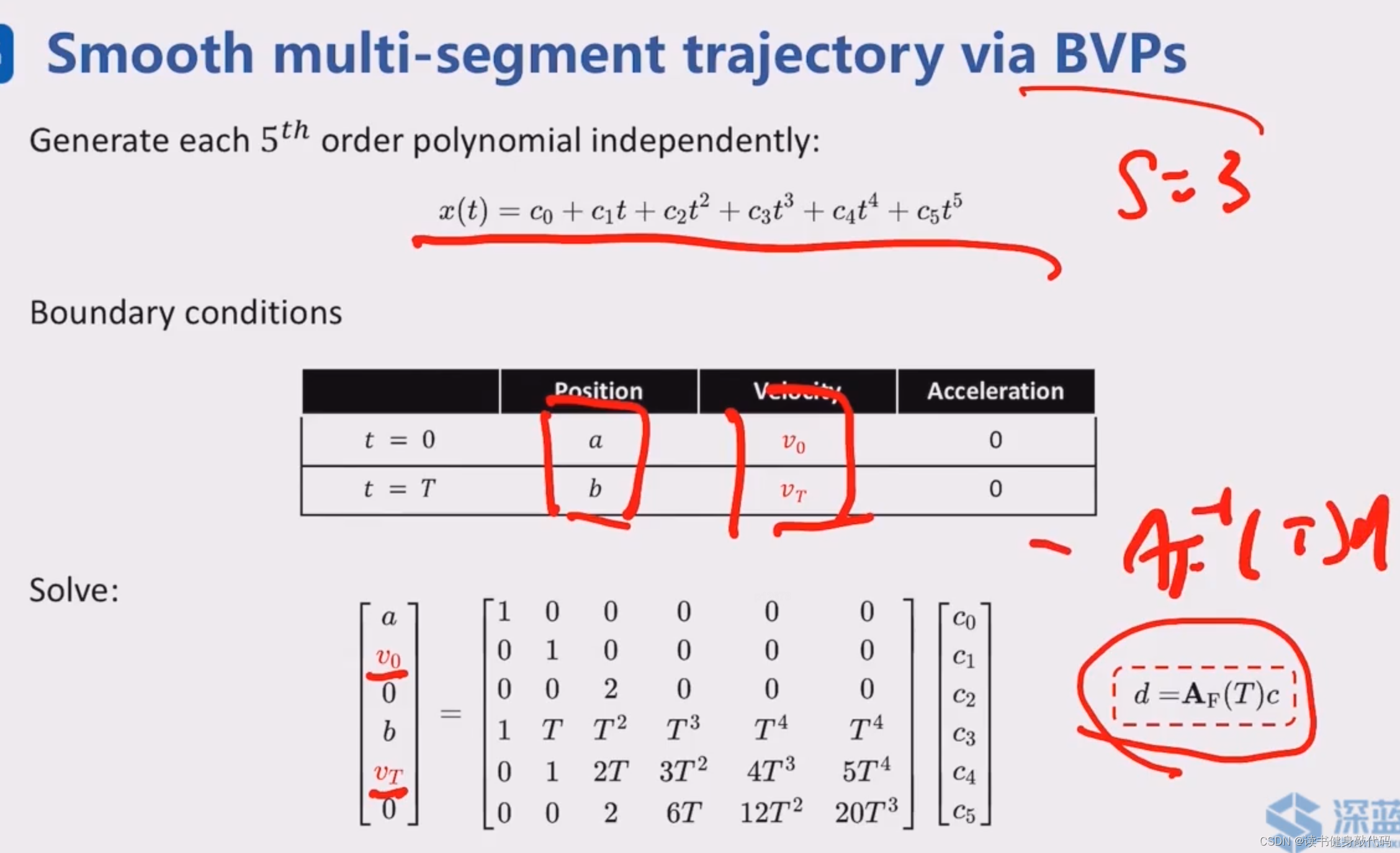
根据边界条件联立方程组,求出 x ( t ) x(t) x(t)的系数,也就求出了 x ( t ) x(t) x(t)的表达式。

可以对一段轨迹进行segmentation,分别构造方程 d = A F ( T ) ∗ c d=A_F(T)*c d=AF(T)∗c,对系数矩阵 A F ( T ) A_F(T) AF(T)求逆可求解每一个seg的BVP,
- 使得整个轨迹看起来更顺滑,且轨迹会满足各个seg求解时的boundary condition,
- 整段轨迹更倾向于匀速运动
- 对于短的seg,时间T较小,矩阵 A F ( T ) A_F(T) AF(T)求逆可能存在数值不稳定的问题,在[14]中给出了 A F ( T ) − 1 A_F(T)^{-1} AF(T)−1的解析形式(也是讲师的工作),可以offline算出解析解的其余部分,online时只带入 t t t的高阶项即可。

如上所示即为 A F ( T ) − 1 A_F(T)^{-1} AF(T)−1的解析形式[13],可以使BVP的求解过程更快。
这样的好处是对于primitives-check这样框架的方法来说,可以使得path的光滑逼近问题计算地更快,效率更高(解多个BVP问题更快)。
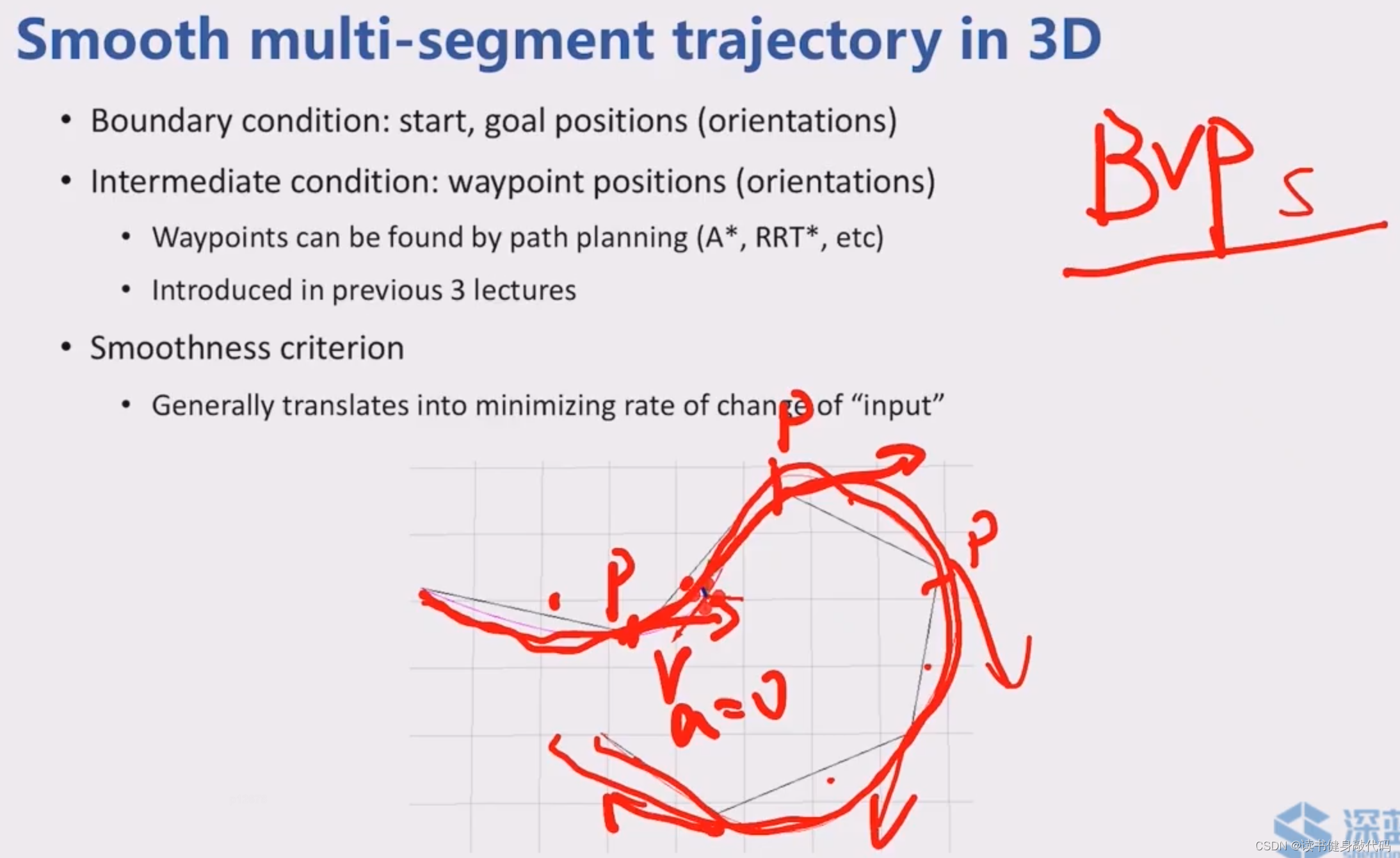
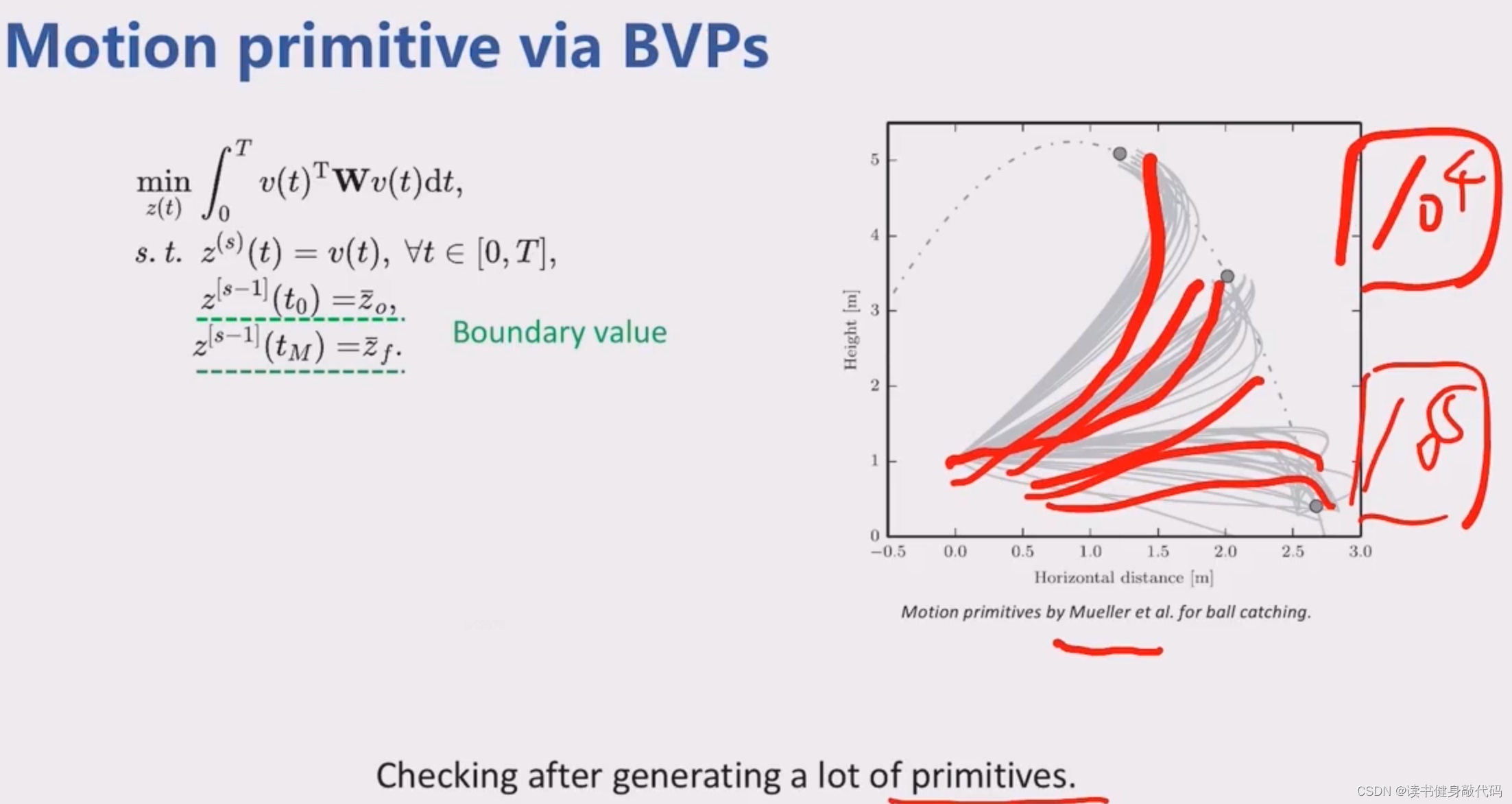
如上即为multi-segment traj的应用[13]。

如何对生成的primitives进行check?且要求是在连续空间而非离散空间中是feasiable的。
每个维度构成一个safe flight corridor,整个primitives都需要在corridor中才算是feasiable的。
结论:把连续时间约束表示为多元多项式,使得多元多项式满足连续时间约束。
如:

表示速度<1,类似的,我们的目标是把其他约束都表示为类似的多元多项式,对多元多项式进行check。
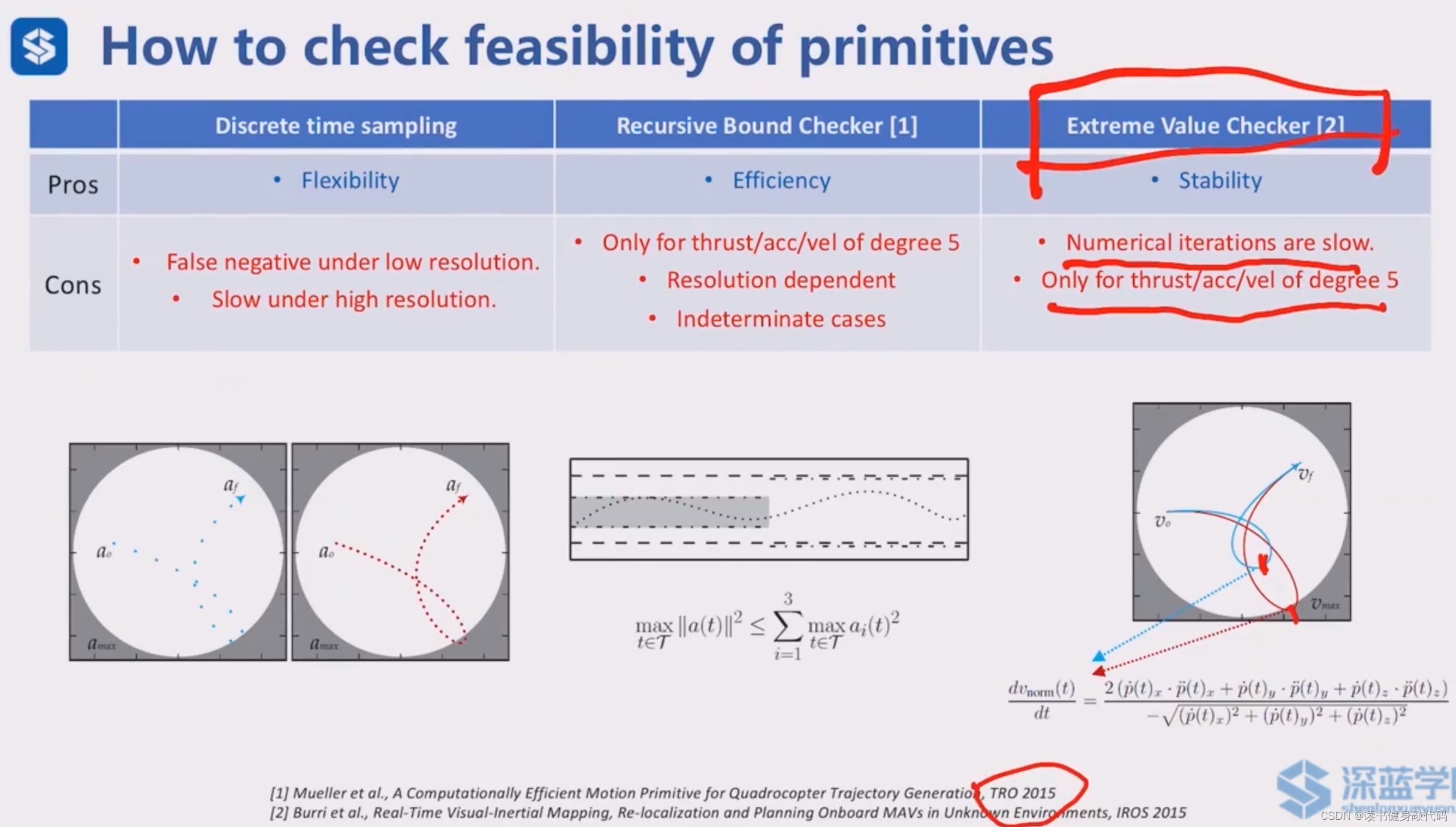
介绍了三种方法:
- 离散时间采样:优点:灵活。缺点:低分辨率容易漏检,高分辨率算的太慢。
- 递归check[13]:只针对thrust/a/v的5次多项式的check,构造一个上界,二次的最大值,有解析解,当T->0时是最tight的upper bound,优点:高效。缺点:仅适用于5次多项式check。
- 极值check[15]:对目标函数求导=0,求出极值,对极值进行check。优点:稳定,对所有场景有效(要么有解析解,要么可以用数值解)。缺点:数值解需要进行迭代,慢。
那么有没有一种通用的解决多元多项式时间约束check的方法?[16]给出(高产!)

检查
G ( p 1 ( i ) ( t ) , p 2 ( i ) ( t ) , p 3 ( i ) ( t ) ) < 0 , ∀ t ∈ [ 0 , T ] \begin{align} \mathcal{G}(p_1^{(i)}(t),p_2^{(i)}(t),p_3^{(i)}(t))<0,\forall t\in[0,T] \end{align} G(p1(i)(t),p2(i)(t),p3(i)(t))<0,∀t∈[0,T]是否成立,转换为在 t ∈ [ 0 , T ] t\in[0,T] t∈[0,T]内 G ( p 1 ( i ) ( t ) , p 2 ( i ) ( t ) , p 3 ( i ) ( t ) ) = 0 \mathcal{G}(p_1^{(i)}(t),p_2^{(i)}(t),p_3^{(i)}(t))=0 G(p1(i)(t),p2(i)(t),p3(i)(t))=0是否有根,如果有根,则式(2)必定不成立。
感觉这篇学术产出都是把问题转换为一个数学问题,然后看在数学领域有没有现成的比较成熟的求解方法,应用到这里,就完成了一项工作。
关于在给定区间内方程是否有根,在数学上有比较成熟的方法: Sturm Theorem
定义 Sturm Sequence,其中Rem()是求 a b \frac{a}{b} ba的多项式除法的余项,同样也是多项式。

定义 V ( t ) V(t) V(t)为 [ 0 , T ] [0,T] [0,T]之间的 g g g值的正负跳变次数,计算方法是 V ( t ) = V ( T ) = V ( 0 ) V(t)=V(T)=V(0) V(t)=V(T)=V(0),上图所示的算例为4次跳变。
先计算出Sturm Sequence的表达式,然后把左边界(这里是-1)带入各个sequence计算出统计符号变换次数,为4;右边界带入sequence计算出符号变化次数为0,则根的个数为4-0=4个,实际 G ( t ) G(t) G(t)通过因式分解也能看出四个根分别为0,1,3,6。
特殊地,如果sequence值出现0,则直接删除0继续进行判断。
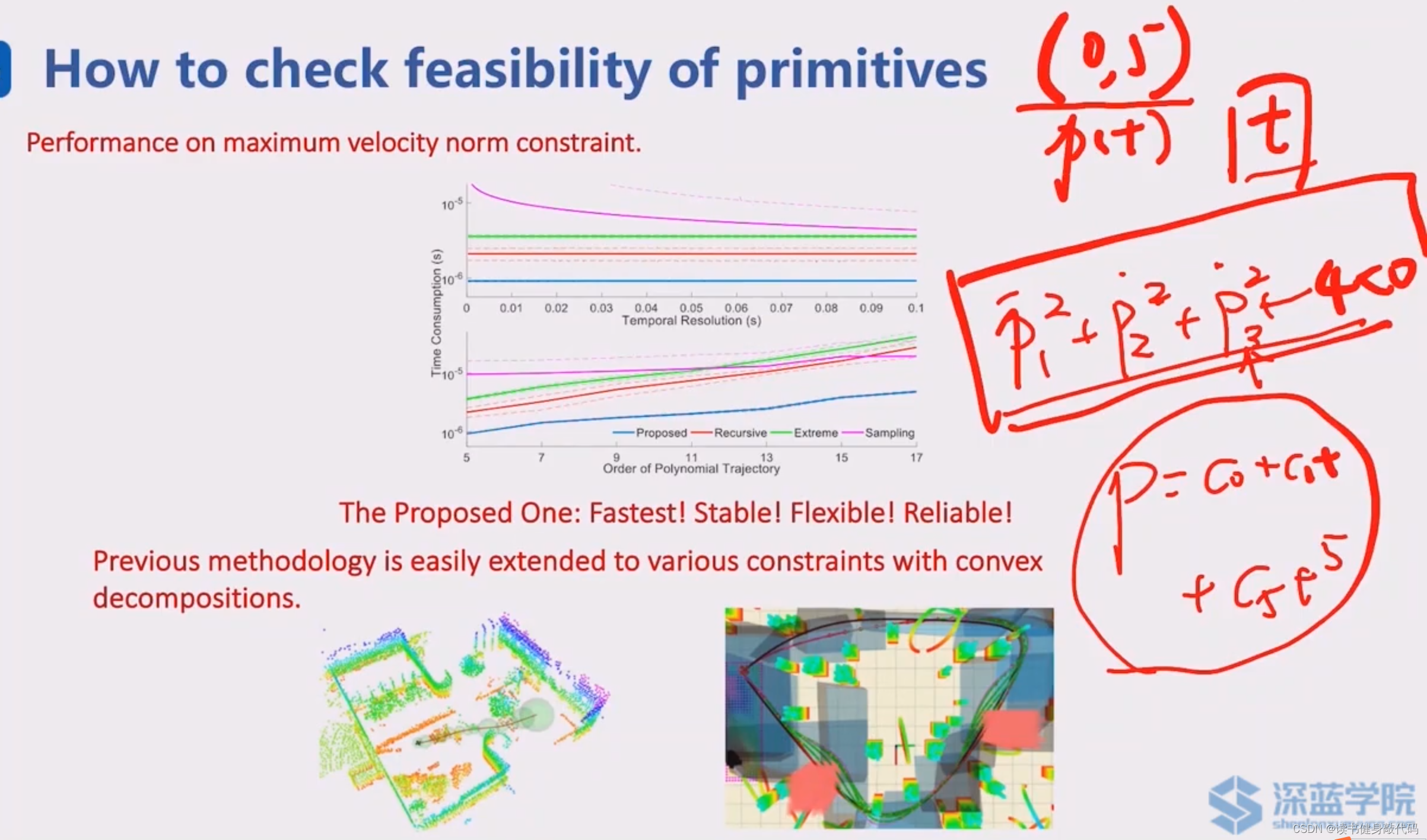
针对具体问题,
- 根据实际约束(如速度)构建如上图所示的不等式,
- 把多项式P带入,计算出不等式 G < 0 \mathcal{G}<0 G<0,
- 将左右边界带入看是否满足 G < 0 \mathcal{G}<0 G<0,若满足,则
- 求取 G \mathcal{G} G的Sturm Sequence,利用上述方法判断根的个数,若不为0,则不满足约束;若为0,则满足约束。
[16]中的方法既快速又稳定,可以拓展到很多凸分解的约束checking。
3.3 Unconstrained Case: BIVP(Multi-segment with intermediate values)
这里讨论的是更加General的问题,
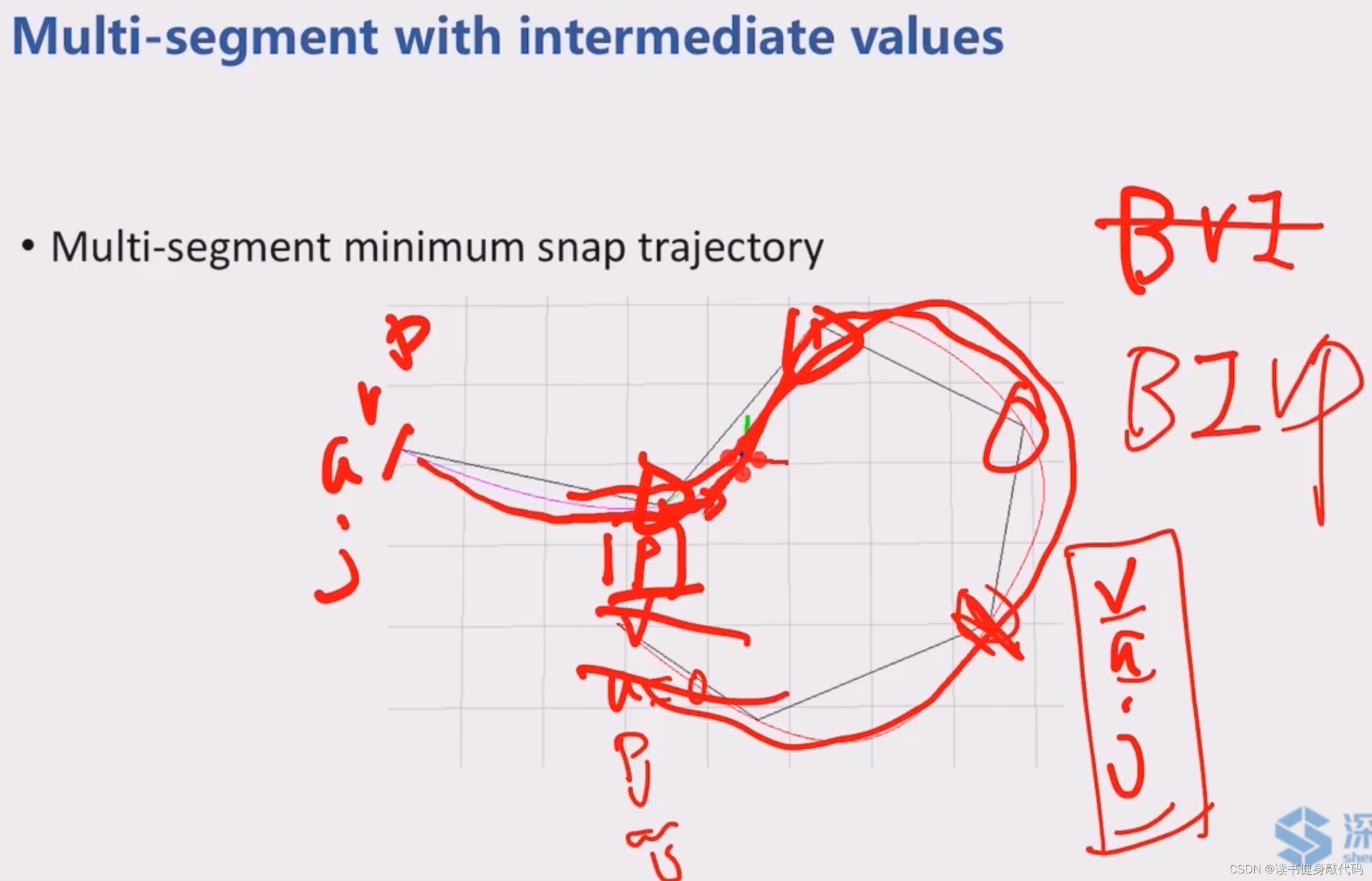

p p p的0阶导为本身,一阶导 v v v,二阶导 a a a,三阶导 j e r k jerk jerk,四阶导 s n a p snap snap,五阶导 c r a c k l e crackle crackle,六阶导 p o p pop pop。
BIVP经常被用于中间状态只有p约束的规划,这样的解具有超出input阶次的更高阶的连续性[12],如优化jerk的energy,solution使得snap连续;优化snap的energy,solution使得pop连续。

如3.2节所述,构造 M C = b MC=b MC=b这样一个方程组,对 M M M求逆即可解出最优解的coeffieient。连cost function的形式都无需构建。
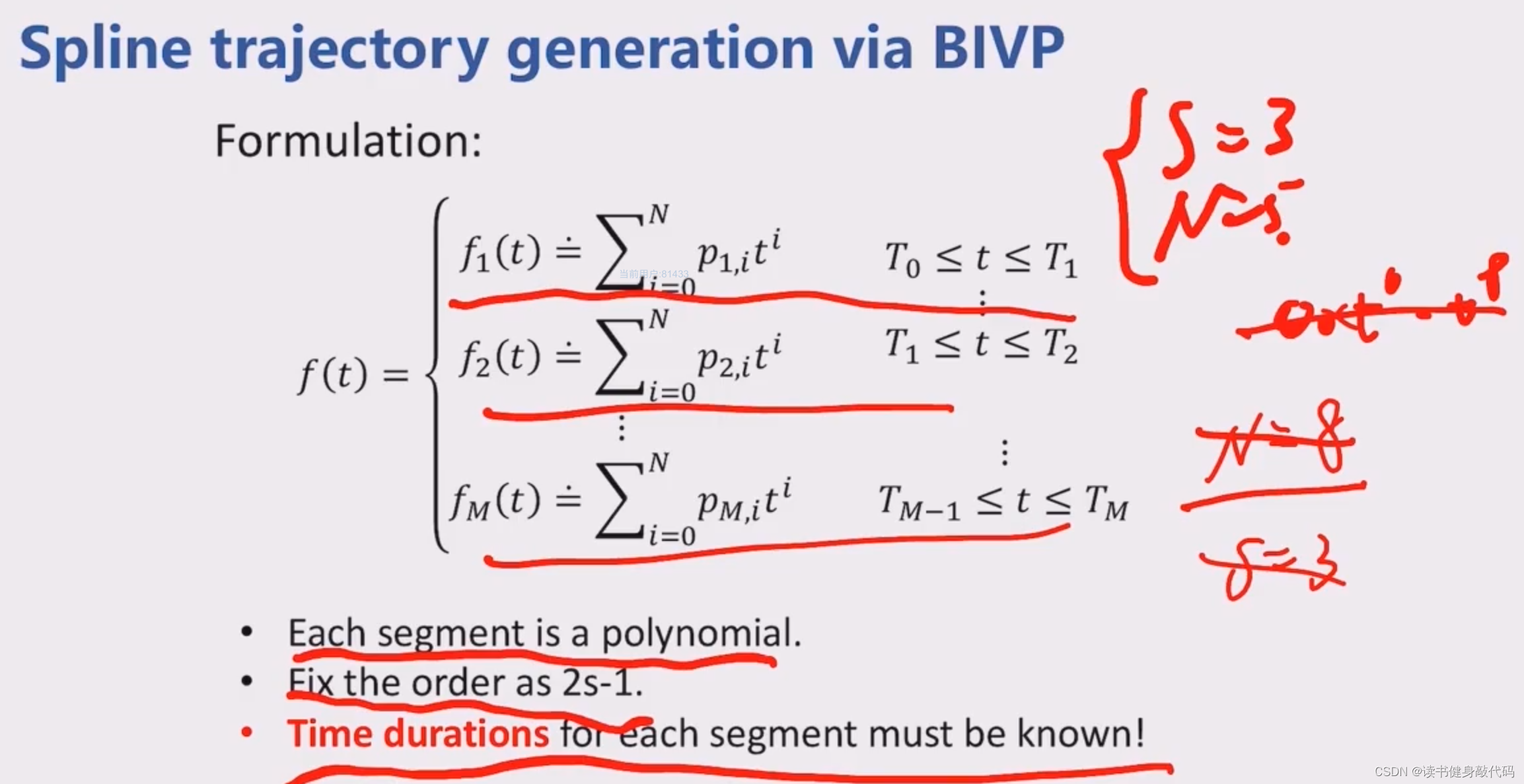
由最优性条件可知,最优解一定是一个2s-1的多项式(课程里面说轨迹不一定是多项式,但最优解一定是多项式(最优解应该是指最优的flat output是多项式,而利用flatness trnasformation转换为state,即轨迹,则state不一定为多项式)),可以分段写出每一段的样条(需要知道每一段的time durations)
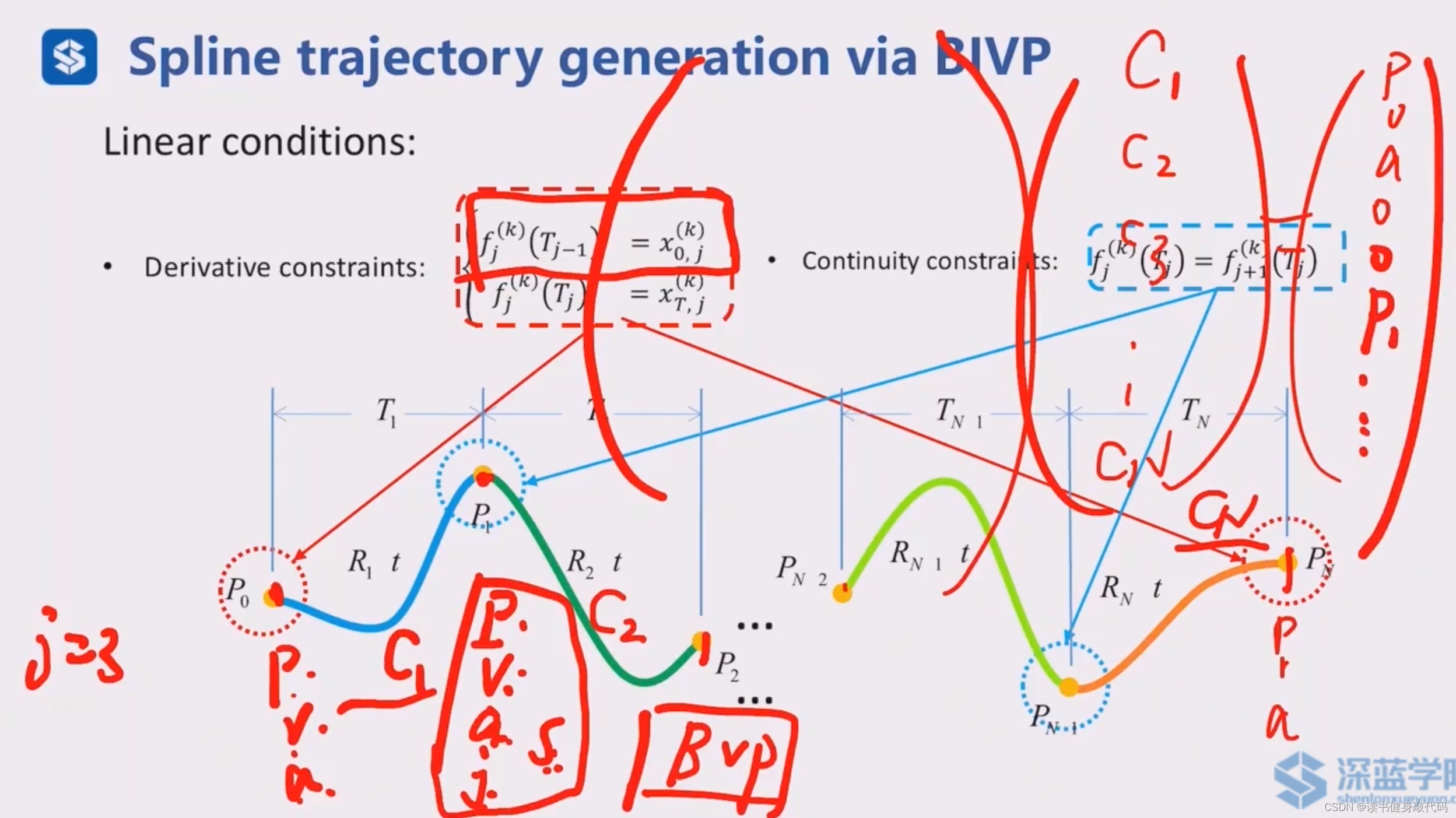
通过线性条件(导数约束和连续性约束)构建方程组进行求解。(这块听不太懂,需要看论文具体才行)
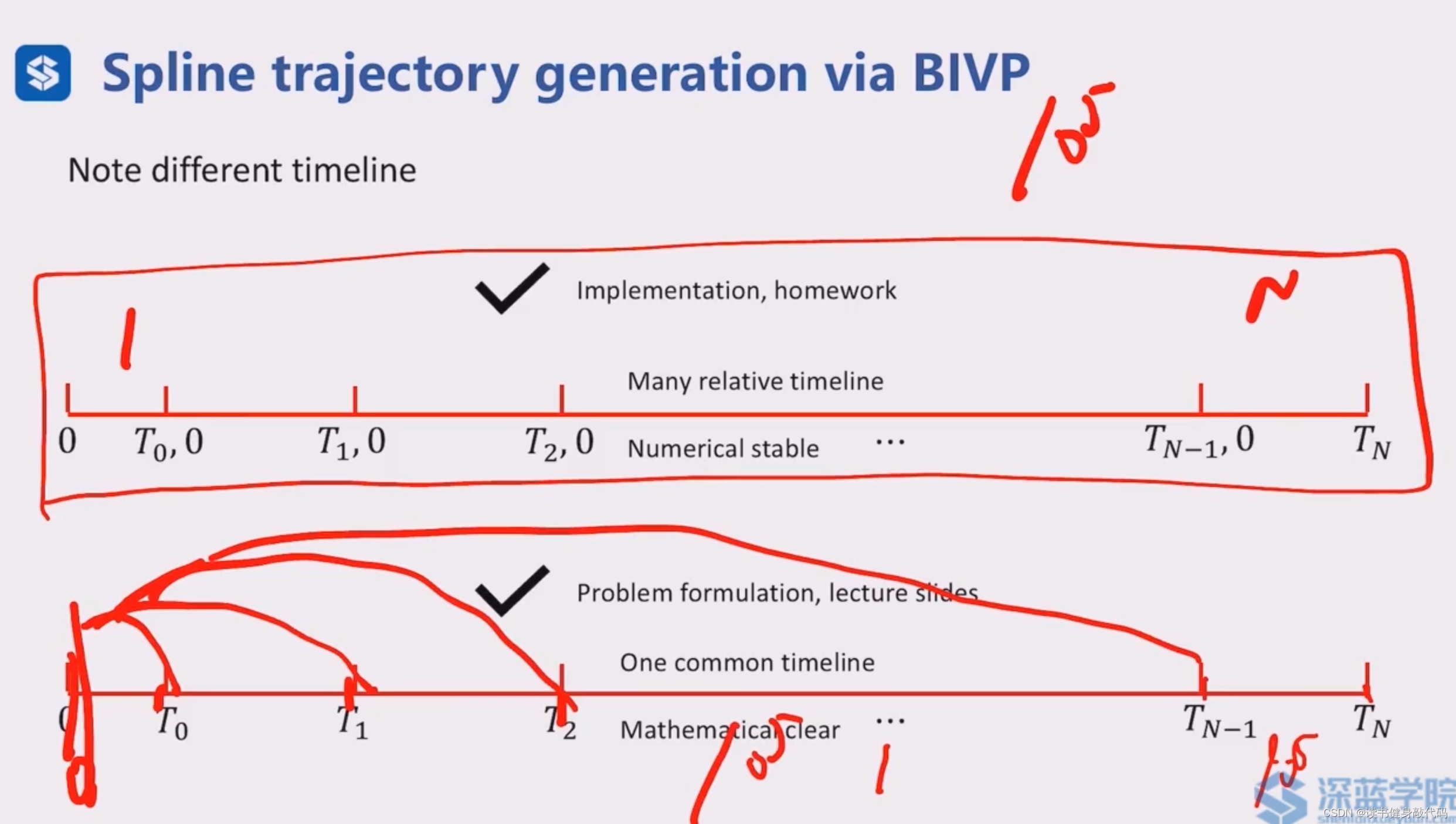
实际实现过程中,通常分别以每一个seg的开始为0时刻,避免了系数矩阵中出现过大的值导致数值不稳定的情况。

写出M之后会发现是一个稀疏的带状矩阵,可以使用稀疏求解器,如PLU分解来求逆,可以在线性的时间内求完成 c c c的求解。
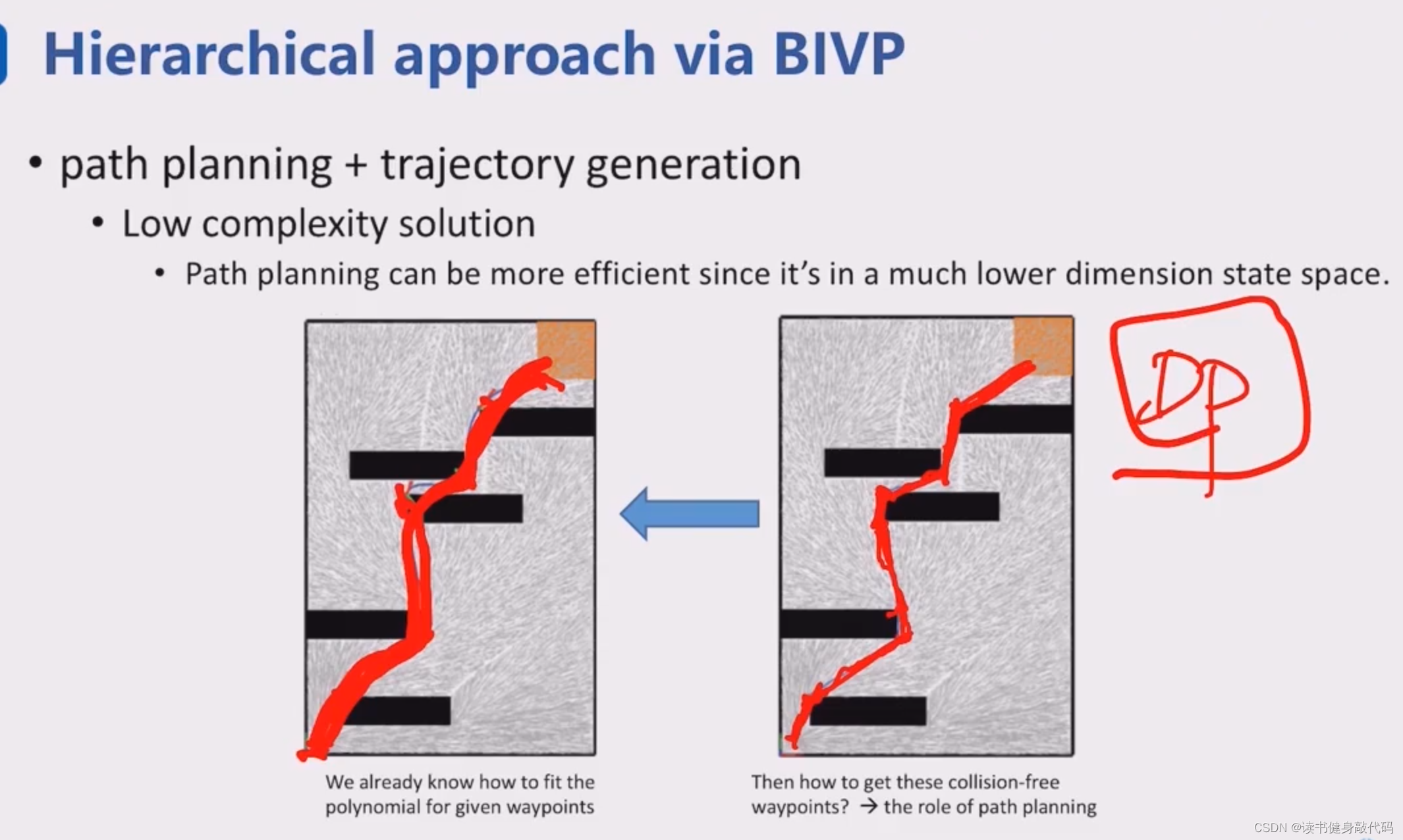
另一种方法是多层次的BIVP,通常是前端的path planning+后端的BIVP
前端用于生成轨迹来获取中间状态,后端使用中间状态构建BIVP进行求解,优化solution。
核心思想:把低维的MP方法用在高维BIVP后端方法的关键点选取上。
前端方法比如:
- 可以使用RRT*这种方法来global地求出一个solution,然后选取solution中的若干点作为中间状态的p,在使用BIVP,
- 使用DP算法求出关键点,然后BIVP。
“Douglas-Peucker算法”(也称为Ramer-Douglas-Peucker算法, 或简称DP算法)这是一个用于减少点数或简化路径的算法,常用于轨迹简化或地图绘制领域。
Douglas-Peucker算法会递归地选择轨迹上的点,以在简化轨迹和保留轨迹形状之间达到平衡。它通过设定一个容差值,然后找到与直线段起点和终点形成最大距离的点。如果这个距离大于容差值,那么这个点会被保留,轨迹会被分成两部分,算法会递归地应用到分割后的两个轨迹上。如果距离小于容差值,则这个点可以被移除。通过这种方式,算法减少轨迹点数,同时尽可能保持轨迹的总体形状。
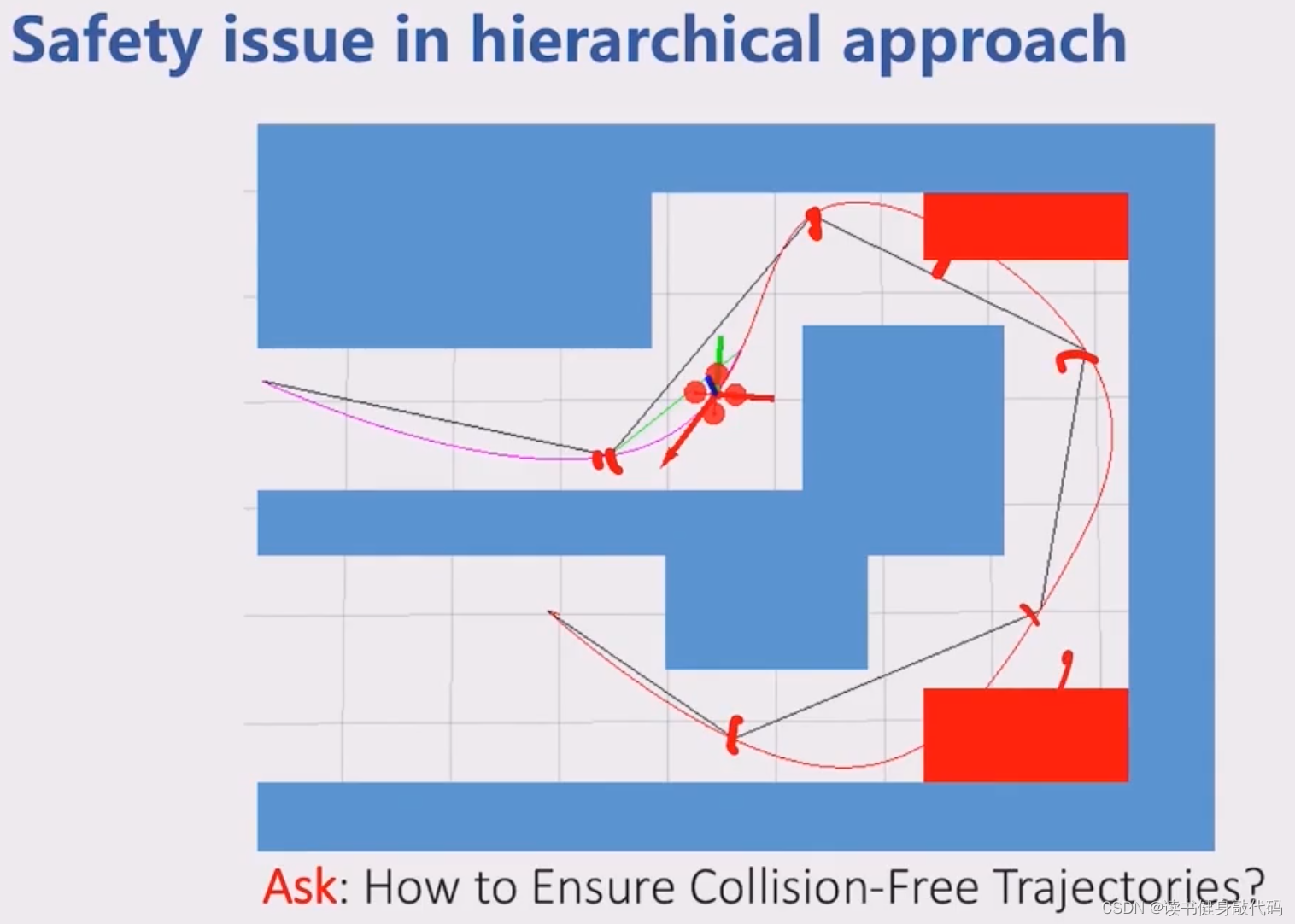
如何保证BVIP的轨迹是collision-free的?

当RRT* 发生碰撞时,尝试把RRT*中间更多的waypoint加入作为关键点给BIVP(来自一几年的IJRR的一篇论文,Bry IJRR 2015 adopted the unconstrained QP formulation)。
把RRT* 这种只能用于低维的motion planning的方法用在决定后端优化的高维的BIVP的关键点选取上。
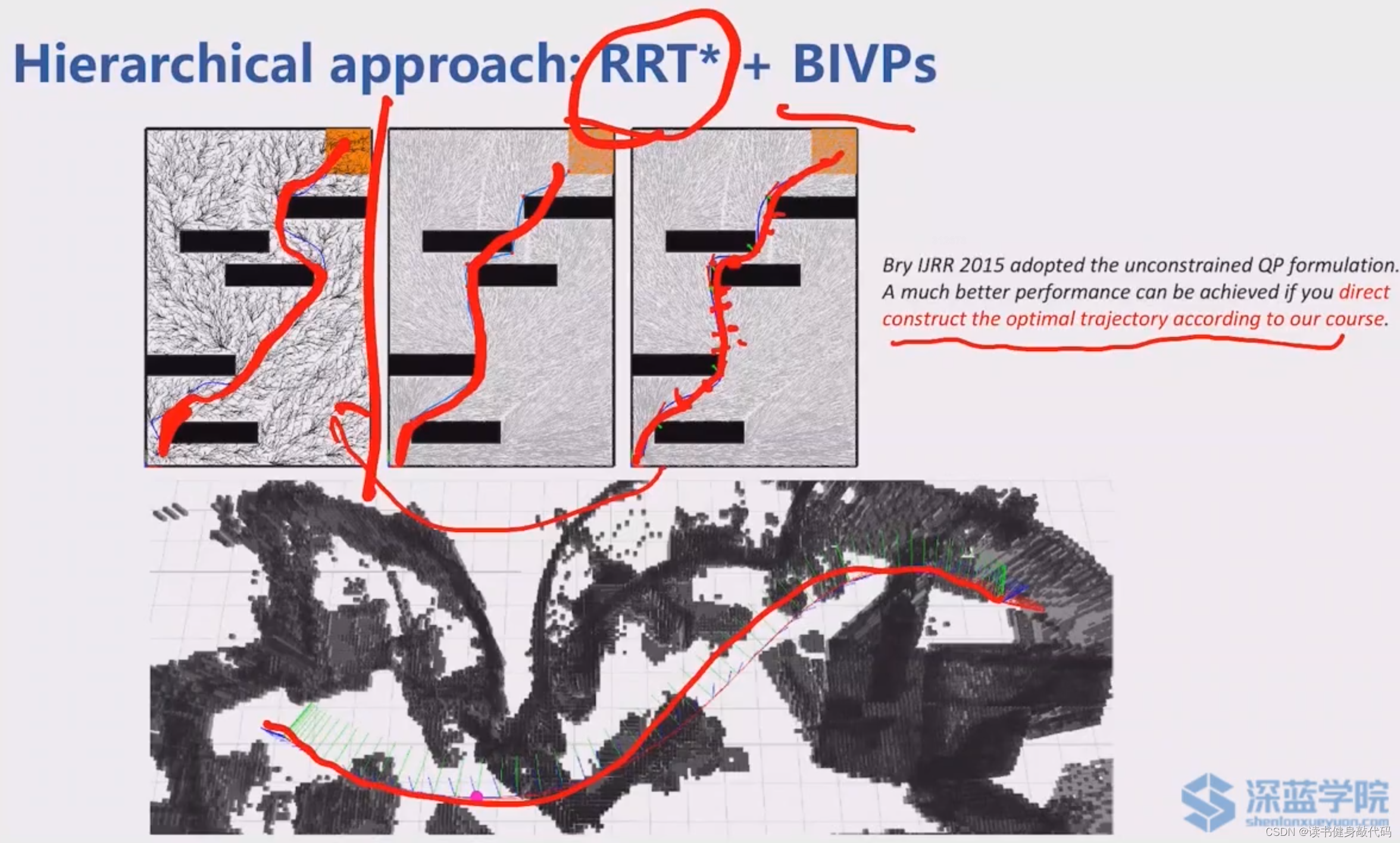
RRT*+BIVPs比Kinodynamic RRT*速度更快,质量更高。
这种RRT*+BIVP的方法能够计算地很快,但是存在一些问题:
- 为了使得最后的solution更优,当障碍物较多时,需要加入更多的waypoint,使得无人机很贴合这些拐角的waypoint才能保证飞行的安全,导致solution不那么顺滑。
- quality static准静态。当无人机飞的足够慢时,可以在任何位置悬停,可以以无限的精度逼近solution,但是这要求是res to res(起始和末尾v,a,高阶导等都为0)。
这类hierarchical的方法的一个研究方向是如何显式地去优化waypoint。
3.4 Constrained Case
考虑free space F \mathcal{F} F和动力学约束 G D ( x , u ) < 0 \mathcal{G}_D(x,u)<0 GD(x,u)<0约束,时间 T T T,轨迹形状等约束的问题。

可以根据上述蓝字部分的思路进行简化:
- 用样条来进行参数化
- 固定 T T T或者allocate大概的时间占比。
- 固定一些基本的约束,而不管底层约束(角速度,推力等)
- 可以提取Configuration space中的一部分,使得我们关心的问题是locally convex,局部地解一些凸优化问题。
3.4.1 Constrained Case: Convex Simplification

如上所示为对costfunction进行局部简化[17],将cost function分成多段,约束分为各个凸多面体。
-
相邻两段之间的连续性约束:
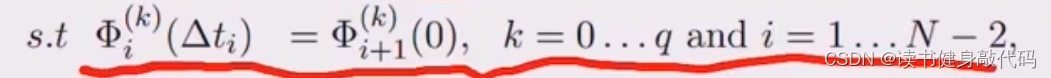
如第1段末尾和第二段开始的p是相等的。 -
boundary value condition,每一段的起始和末尾的状态是指定的
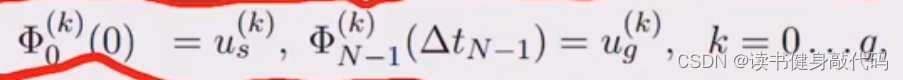
如第1段起始和末尾的pva都指定。需要注意,这里的中间状态waypoint我们是不知道的,需要进行优化。 -
安全约束(与BVP和BIVP最大的不同)

A i T Φ i ( t ) ≤ b i , i = 0 , ⋯ , N − 1 A_i^T\Phi_i(t)\leq b_i,i=0,\cdots, N-1 AiTΦi(t)≤bi,i=0,⋯,N−1
这里 Φ i ( t ) \Phi_i(t) Φi(t)表示 t t t时刻位置,保证飞行安全,可以在每段内进行采样,check每个采样点是否满足安全约束,只要采样足够密,就能够保证安全。最终,安全约束被转换为QP问题。
“QP”(Quadratic Programming,二次规划),这是一类特殊的数学优化问题。在二次规划问题中,目标函数是一个二次函数,同时约束条件可以是等式和/或不等式,这些约束通常是线性的。
。二次规划问题可以表示为以下的标准形式:
目标函数:
min ( 1 2 x T Q x + c T x ) \min \left( \frac{1}{2} x^T Q x + c^T x \right) min(21xTQx+cTx)
约束条件(不等式约束和等式约束):
{ A x ≤ b E x = d \begin{align*} \left\{ \begin{array}{l} Ax \leq b \\ Ex = d \end{array} \right. \end{align*} {Ax≤bEx=d
其中, x x x是决策变量向量, Q Q Q 是一个对称的二次项系数矩阵, c c c 是线性项系数向量, A A A是不等式约束的系数矩阵, b b b 是不等式约束的常数项向量, E E E 是等式约束的系数矩阵, d d d 是等式约束的常数项向量。

如果给定了控制时间T和被积函数的系数 p j p_j pj,则可以把cost function解析地写出。

等式约束(即3.4.1的前两个约束等式):如果想让轨迹经过某个waypoint,则可构建如上等式,将未知的系数 p j , i p_{j,i} pj,i与系数矩阵分离开,即可写出等式约束:
A j p j = d j A_j p_j =d_j Ajpj=dj

上图在每个seg使用了绝对时刻,如果使用相对时刻,则分别为 0 0 0和 T T T。
不等式约束也类似,将待优化的系数 p j , i p_{j,i} pj,i提出,至此cost fucntion和所有的等式、不等式约束均表达出来,下面可以调用凸优化求解器进行求解。

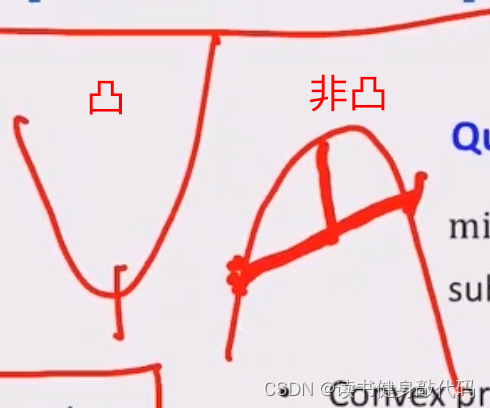
针对凸函数Convex function,如果函数 f ( x ) f(x) f(x)满足
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) \begin{align*} f(\theta x+(1-\theta)y) \leq\theta f(x)+(1-\theta)f(y) \end{align*} f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
则 f ( x ) f(x) f(x)是凸函数。(结合上左图理解,两点连线之间的函数值均在连线的下方)
如果严格满足小于 < < <,则是strictly convex。(当 f ( x ) f(x) f(x)为线性时,等号成立)
且如果该问题的不等式约束是一个凸集合(convex set,集合中任意两点连线均在集合内部,则该集合为凸集合),则该问题是一个凸问题。
如果还存在等式约束,则需要是线性等式约束,该问题才能称之为凸问题。

上图左侧是优化问题的standard form,右侧是凸优化问题的standard form。
大多数问题在formulate时是非凸的,reformulateing problem是一门艺术,没有系统的方法…
针对凸优化,下面介绍general的形式:
Disciplined convex optimization programs (“规范凸优化范式”):

①LP线性规划:cost function,不等式约束,等式约束均为线性。
②对于二次规划(QP)问题,要求系数矩阵 P P P半正定,才能称为凸问题
分别假设 P = 1 2 , P = − 1 2 P=\frac{1}{2},P=-\frac{1}{2} P=21,P=−21,同时设 q = 0 , r = 0 q=0,r=0 q=0,r=0,则目标函数分别为 1 2 x 2 \frac{1}{2}x^2 21x2和 − 1 2 x 2 -\frac{1}{2}x^2 −21x2,前者为凸,而后者非凸,如下所示:
③QCQP(Quadratically Constrained Quadratic Programming,二次约束的二次规划):目标函数是一个二
次函数,同时不等式约束条件也都是二次的(保证系数为半正定)。
④SOCP(Second-Order Cone Programming,二阶锥规划):
目标函数通常是线性的,约束条件可以包括线性约束、二次约束
主要是不等式约束有变化,举例: ∣ ∣ x 2 ∣ ∣ ≤ x 1 ||x_2||\leq x_1 ∣∣x2∣∣≤x1
则图像如下所示,三轴分别为 x 1 , x 2 ( 0 ) , x 2 ( 1 ) x_1,x_2(0),x_2(1) x1,x2(0),x2(1),由于 x 1 ≥ 0 x_1\geq 0 x1≥0,所以在 x 1 x_1 x1正半轴, x 2 x_2 x2模长随着 x 1 x_1 x1增大而增大,呈圆锥形(Second-Order Cone 或ice cream cone),将图像投影到 x 1 x 2 ( 1 ) x_1x_2(1) x1x2(1)平面即为圆锥的投影。

SOCP是最general的凸优化问题形式,①②③均可转换为SOCP,且二阶锥约束使得SOCP能够模拟一些特定的非线性关系,同时保持问题的凸性质,这意味着可以使用高效的算法找到全局最优解。也即LP,QP,QCQP,SOCP均可找到全局最优解。

给出几种凸优化问题的solver:
CVX:http://cvxr.com/cvx/
Mosek:https://www.mosek.com/
OOQP:http://pages.cs.wisc.edu/~swright/ooqp/
GLPK:https://www.gnu.org/software/glpk/
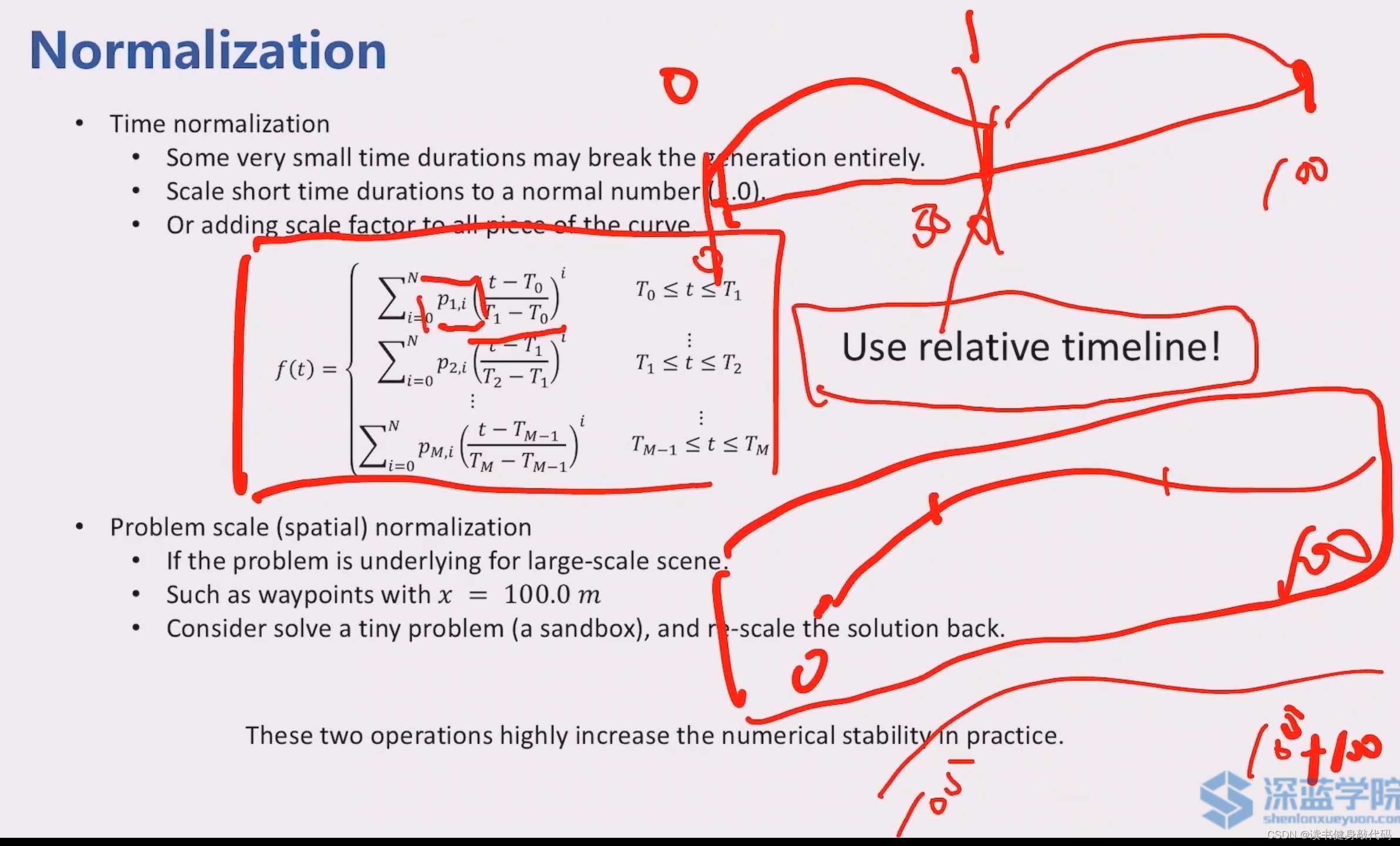
在求解凸优化问题时可能会遇到数值不稳定的问题,可以使用一些Normalization的方法来提高数值稳定性:
- Time normalization:使用相对时间,并进行归一化,归一化为0~1.0之间
- Scale:如果实际数值非常大,可以进行scale,求解一个数值较小的问题,然后再re-scale回去(如 1 0 5 10^5 105这个偏置去掉,求解0~100的问题)。需要注意,有些问题不是scale invarinat的(不同scale对于最终结果有影响),有些是(scale对结果无影响)。
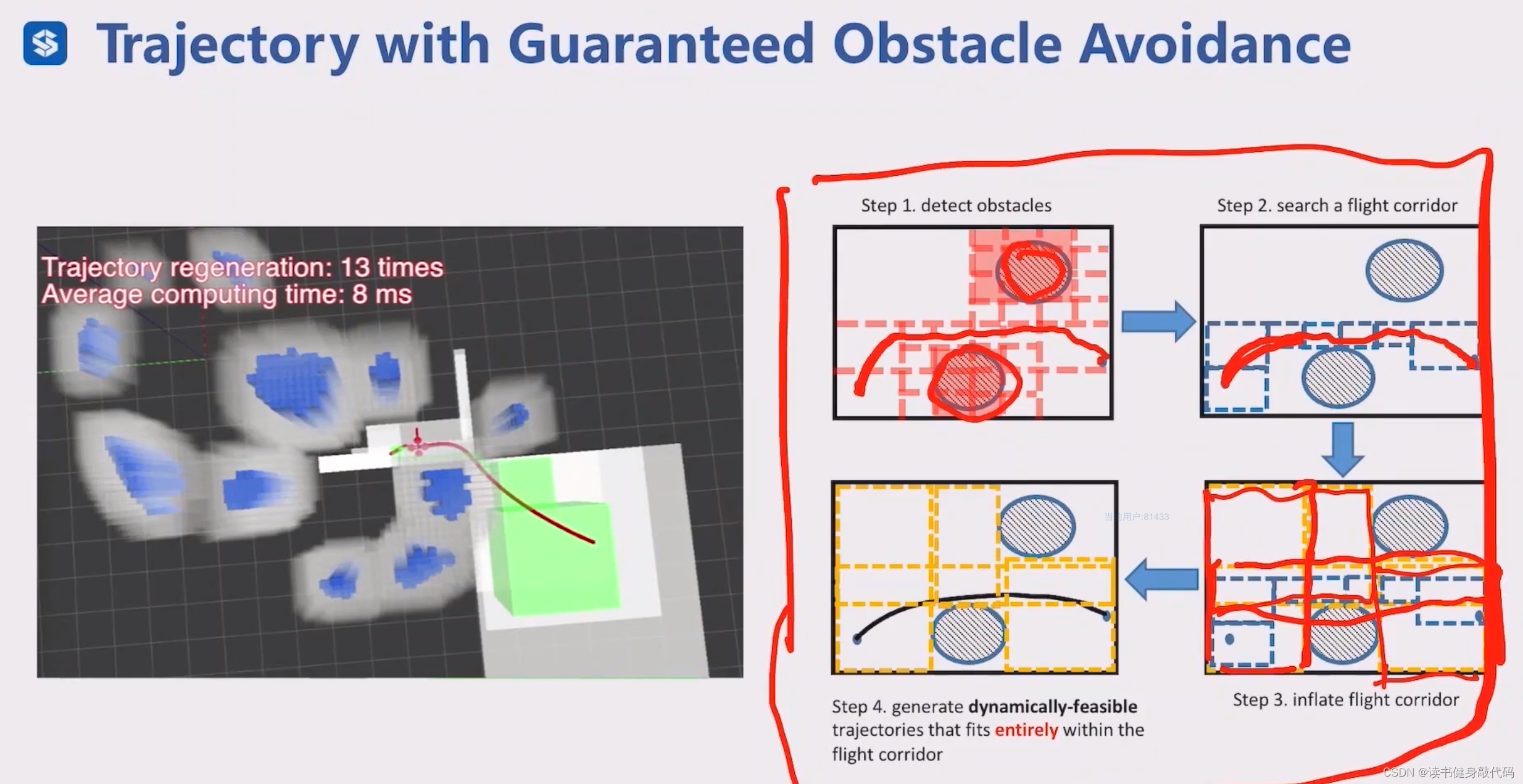
实际的一种生成轨迹的步骤:
- 检测障碍物;
- 生成长方体(一种特殊地凸多面体)的flight corridor;
- 扩展flight corridor,使得其重合区域更大,提升解的质量;
- 在flight corridor中生成feasiable的轨迹。

实现方式:
等式约束,不等式约束(安全边界约束,速度、加速度最值约束)。
3.4.2 Issues of simplification
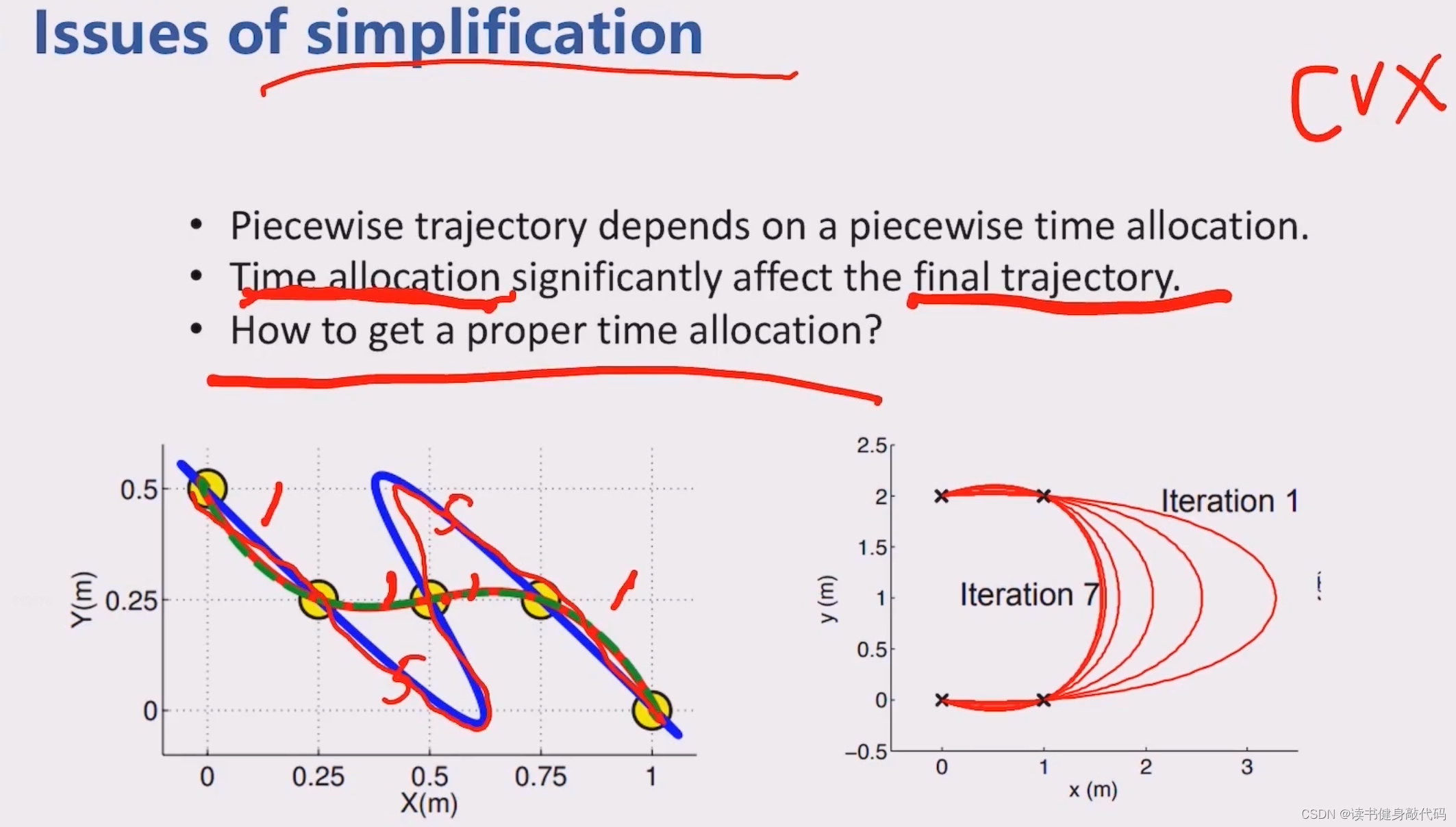
前面没有关于时间 T T T的优化,但是timeallocation对于最终的solutioin影响很大,原因是如果加上时间约束,问题通常是非凸的,无法求解。
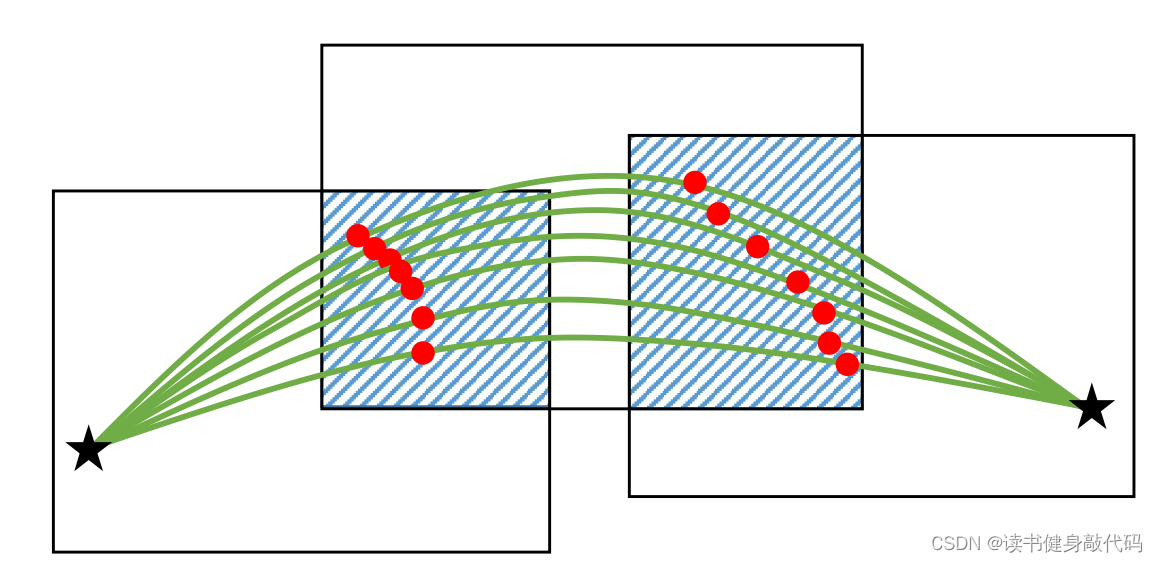
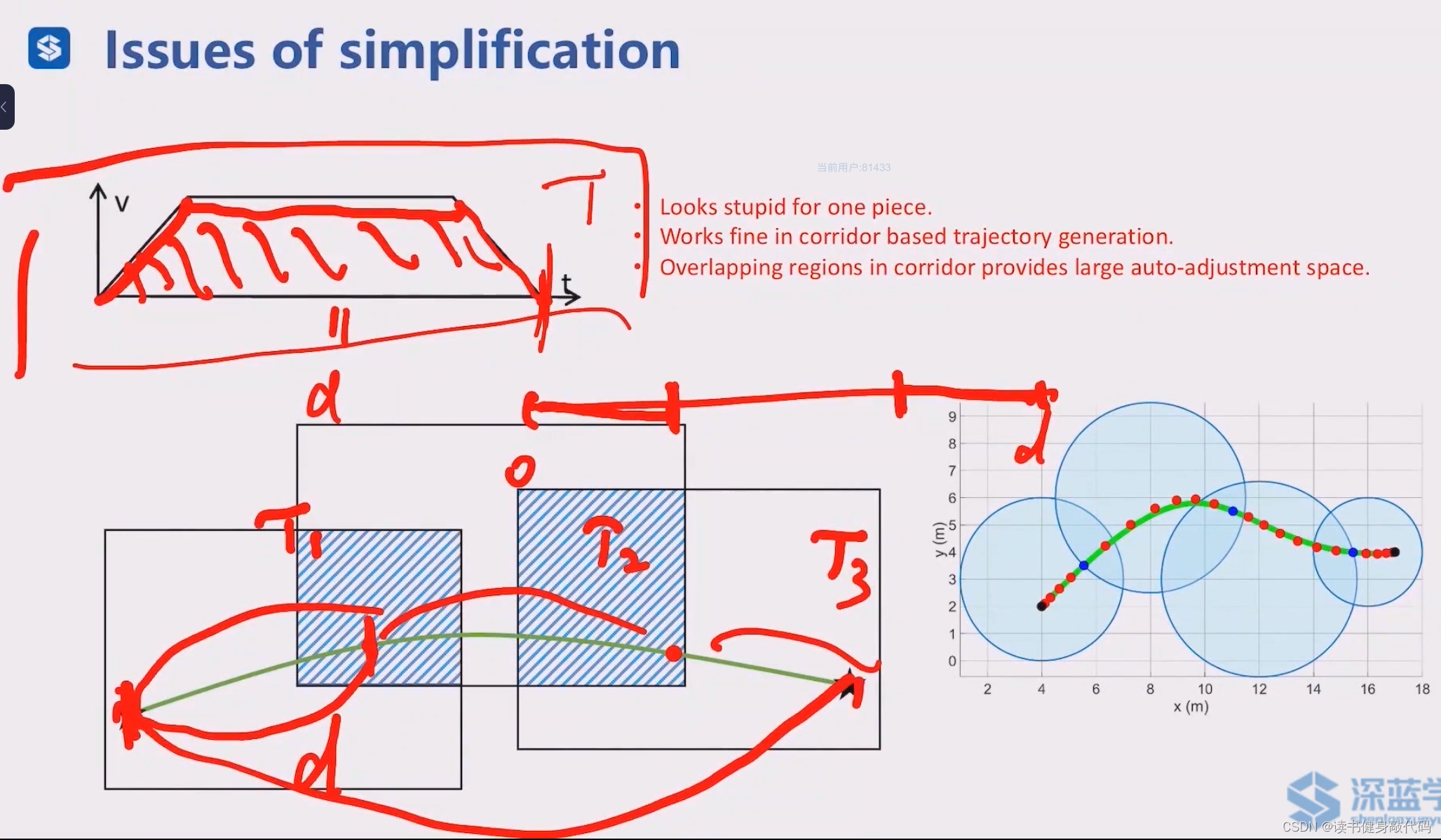
使用flight corridor代替waypoint的好处是flight corridor的overlap部分可以提供更大的优化空间,可能找到更优的解。
一种时间分配的方式是按照加速-匀速-减速的方式分配,只能大概计算出相对的时间占比,但是速度大小无法确定,所以绝对时间 T T T也无法确定。
3.4.3 Constrained Case: Spatial-Temporal Deformation (Brief)
本节简要讨论更加Gneral的轨迹优化,即考虑 F , G \mathcal{F,G} F,G和time allocation。
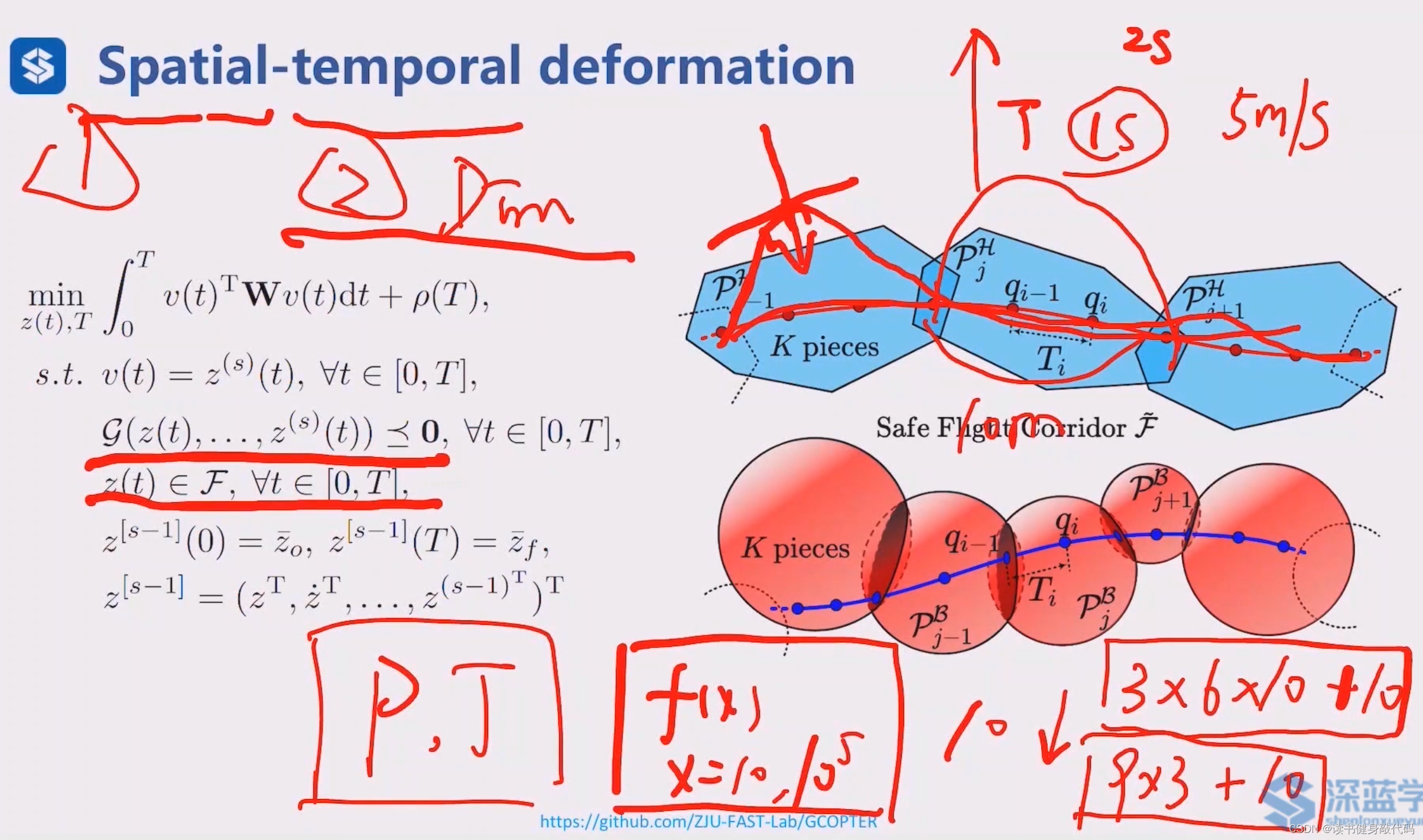
P , T P,T P,T,优化时间序列和空间序列:
- 确定了P和T,通过解BIVP问题可以唯一地确定corridor内的轨迹,轨迹在时间上和空间上的形变打破来满足约束,通过梯度实现,如轨迹超出corridor,向梯度内拉伸使其满足corridor约束
- 可以显著降低优化问题的维度。加速求解。
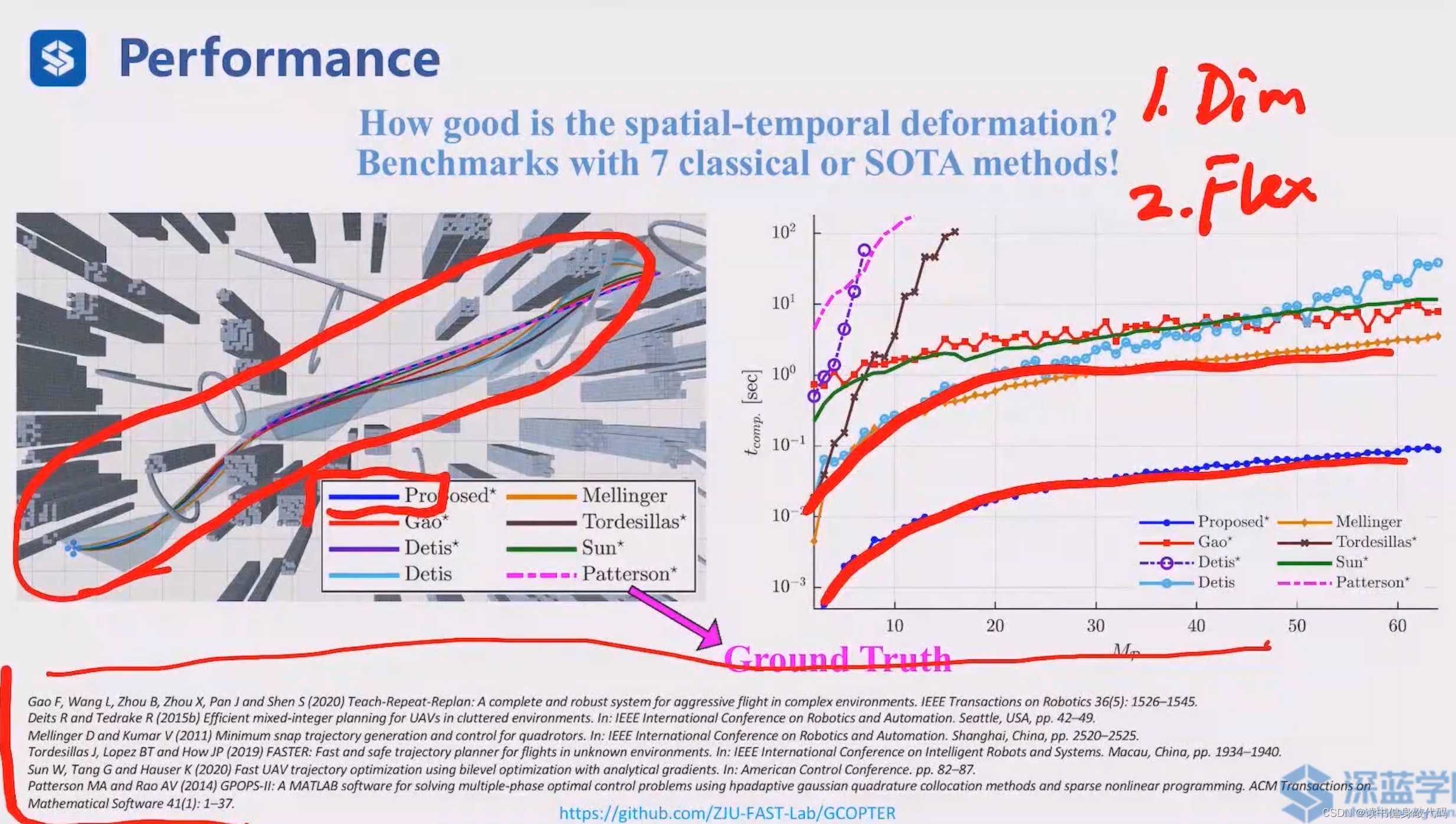
上图所示是FAST-LAB提出的一项工作,计算速度很快,且解质量较高。
同时给出一些多旋翼无人机轨迹优化的参考论文[18~23]
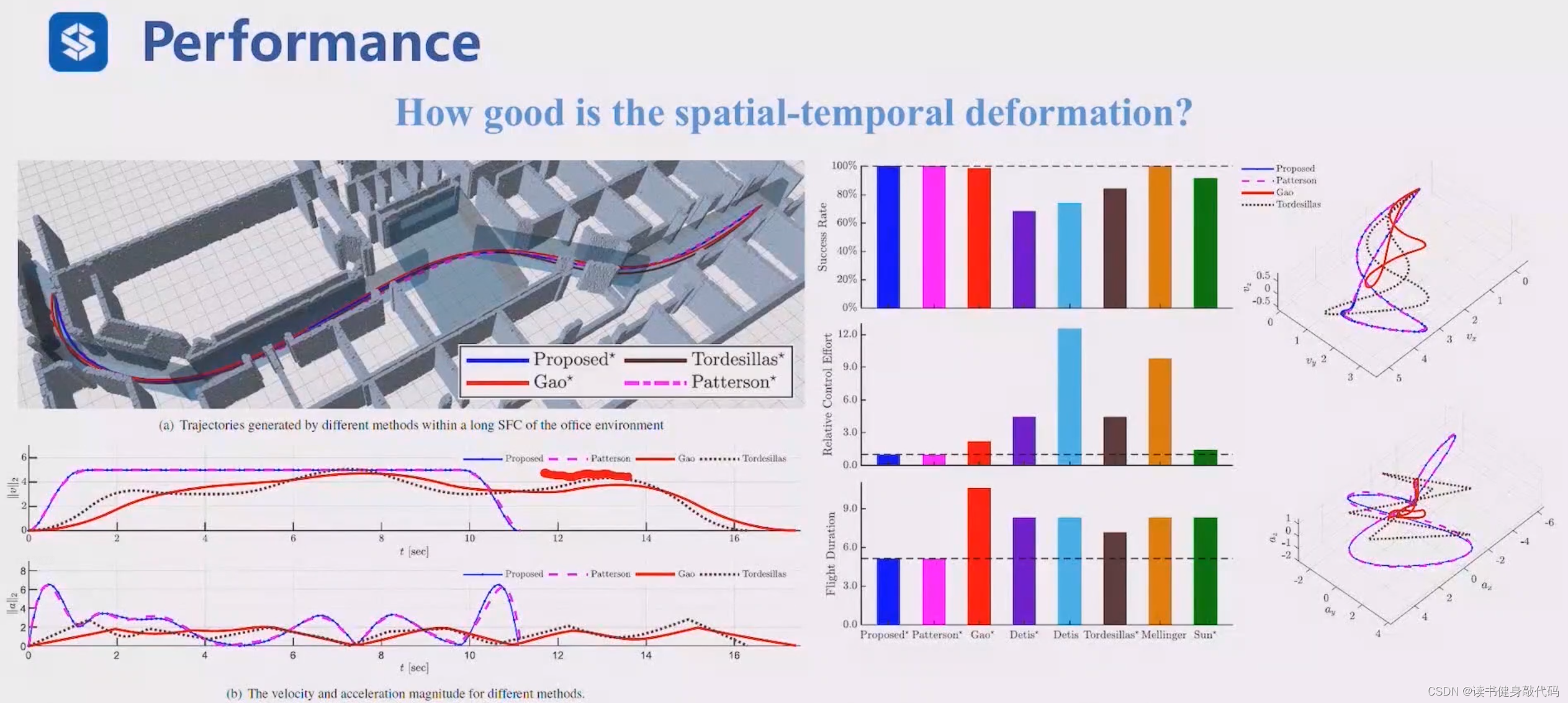
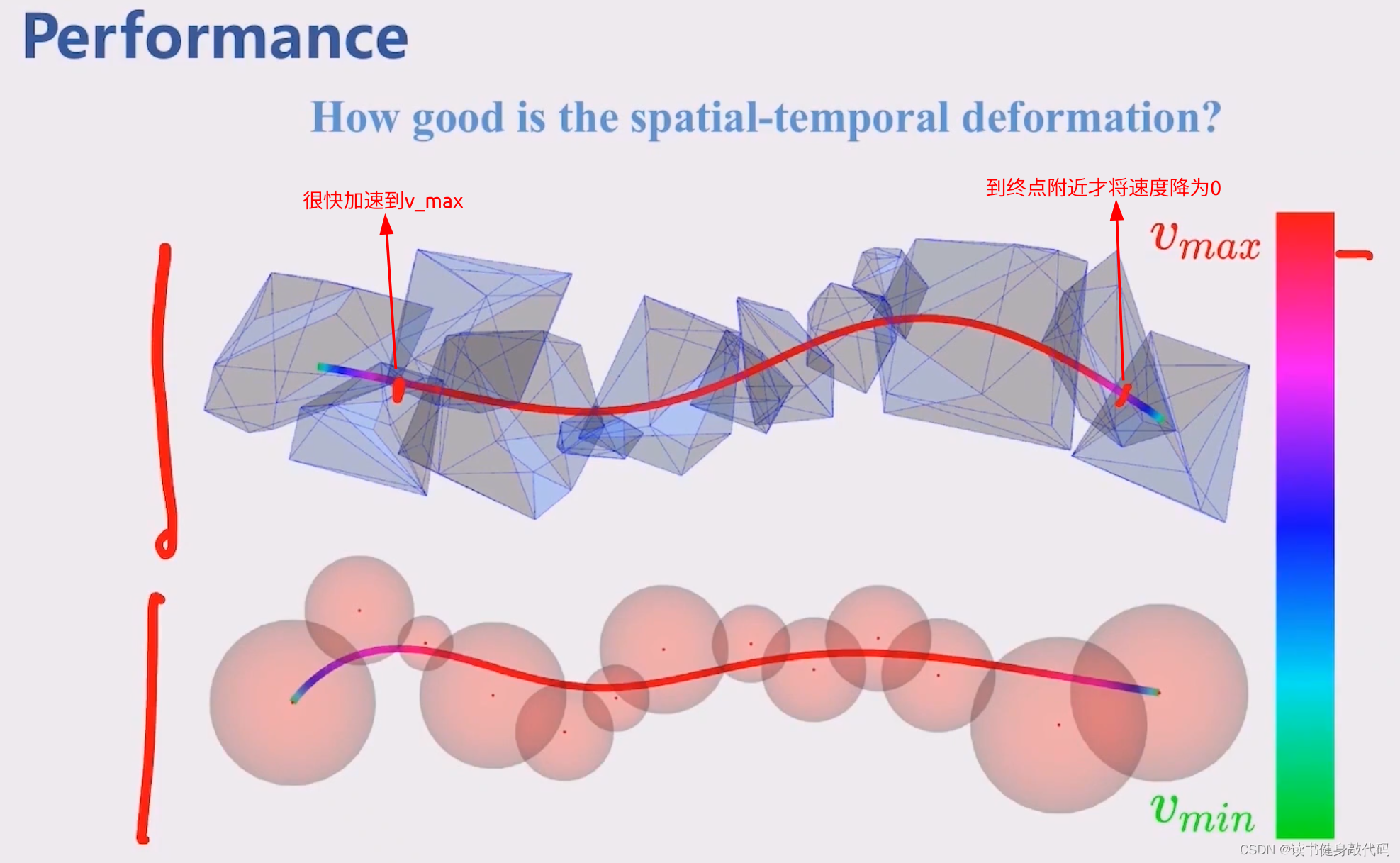
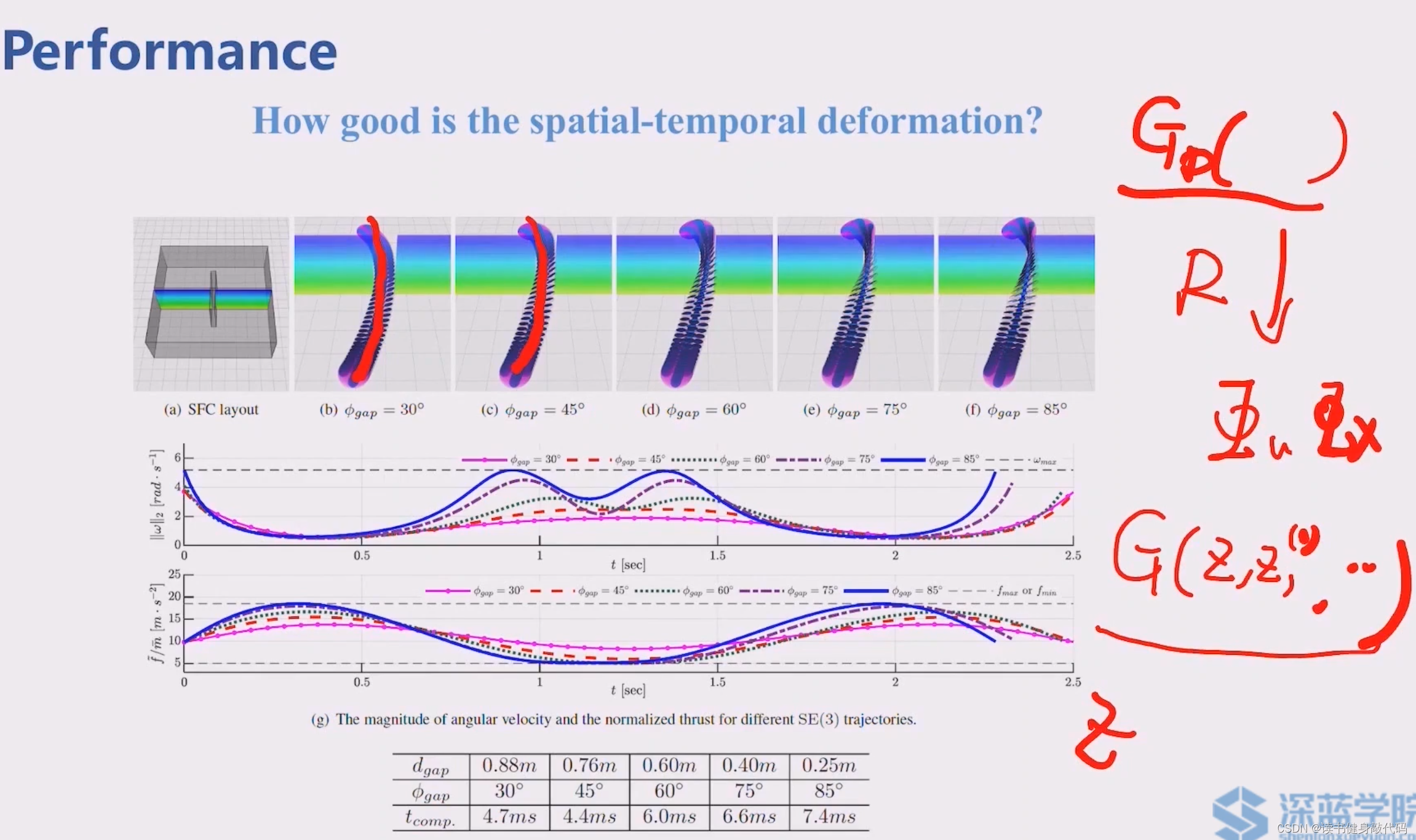
通过flat transformation将施加在state上的约束变换为关于平坦输出 z z z及其高阶导数的多项式约束,集合时空形变能够优化推力和角速度,使drone穿过很窄的缝。
本章讲的较深,需要看论文、继续研究才能理解。
4. Reference
[1] Bry et al., Aggressive flight of fixed-wing and quadrotor aircraft in dense indoor environments, IJRR 2015.
[2] Gao et al., Gradient-based online safe trajectory generation for quadrotor flight in complex environments, IROS 2017.
[3] Zhou et al., Ego-planner: An esdf-free gradient-based local planner for quadrotors. RAL 2020.
[4] Wang et al., Generating Large-Scale Trajectories Efficiently using Double Descriptions of Polynomials, ICRA 2021.
[5] Mellinger et al., Minimum Snap Trajectory Generation and Control for Quadrotors, ICRA 2011.
[6] Faessler et al., Differential Flatness of Quadrotor Dynamics Subject to Rotor Drag for Accurate Tracking of High-Speed Trajectories, RAL 2017.
[7] Ferrin et al., Differential Flatness Based Control of a Rotorcraft For Aggressive Maneuvers. IROS 2011.
[8] Mu et al., Trajectory Generation for Underactuated Multirotor Vehicles with Tilted Propellers via a Flatness-based Method, AIM 2019.
[9] Watterson et al., Control of Quadrotors Using the Hopf Fibration on SO(3), ISRR 2017.
[10] Lee et al., Geometric tracking control of a quadrotor UAV on SE(3), CDC 2010.
[11] Vince, Quaternions for Computer Graphics, Springer 2011.
[12] Wang et al., Geometrically Constrained Trajectory Optimization for Multicopters, TRO 2022.
[13] Mueller et al., A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation, TRO 2015
[14] Wang et al., Generating Large-Scale Trajectories Efficiently using Double Descriptions of Polynomials, ICRA 2021.
[15] Burri et al., Real-Time Visual-Inertial Mapping, Re-localization and Planning Onboard MAVs in Unknown Environments, IROS 2015.
[16] Wang et al., Alternating Minimization Based Trajectory Generation for Quadrotor Aggressive Flight, RAL 2020.
[17] Liu et al., Planning Dynamically Feasible Trajectories for Quadrotors Using Safe Flight Corridors in 3-D Complex Environments, RAL 2017.
[18] Gao F, Wang L, Zhou B, Zhou X, Pan J and Shen S (2020) Teach-Repeat-Replan: A complete and robust system for aggressive flight in complex environments. IEEE Transactions on Robotics 36(5): 1526–1545.
[19] Deits R and Tedrake R (2015b) Efficient mixed-integer planning for UAVs in cluttered environments. In: IEEE International Conference on Robotics and Automation. Seattle, USA, pp. 42–49.
[20] Mellinger D and Kumar V (2011) Minimum snap trajectory generation and control for quadrotors. In: IEEE International Conference on Robotics and Automation. Shanghai, China, pp. 2520–2525.
[21] Tordesillas J, Lopez BT and How JP (2019) FASTER: Fast and safe trajectory planner for flights in unknown environments. In: IEEE International Conference on Intelligent Robots and Systems. Macau, China, pp. 1934–1940.
[22] Sun W, Tang G and Hauser K (2020) Fast UAV trajectory optimization using bilevel optimization with analytical gradients. In: American Control Conference. pp. 82–87.
[23] Patterson MA and Rao AV (2014) GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hpadaptive gaussian quadrature collocation methods and sparse nonlinear programming. ACM Transactions on Mathematical Software 41(1): 1–37.
这篇关于【深蓝学院】移动机器人运动规划--第5章 最优轨迹生成--笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






