[planet] Rudiger Ehlers - Formal Verification of Piece-Wise Linear Feed-Forward Neural Networks

本文主要是介绍[planet] Rudiger Ehlers - Formal Verification of Piece-Wise Linear Feed-Forward Neural Networks，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Title: Formal Verification of Piece-Wise Linear Feed-Forward Neural Networks
Author: Rudiger Ehlers

1 Introduction

2 Preliminaries

Satisfiability solvers: 可满足性(SAT)求解器检查布尔公式是否具有可满足的赋值。该公式通常要求是连词形式，因此由连词连接的从句组成。每个子句都是多个文字中的一个，它们是布尔变量或它们的否定。一个SAT求解器通过连续地建立布尔变量的估值和回溯来操作，每当发现当前的部分估值和子句发生冲突时，为了获得更好的性能，SAT求解器还执行单元传播，其中部分赋值由文本扩展，这些文本是某些条款中尚未被部分估值违反的唯一剩余的文本。此外，现代求解器执行从句学习，其中由其他一些子句的连接所暗示的从句在搜索过程中被懒惰地推断出来，并使用分支启发式选择要分支的变量。大多数现代求解者也执行随机重新启动。有关SAT解决的更多细节，感兴趣的读者请参阅[FM09]。

Satisfiability Modulo Theory Solving: SAT求解器只支持布尔变量。对于可以自然地表示为对其他变量类型的约束的布尔组合的问题，通常采用可满足性模理论(SMT)求解器。SMT求解器将SAT求解器与其他理论的专门决策过程（例如，相对于实数的线性算术理论)结合起来。

3 Efficient Verification of Feed-forward Neural Networks

本文提出了一种新的方法，它结合了：

对神经网络的整体行为进行近似。
基于弹性滤波的线性约束的不可约不可行子集分析。
从部分节点相位估值的可行性检验中推断出可能的安全节点相位选择
对节点相位进行单元传播类推理。我们在本节中描述了这些想法，并在下一节中介绍了实现它们的工具的实验结果。

3.1 Linear Approximation of Neural Network Value Assignment Functions

3.1.1 对ReLU节点的近似

与MILP不同的是，提出了一种近似的描述约束的方法——三角松弛。

在这里插入图片描述

这种方法需要提前知道变量的上下界。对于神经网络的输入节点，比如图像处理中，我们知道它们的范围一般在 $[0, 1]$ 之间。在其他网络中，通常也需要将输入值归一化，在验证的时候也是如此，这可以使我们在网络上使用经典的区间算法。

3.1.2 对MaxPool节点的近似

对于MaxPool节点的近似，我们可以像ReLU节点一样处理，除了我们不需要节点值的上界。令 $c_1,...,c_k$ 为上一层与MaxPool节点相连接的节点的值， $l_1,...,l_k$ 为其下界， $d$ 是节点的输出值。我们可以实例化出下面的线性约束：

见原文第六页第二段

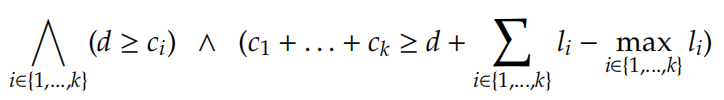
在这里插入图片描述

3.1.3 使近似的结果更加tighten

为了实现这一点我们添加问题 specification $\psi$ 作为约束，并且对于每一个 $\in V$ 求解线性规划问题——最小化 $1 * v$ ，然后对目标函数 $- 1 * v$ 做同样的事。这为每个节点(网络中的ReLU节点)产生了新的更严格的上下限 $[l ， u]$ ，其可用于获得更严格的线性规划。在流程中包含规范可以使我们获得比没有规范时更严格的边界。整个过程可以重复几次：每当获得新的上限和下限时，就可以使用它们建立更紧密的线性网络近似值，从而可以获得新的更严格的上界和下界。

3.2 Search process and Infeasible Subset Finding

给出一组网络中所有ReLU和MaxPool节点的固定相位，检查是否存在一组节点值的分配，同时满足给定的相位和问题规范的约束，可以简化线性规划问题。为此我们通过以下约束扩展了上一节方法构建的线性规划：

对于ReLU节点，每一个 $< = 0$ 的相位，我们添加约束 $v = 0$ 和 $w x + b < = 0$
对于ReLU节点，每一个 $> = 0$ 的相位，我们添加约束 $v < = w x + b$
对于MaxPool节点，每一个相位 $(v^{'}, v)$ ，我们添加约束 $v = v^{'}$

在这里插入图片描述

如果只有一部分节点的相位是固定的（当然正常情况下一定存在一些非确定节点），则仅对固定相位的节点添加约束。如果生成的线性规划不可行，我们可以通过忽略所有对部分估值的扩展。这是通过添加冲突字句来实现的，该字句排除了部分节点相位选择的布尔编码，因此，即使重新启动求解器，仍会保留不可行的原因。

3.2 小节还是比较难以理解的，我读了很多遍，大概有一个浅薄的认识。首先在3.1我们给出了对ReLU（暂时不提MaxPool）的编码方式——三角松弛，在这基础上做出了3.2节的扩展。

假设网络中的隐藏层中一共有且仅有9个ReLU节点，那么根据这9个节点的输入，可以判断出节点的相位，如果输入小于0，则输出一定是0，相位就是负极；如果输入大于0，输出就是 $w x + b$ ，相位就是正极，这也满足3.2中给出的公式的前两条。如果说我们找到一组 $V$ 的变元分配，且满足所有的相位，且满足规范，那么就找到了一组解。

但是现实是，经过区间算术得出的每个节点的上下界不可能直接计算出所有节点的相位。大部分ReLU节点x还是满足l < 0 && u > 0。所以如果我们仅有部分节点的相位是固定的，我们仅给这些固定相位的节点添加3.2中的扩展约束。如果新的线性规划不可行，那么就忽略这些扩展约束。这里的忽略不是通过删除刚刚添加的扩展约束实现的，而是通过添加新的冲突字句实现的，该字句排除了部分节点相位的布尔编码，因此即使重新运行求解器，并不丢失不可行的原因，因为我们每一次回溯都没有删除不可行的部分，而是通过添加冲突字句来抵消不可行的部分。

然而，其实只有很少部分的节点导致了冲突，因此也可以学习较短的冲突字句（这可以使搜索过程更有效）。为了实现这一点，我们使用弹性过滤器。在这种方法中，所有由于节点相位选择而添加的约束都将被松弛变量所削弱，其中每个节点都有一个对应的松弛变量。

当以最小化松弛变量的加权总和为目标再次运行线性规划求解器时，我们将根据节点对冲突的贡献程度对节点进行排名，其中一些节点根本没有贡献（因为它们的松弛变量的值为0）。然后，我们将最大值的松弛变量固定为0，从而使相应的约束变得严格，并重复搜索过程，直到生成的LP实例变得不可行为止。然后我们知道，在此过程中严格执行的节点相位固定装置在一起已经不可行，并且建立了仅包含它们的冲突子句。我们观察到，这些冲突子句比没有应用弹性过滤时要短得多。

3.3 Implied Node Phase Inference during Partial Phase Fixture Checking 部分相位固定装置检查过程中的隐含节点相位推理

在第3.2节中的部分节点固定装置可行性检查步骤中，我们使用了一个线性规划求解器。然而，除了弹性滤波步骤外，我们还没有使用优化函数，因为它不需要检查部分节点固定装置的可行性。

3.4 Detecting Implied Phases 推断未知节点

每当SAT求解器固定了一个新的节点相位时，被选中的那些相位有可能一起推断出其他节点的相位。

3.5 Overview of the Integrated Solver

为了总结本节，让我们讨论如何组合本文中提出的技术。算法1显示了总体方法。在第一步中，计算所有节点值的上界和下界。然后，求解器为 SAT 变量准备了部分空的估值和一个空的额外列表，其中存储了本节提出的 LP 实例分析步骤所产生的额外子句。SAT 实例用强制每个 ReLU 节点和每个 MaxPool 节点恰好选择一个阶段的子句来初始化。（使用单热编码）。

在算法的主循环中，第一步是执行SAT解决的大多数步骤，例如单元传播，冲突检测和分析等。我们假定部分估值始终由决策级别标记，以便在需要时也可以执行回溯。此外，来自Extra的其他子句被混合到SAT实例ψ中。这是分步进行的，因为附加条款可能会触发单元传播，甚至引发冲突，因此需要急切处理。在第12行中，将多余的所有子句都混合到ψ中，并可能通过隐含文字扩展了部分赋值p时，在第12节中介绍了这种方法。应用3.4。如果它返回新的隐含文字（以附加子句的形式），则SAT解决步骤11中的步骤将处理它们。这是因为已经存在于ψ中的子句可能导致新推断的文字上的单位传播，这是有道理的，因为每个其他文字都会使网络行为的线性近似值更加严格（并可能导致检测到其他隐式文字）。仅在推断出所有节点相位后，才检查p在线性逼近中的可行性（第14行）。

此检查有两个不同的结果：如果LP实例不可行，则将生成新的冲突子句，因此不满足第15行的条件。然后，在这种情况下，算法在第11行继续。否则，执行SAT求解器的分支步骤。如果p已经是一个完整的评估值，则此时我们知道该实例是可满足的，这是因为刚刚执行的CheckForFeasibility函数对一个不是近似的LP问题进行了操作，而是捕获了网络的精确行为。否则，通过将变量b设置为true的决定来扩展p（对于SAT解算器的变量选择启发式方法选择的某些变量）。每当这种情况发生时，我们都会使用普通的SAT求解器来检查部分评估是否可以扩展到满足ψ的评估。情况并非如此，可能无法通过第11行中的单元传播检测到，因此进行急切的SAT检查是有意义的。在发生冲突的情况下，b的值会被取反，无论如何，算法都会继续搜索。

在这里插入图片描述