大学生课程|统计基础与python分析3|实战：不同行业工龄与薪水的线性回归模型（免费下载所有课程材料）

本文主要是介绍大学生课程|统计基础与python分析3|实战：不同行业工龄与薪水的线性回归模型（免费下载所有课程材料），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

此系列为基础学习系列，请自行学习，课程资源免费获取地址：

https://download.csdn.net/download/weixin_68126662/88866689

目录

此系列为基础学习系列，请自行学习

1.读取数据

2.绘制离散点图

3.模型搭建

4.模型可视化

5.线性回归方程构造

6.模型优化

---

久菜盒子工作室：大数据科学团队/全网可搜索的久菜盒子工作室 我们是：985硕博/美国全奖doctor/计算机7年产品负责人/医学大数据公司医学研究员/SCI一区2篇/Nature子刊一篇/中文二区核心一篇/都是我们 主要领域：医学大数据分析/经管数据分析/金融模型/统计数理基础/统计学/卫生经济学/流行与统计学/ 擅长软件：R/python/stata/spss/matlab/mySQL

团队理念：从零开始，让每一个人都得到优质的科研教育

点点关注，一起成长，会变更强哦

本次责任编辑：久菜老师

1.读取数据

# 读取数据import pandas as pddf = pd.read_excel('IT行业收入表.xlsx')# 自变量要构造成二维结构x = df[['工龄']]  # 读出来是一个DataFrame# 因变量一维结构即可y = df['薪水']  # 读出来是一个Series

2.绘制离散点图

# 绘制离散点图from matplotlib import pyplot as plt# 用于正常显示中文plt.rcParams['font.sans-serif'] = ['SimHei']plt.scatter(x, y)plt.xlabel('工龄')plt.ylabel('薪水')plt.show()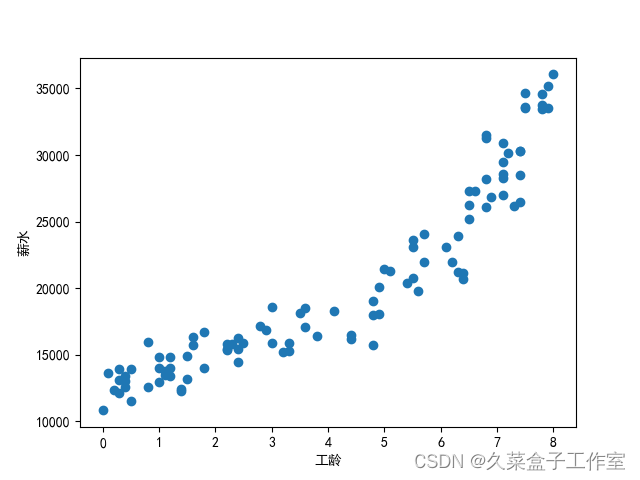

3.模型搭建

# 模型搭建from sklearn.linear_model import LinearRegressionregr = LinearRegression()regr.fit(x, y)  # x需要是一个二维结构形式， y需要是一个一维结构形式；如果x是一个一维结构形式，会出错

4.模型可视化

# 模型可视化# x是一个DataFrame，x.values转成数组，才能被plot()函数读取# plt.plot(x, regr.predict(x), color='red')，即x没有values，会出错plt.scatter(x, y)plt.plot(x.values, regr.predict(x), color='red')plt.xlabel('工龄')plt.ylabel('薪水')plt.show()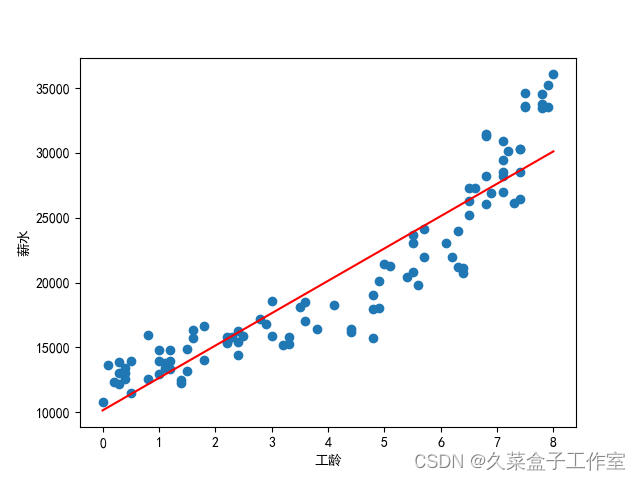

5.线性回归方程构造

# 线性回归方程构造print('系数a：' + str(regr.coef_[0]))print('截距b：' + str(regr.intercept_))

显示：

系数a：2497.1513476046866

截距b：10143.131966873787

6.模型优化

一元二次线性回归：y = ax^2+bx+c

# 引入多次项的模块PolynomialFeaturesfrom sklearn.preprocessing import PolynomialFeatures# 设置最高次项为二次项，为生成二次项数据（x^2）做准备poly_reg = PolynomialFeatures(degree=2)# 将原有的x转换为一个新的二维数组x_，该二维数组包含新生成的二次项数据（x^2）和原有的一次项数据（x）x_ = poly_reg.fit_transform(x)# 获得一元二次线性回归模型regr = LinearRegression()regr.fit(x_, y)# 一元二次线性回归模型可视化plt.scatter(x, y)plt.plot(x.values, regr.predict(x_), color='red')plt.xlabel('工龄')plt.ylabel('薪水')plt.show()# 一元二次线性回归方程构造print('系数a：' + str(regr.coef_))  # 获取系数a、bprint('截距b：' + str(regr.intercept_))  # 获取常数项c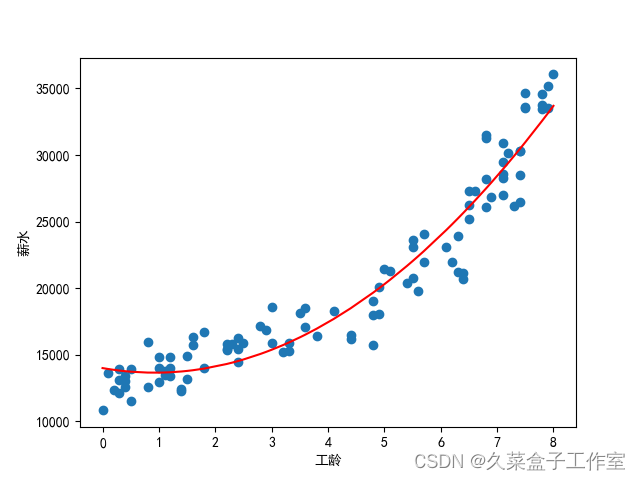

[   0.         -743.68080444  400.80398224]

13988.159332096886

注意：

第一行，第一个是x^0的系数，第二个是x^1的系数，第三个是x^2的系数

第二行，常数

这篇关于大学生课程|统计基础与python分析3|实战：不同行业工龄与薪水的线性回归模型（免费下载所有课程材料）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---