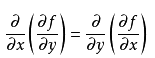相关文章
Hessian矩阵判定极值之MATLAB实现符号解
By WC 1.9 .2015 1.Hessian矩阵 其定义如下: 如果函数f在D区域内二阶连续可导,那么黑塞矩阵H(f) 在 D 内为对称矩阵。原因是:如果函数f连续,则二阶偏导数的求
点云配准之ICP和NDT算法的高斯牛顿法求解
ICP算法 NDT算法 代码:https://github.com/taifyang/pointcloud-registration 参考:高翔《自动驾驶与机器人中的SLAM技术》
【机器人学导论】6自由度机械臂逆运动学求解—牛顿法(数值法,仅旋转关节)
我以前是机器人专业,不过学的不多,教程应该是灰色封面的《机器人学导论》。3年前学的了,软件仿真学的是ABB,上手操作是KUKA的机器人。本文是给别人解决问题的记录,写个笔记。代码是matlab的,不免费分享,但是看我的解析应该也能自己写出来。我不从事这个行业,很多东西已经模糊了。 文章目录 一、DH参数二、正向运动学三、逆向运动学3.1 逆向运动学的求解方法:3.11 解析法(Ana
【高中数学/极值/判别式法】已知实数a和b,b在(0,1)区间,a-b=1,则1/(a-1)+1/(5-4b)的最小值是?
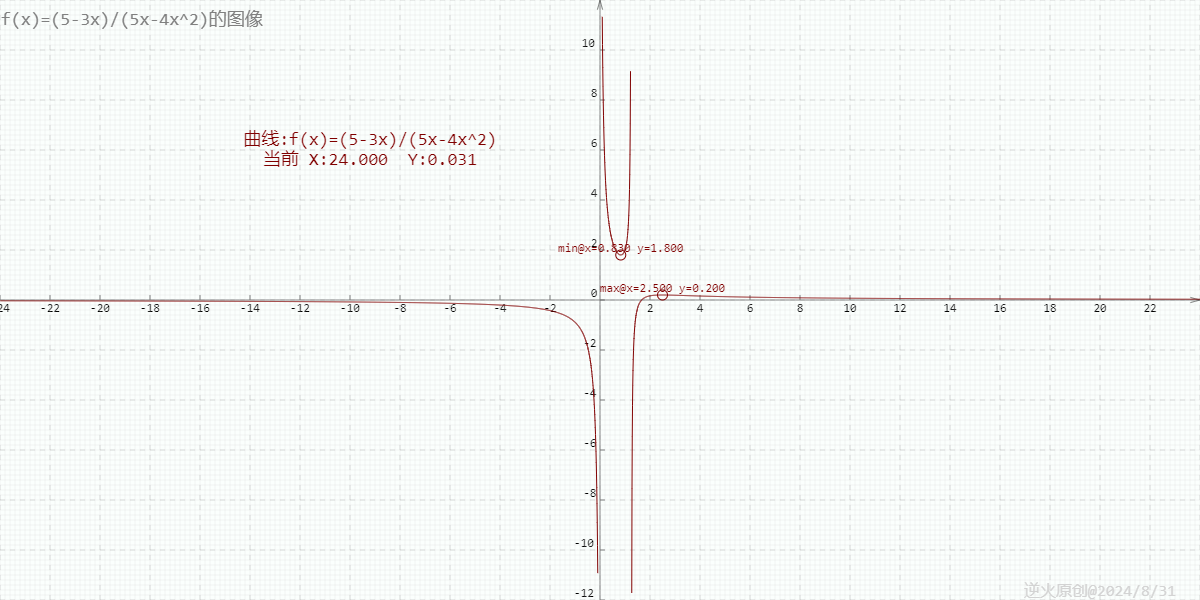
【问题】 已知实数a,b,b在(0,1)区间,a-b=1,则1/(a-1)+1/(5-4b)的最小值是? 【来源】 《解题卡壳怎么办 高中数学解题智慧点剖析》P34 余继光 苏德矿合著 浙江大学出版社出版 【破题点】 将a-1用b取代,发现结果是二次式相除,正好可用判别式法。 【解答】 由a-b=1得到a-1=b 于是原式=1/b+1/(5-4b) 设b为x,结果为y,得到表达式
#1142 : 三分·三分求极值 ( 三分极值 )
#1142 : 三分·三分求极值 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 这一次我们就简单一点了,题目在此: [week40_1.PNG] 在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y),求点P到抛物线的最短距离d。 提示:三分法 输入 第1行:5个整数a,b,c,x,
用数组法求第10亿位斐波那契数列,mod 10000
有人在csdn网上求解一道题目:求第10亿位斐波那契数列,mod 10000,如何才能在1S内得出结果。我试了一下,在一台笔记本上运行30秒内得出答案,1S内得出结果做不到。 程序如下所示: /*20200304, 作者:shencz2000 求第10亿位斐波那契数列,mod 10000 使用mod 10000 运算,一个数万以上的部分被该运算去掉了。 设整数 M 和 N ,M*N = 1
mysql 获取当天零点和当天最后时间
要进行数据统计,统计前一天的数据量 时间处理: 当天零点 SELECT DATE(NOW()) AS today_zero_time; 当天最后时间: SELECT DATE_ADD(ADDDATE(DATE(NOW()), 1), INTERVAL -1 SECOND) AS today_last_time; 昨天零点 SELECT ADDDATE(
5、梯度下降法,牛顿法,高斯-牛顿迭代法
1、梯度下降 2、牛顿法 3、高斯-牛顿迭代法 4、代码部分 1.梯度下降法代码 批量梯度下降法c++代码: /*需要参数为theta:theta0,theta1目标函数:y=theta0*x0+theta1*x1;*/#include <iostream>using namespace std;int main()
数学基础 -- 牛顿法
牛顿法 牛顿法是一种迭代法,用来寻找函数的根(即找到 f ( x ) = 0 f(x) = 0 f(x)=0 的解)。它的基础是泰勒展开,通过利用函数的一阶导数信息,牛顿法能够快速逼近根。 牛顿法的推导 假设我们要找到函数 f ( x ) f(x) f(x) 的根,也就是求解方程 f ( x ) = 0 f(x) = 0 f(x)=0。从一个初始猜测 x 0 x_0 x0 开始,我
07:极限-零点定理和介值定理
1、零点定理 定义:f(x)在[a, b]上连续,且f(a)·f(b) <0.则存在 ξ ∈ \xi ∈ ξ∈[a,b],使 f ( ξ ) = 0 f(\xi)=0 f(ξ)=0 1.1.介值定理(最大最小值定理) 定义:f(x)在[a,b]上连续,则f(x)在[a, b]上有最大值和最小值。即:m≤f(x)≤M。 2介值定理 定义:f(x)在[a,b]上连续,最大值为M,最小值为m,