内在好奇心模型(Intrinsic Curiosity Module,ICM)-论文Curiosity-driven Exploration by Self-supervised Prediction

本文主要是介绍内在好奇心模型(Intrinsic Curiosity Module,ICM)-论文Curiosity-driven Exploration by Self-supervised Prediction，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

关于强化学习的稀疏奖励问题，主要的解决方案有：

1）塑形奖励函数，但是塑形奖励函数一般或多或少的带有设计者的个人主观因素，这可能会导致模型的最优策略发生偏移。目前，防止塑形奖励函数改变最优策略的方法是吴恩达的
Potential-Based Reward Shaping （没了解的可以搜索一下看看，有很多博客）。
2）模仿学习，其实也就是使用专家演示数据引导训练，典型的代表就是DQN中使用的transitions通过专家演示数据生成和使用专家数据预训练DQN的backbone。但是，好用的专家演示数据一般是很难采集的。
3）就是好奇心驱动的探索，也就是本文要分享的方法。.基于好奇心的探索主要分为两类：
第一类是使用预测误差作为内在奖励信号[1][2][3][4][5]，第二类是使用“访问计数[6][7][8][9]”作为内在奖励。

[1] R. Houthooft, X. Chen, Y . Duan, J. Schulman, F. De Turck, and P .Abbeel. Vime: V ariational information maximizing exploration. In NIPS, 2016.
[2] S. Mohamed and D. J. Rezende. V ariational information maximisation for intrinsically motivated reinforcement learning. In NIPS, 2015.
[3] D. Pathak, P . Agrawal, A. A. Efros, and T. Darrell. Curiosity-driven exploration by self-supervised prediction. In ICML, 2017.
[4] J. Schmidhuber. A possibility for implementing curiosity and boredom in model-building neural controllers. In From animals to animats: Proceedings of the first international conference on simulation of adaptive behavior, 1991.
[5] S. P . Singh, A. G. Barto, and N. Chentanez. Intrinsically motivated reinforcement learning. In NIPS, 2005.
[6] M. Bellemare, S. Srinivasan, G. Ostrovski, T. Schaul, D. Saxton, and R. Munos. Unifying count-based exploration and intrinsic motivation. In NIPS, 2016.
[7] M. Lopes, T. Lang, M. Toussaint, and P .-Y . Oudeyer. Exploration in model-based reinforcement learning by empirically estimating learning progress. In NIPS, 2012.
[8] G. Ostrovski, M. G. Bellemare, A. v. d. Oord, and R. Munos. Count-based exploration with neural density models. arXiv:1703.01310, 2017.
[9] P . Poupart, N. Vlassis, J. Hoey, and K. Regan. An analytic solution to discrete bayesian reinforcement learning. In ICML, 2006.

首先看一下这个论文的框架图
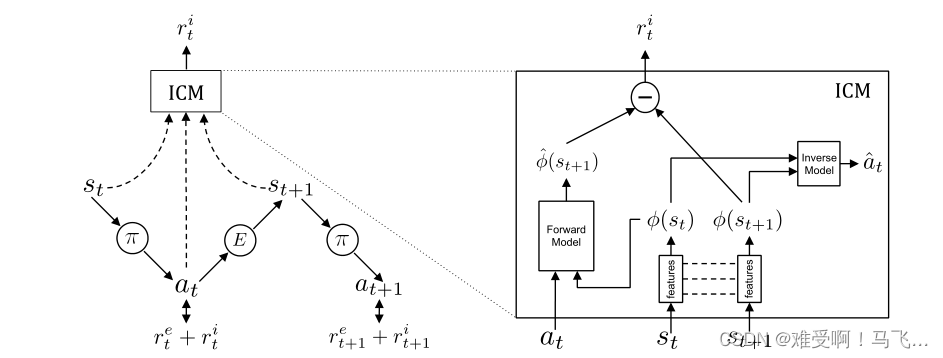
在这里插入图片描述
图 2. 处于状态 $s_{t}$ 的agent通过执行从其当前策略 $π$ 中采样的动作 $a_{t}$ 与环境交互，并最终处于状态 $s_{t+1}$ 。训练策略π以优化环境 E 提供的外在奖励 ( $r_{t}^{e}$ ) 和我们提出的内在好奇心模块 (ICM) 生成的基于好奇心的内在奖励信号 ( $r_{t}^{i}$ ) 的总和。ICM 将状态 $s_{t}$ 、 $s_{t+1}$ 编码为feature $φ(s_{t})$ 、 $φ(s_{t+1})$ ，这些feature经过训练以预测 $a_{t}$ （即逆动力学模型）。前向模型将 $φ(s_{t})$ 和 $a_{t}$ 作为输入，并预测 $s_{t+1}$ 的特征表示。
特征空间中的预测误差被用作基于好奇心的内在奖励信号。

作者的主要意图就是：使用预测误差作为好奇心奖励，这样就是得agent在每一步都可以得到一个奖励了。解决了强化学习面对的稀疏奖励的问题。
因此，这篇文章的核心就是预测误差。下面，我们就解释一下到底是哪些变量的预测误差。

1. 预测两个变量

首先，介绍策略输出网络
这篇论文用参数为 $θ_{P}$ 的深度神经网络表示策略 $π(s_{t}; θ_{P})$ 。给定状态 st的agent，它执行从策略中采样的动作 $a_{t}∼π(s_{t}; θ_{P})$ 。 $θ_{P}$ 被优化以最大化期望的奖励总和，
--------------------------------------- $\min_{\theta_{P}}[\mathbb{E}_{\pi ({s_{t},\theta _{P}})}[\Sigma_{t}r_{t}]]$

------------------------------------------- $r_{t}=r_{t}^{e}+r_{t}^{i}$
--------------------------------- $r_{t}^{i}=\frac{\eta }{2} \left \| \hat{\varphi}(s_{t+1}),φ(s_{t+1}) \right \| _{2}^{2}$

1.1 ICM模块的三个主要结构

从图2可以看出，ICM其实有三个模块，

特征提取器。我们可以将这两个特征提取看做是两个参数相同的深度神经网络，特征提取器输出的 $φ(s_{t})$ 和 $φ(s_{t+1})$ 是特征向量，输入其实就是agent观察到的图像，就是状态 $s_{t}$ 和 $s_{t+1}$ 。
前向模块：forward model。该模块的输入是agent根据当前策略采取的动作 $a_{t}$ 和当前状态的特征向量 $φ(s_{t})$ 。输出是对下一时刻状态的特征向量的预测值 $\hat{\varphi}(s_{t+1})$ 。
逆模块: inverse model。该模块的输入当前状态的特征向量 $φ(s_{t})$ 和下一时刻状态的特征向量 $φ(s_{t+1})$ 。输出是对当前动作的预测值 $\hat{a}_{t}$ 。需要指出的是， $\hat{a}_{t}$ 是通过softmax处理的值。

1.2 逆模型预测动作 $a_{t}$

从上面1.1节的分析可以看出，ICM的第一个预测值是对当前动作的预测值，输入是前后两个状态的特征向量，在这里，我们可以简单的将其看作是多智能体强化学习中的high-level Communication mechanism。这个操作让agent具有“全局观察能力”，其实也可以认为是这个操作让agent在时间上具有更大的视野。
逆模型的损失函数可以表示为：
---------------------------------------- $\min_{\theta_{I},\theta_{E}} L_{I}(\hat{a}_{t},a_{t})$
逆模型的表达式可以表示为：
------------------------------------------- $\hat{a}_{t}=g(\varphi (s_{t}),\varphi (s_{t+1});\theta_{I} )$
其中， $L_{I}$ 衡量了预测动作与实际动作之间的差异。当 $a_{t}$ 是离散的时， $L_{I}$ 被建模为所有可能动作的 softmax 损失。学习到的函数 $g$ 也称为逆动力学模型(inverse dynamics model)，学习 $g$ 所需的元组 ( $s_{t}$ , $a_{t}$ , $s_{t+1}$ ) 是在agent使用其当前策略 $π (s)$ 与环境交互时获得的。

个人观点。从逆模块的损失函数可以看出。这个模块的作用是输出当前动作的预测值 $\hat{a}_{t}$ 。与该模块相关的顺势函数其实就是最小化当前策略输出的动作 $a_{t}$ 与逆模型输出的动作 $\hat{a}_{t}$ 之间的误差。
更信息的分析逆模型的作用，还需要进一步结合整体的损失函数来分析。不要急，我会在1.4节解释。

1.3 前向模块预测状态 $s_{t+1}$

这个模块其实挺有意思的，它输入的是当前的动作 $a_{t}$ 和当前状态的特征向量 $s_{t+1}$ ，输出是下一个状态的特征向量的预测值 $\hat{\varphi}(s_{t+1})$ 。
首先看一下这个模块对应的损失函数：
---------------------------------- $\min_{\theta_{F},\theta_{E}} L_{F}(\hat{\varphi}(s_{t+1}),\varphi(s_{t+1}))$
这个模块的输入输出表达式可以表示为：
------------------------------------------- $\hat{\varphi}(s_{t+1})=f(\varphi (s_{t}),a_{t};\theta_{F} )$
前向模型有助于学习一个特征空间，该特征空间编码的信息仅用于预测agent的动作，而正向模型使这种学习的特征表示更具可预测性。

1.4 总的损失函数

--------------------------------- $\min_{\theta_{P},\theta_{I}，\theta_{F},\theta_{E}}[-\lambda \mathbb{E}_{\pi ({s_{t},\theta _{P}})}[\Sigma_{t}r_{t}]+(1-\beta )L_{I}+\beta L_{F}]$
其中 $0 \leq β \leq 1$ 是一个衡量反向模型损失和正向模型损失的标量， $λ > 0$ 衡量策略梯度损失和内在奖励信号的重要性。我们不将策略梯度损失反向传播到正向模型，以防止agent奖励它自己的退化解。
原文中的这句话很难理解，什么叫“防止agent奖励它自己的退化解”。

综合来看， $L_{F}$ 和 $L_{I}$ ,也就是预测动作和预测状态的前向模型和逆模型对整体损失函数的贡献是互斥的，也就是说他们两个是一个变大，另一个就会变小。

1.5 好奇心奖励 $r_{t}^{i}$

$r_{t}^{i}=\frac{\eta }{2} \left \| \hat{\varphi}(s_{t+1}),φ(s_{t+1}) \right \| _{2}^{2}$
简单的将，好奇心奖励就是 $\hat{\varphi}(s_{t+1})$ 和 $φ(s_{t+1})$ 的二范数，其实就是衡量实际值和预测值之间的误差，误差越大，二范数的值越大，则好奇心奖励的值就越大，那么这就越会鼓励agent去探索。