本文主要是介绍openGL投影矩阵(OpenGL Projection Matrix),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
英文原版地址
前言
先上一个运行效果图:
项目完整代码工程

Overview
A computer monitor is a 2D surface. A 3D scene rendered by OpenGL must be projected onto the computer screen as a 2D image. GL_PROJECTION matrix is used for this projection transformation. First, it transforms all vertex data from the eye coordinates to the clip coordinates. Then, these clip coordinates are also transformed to the normalized device coordinates (NDC) by dividing with w component of the clip coordinates.
翻译:
概述
计算机显示器是一个二维表面。由OpenGL渲染的3D场景必须作为2D图像投影到计算机屏幕上。GL_PROJECTION matrix投影 矩阵 用于此投影 转变。首先,它将所有顶点数据从眼睛坐标(相机坐标系)转换为裁剪坐标系。然后,裁剪坐标系转换到标准设备坐标系(NDC)通过除以裁剪坐标系的w分量。
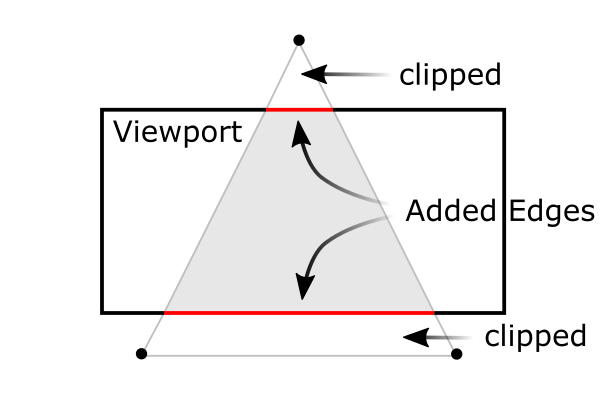
A triangle clipped by frustum
Therefore, we have to keep in mind that both clipping (frustum culling) and NDC transformations are integrated into GL_PROJECTION matrix. The following sections describe how to build the projection matrix from 6 parameters; left, right, bottom, top, near and far boundary values.
Note that the frustum culling (clipping) is performed in the clip coordinates, just before dividing by wc. The clip coordinates, xc, yc and zc are tested by comparing with wc. If any clip coordinate is less than -wc, or greater than wc, then the vertex will be discarded.![]()
Then, OpenGL will reconstruct the edges of the polygon where clipping occurs.
翻译:
因此,我们必须记住:两次裁剪(视锥体裁剪剔除)和标准化设备坐标(NDC)转换是通过GL_PROJECTION matrix.投影矩阵完成。以下章节描述:如何从6个参数:左、右上、下远、近边缘值构建投影矩阵。
请注意:视锥体裁剪剔除是在裁剪坐标系下执行的,是在除以Wc之前。在裁剪坐系下:Xc、Yc和Zc通过和Wc进行比较,如果裁剪坐标小于-Wc或者大于Wc,那么这些顶点将会被丢弃。
-Wc < Xc,Yc,Zc
然后,openGL会建视锥体裁剪剔除多面体的边缘。
Perspective Projection
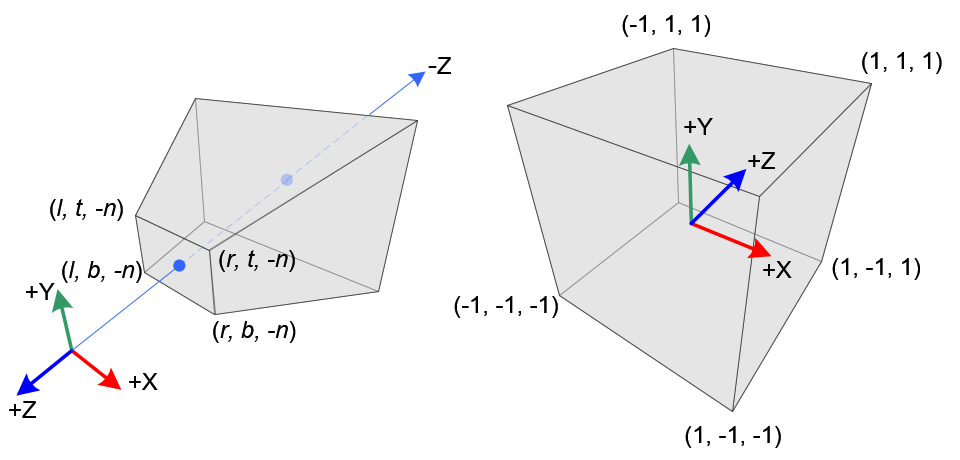
Perspective Frustum and Normalized Device Coordinates (NDC)
In perspective projection, a 3D point in a truncated pyramid frustum (eye coordinates) is mapped to a cube (NDC); the range of x-coordinate from [l, r] to [-1, 1], the y-coordinate from [b, t] to [-1, 1] and the z-coordinate from [-n, -f] to [-1, 1].
Note that the eye coordinates are defined in the right-handed coordinate system, but NDC uses the left-handed coordinate system. That is, the camera at the origin is looking along -Z axis in eye space, but it is looking along +Z axis in NDC. Since glFrustum() accepts only positive values of near and far distances, we need to negate them during the construction of GL_PROJECTION matrix.
In OpenGL, a 3D point in eye space is projected onto the near plane (projection plane). The following diagrams show how a point (xe, ye, ze) in eye space is projected to (xp, yp, zp) on the near plane.
翻译:
视锥体裁剪剔除和标准化设备坐标(NDC)
在透视投影中,一个3D点是在一个截去上半部分的金字塔形状内(视图坐标系)被映射到一个立方体(NDC);x坐标的范围从[l,r]到[-1,1],y坐标的范围从[b,t]到[-1,1],z坐标的范围从[-n,-f]到[-1,1]。
请注意:视图坐标系(相机坐标系或者眼睛坐标系)定义的是右手坐标系,但是NDC(标准设备坐标系)使用的是左手坐标系。也就是说:在视图坐标系下:相机在原点处向负Z轴看去,而在NDC(标准设备坐标系)下沿着正Z轴看去。由于glFrustum()函数只接受参数near和far参数的距离值为正,我们必须在投影矩阵创建期间把near和far取反。
在openGL中,在视图空间中的一个3D点,被投影到近平面(透视面)。下图中一个点(Xe,Ye,Ze)投影到视椎体的近平面(Xp,Yp,Zp)上。
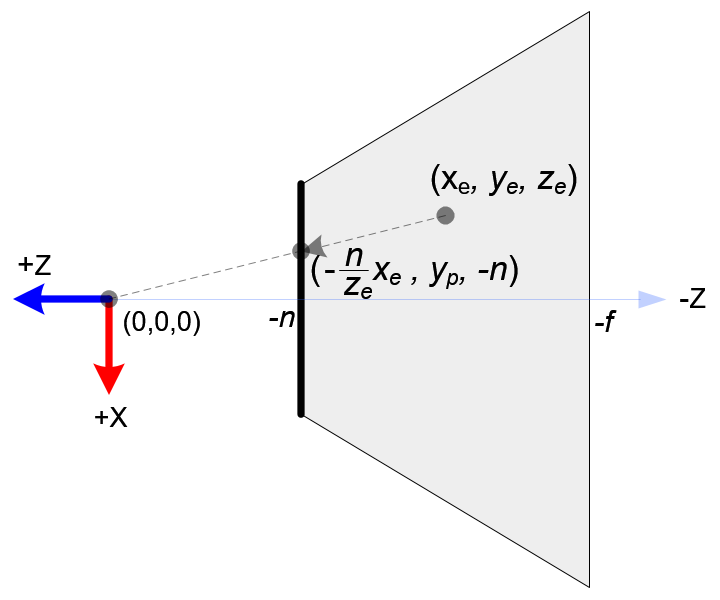
Top View of Frustum
翻译:视椎体的顶视图
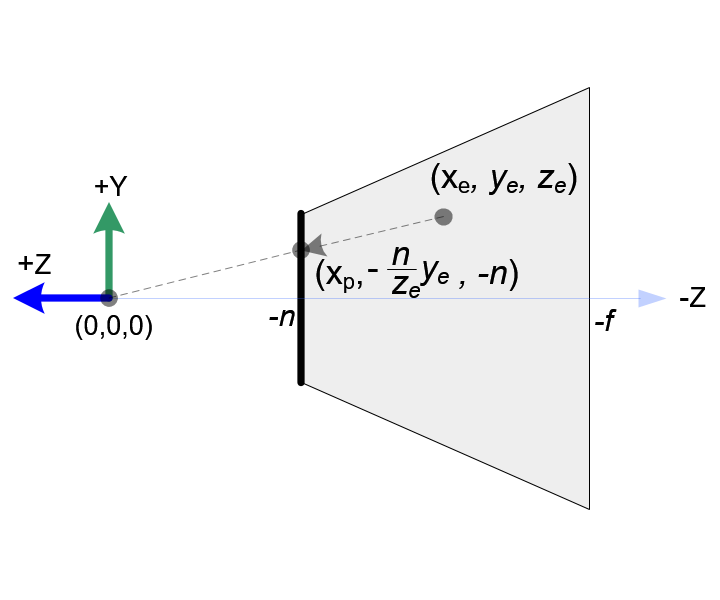
Side View of Frustum
From the top view of the frustum, the x-coordinate of eye space, xe is mapped to xp, which is calculated by using the ratio of similar triangles;
翻译:
从视椎体顶视图看,视图空间的x坐标,利用相似三角形比例计算,Xe被映射到Xp
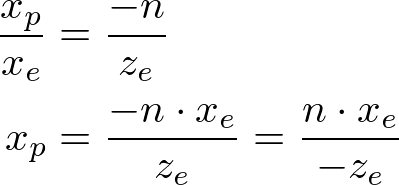
From the side view of the frustum, yp is also calculated in a similar way;
翻译:从视椎体的另一方面,Yp坐标也用同样的方法计算。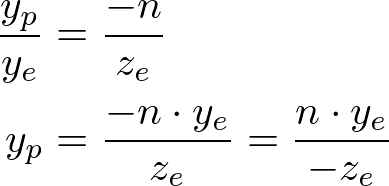
Note that both xp and yp depend on ze; they are inversely propotional to -ze. In other words, they are both divided by -ze. It is a very first clue to construct GL_PROJECTION matrix. After the eye coordinates are transformed by multiplying GL_PROJECTION matrix, the clip coordinates are still a homogeneous coordinates. It finally becomes the normalized device coordinates (NDC) by divided by the w-component of the clip coordinates. (See more details on OpenGL Transformation.)
翻译:
请注意:Xp和Yp依赖Ze;他们和-Ze成反比,换句话说:他们两个除以-Ze,这时构造GL_PROJECTIO矩阵第一条线索,然后视图坐标系通过乘以透视矩阵转换。裁剪坐标依旧是齐次坐标。裁剪坐标除以W分量,最终成为标准设备坐标。
 ,
, 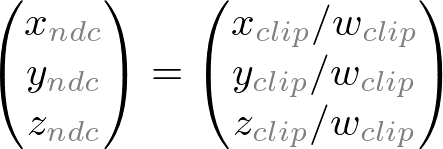
Therefore, we can set the w-component of the clip coordinates as -ze. And, the 4th of GL_PROJECTION matrix becomes (0, 0, -1, 0).
翻译:因此,我们能够将裁剪坐标的w分量设置为-Ze,并且,把投影矩阵第四列变换成(0, 0, -1, 0)。
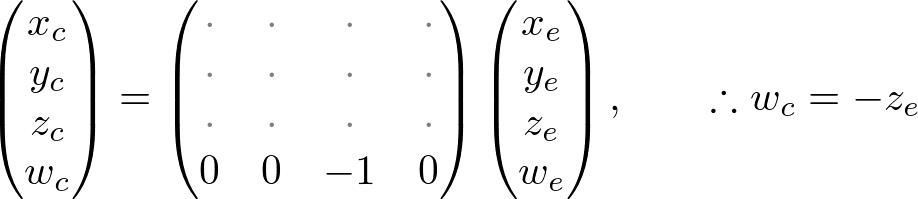
Next, we map xp and yp to xn and yn of NDC with linear relationship; [l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1].
翻译:接下来,我们通过线性关系把投影坐标Xp和Yp转换成NDC下的Xn和Yn,即:[l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1].
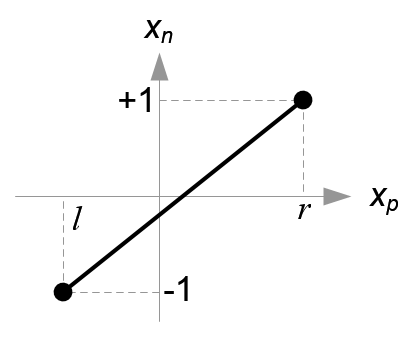
Mapping from xp to xn
翻译:从Xp映射成Xn
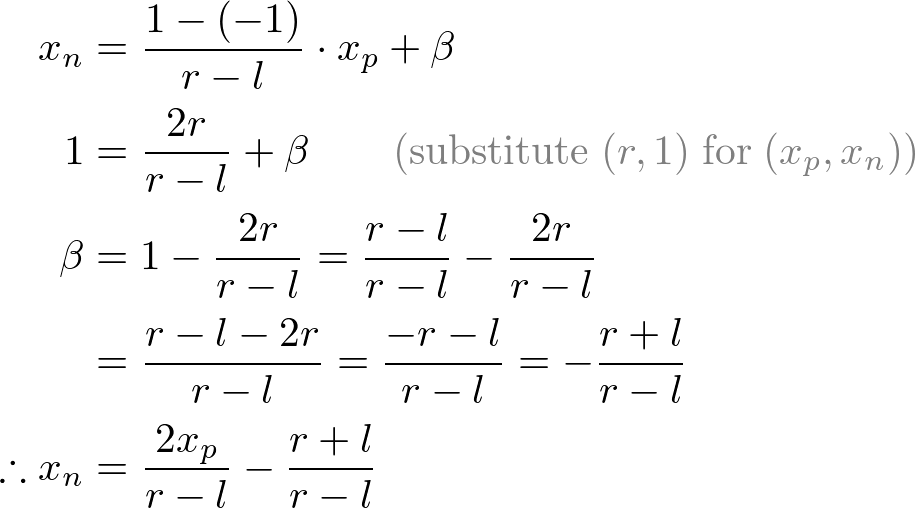
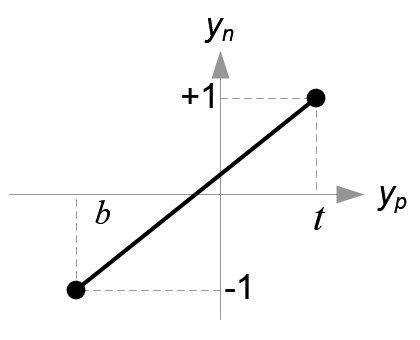
Mapping from yp to yn
翻译:从Yp映射成Yn
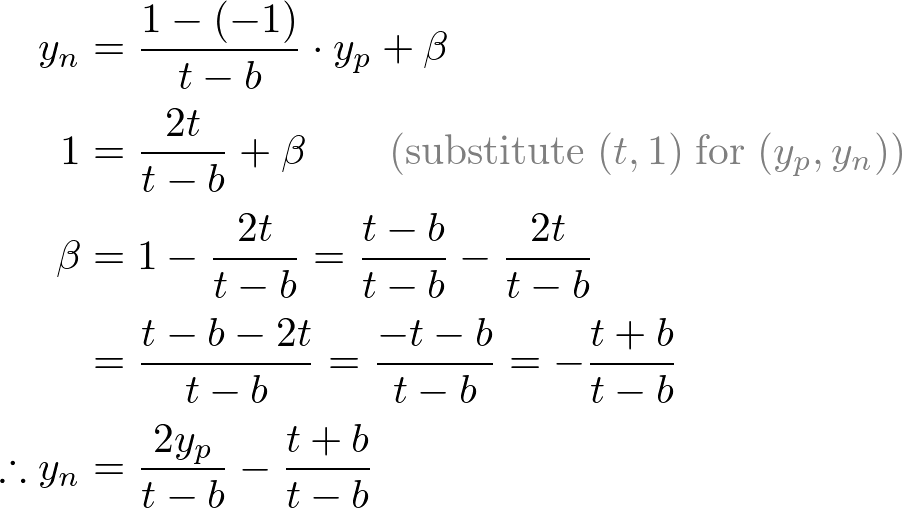
Then, we substitute xp and yp into the above equations.
翻译:然后,我们替换Xp和Yp代入上面的方程。
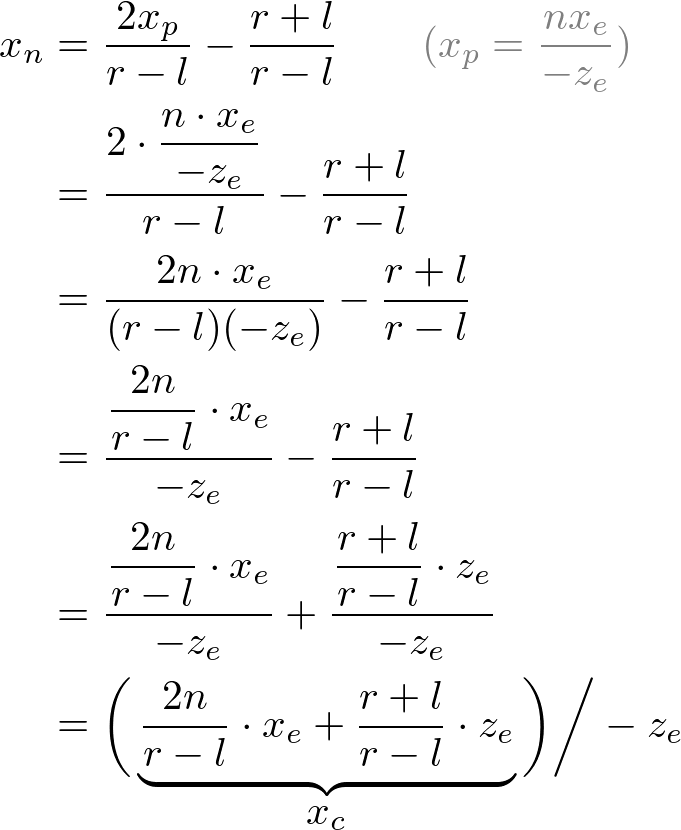
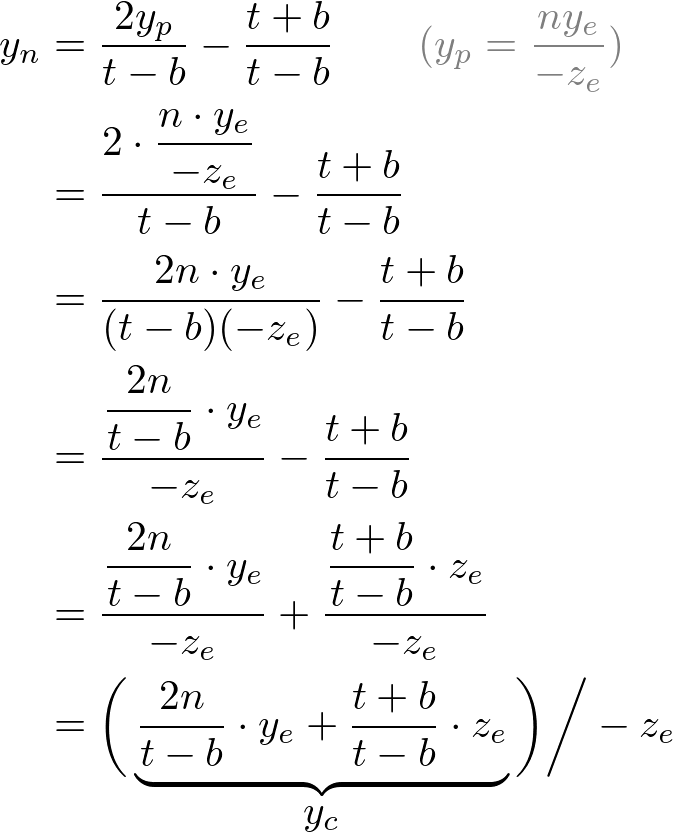
Note that we make both terms of each equation divisible by -ze for perspective division (xc/wc, yc/wc). And we set wc to -ze earlier, and the terms inside parentheses become xc and yc of the clip coordiantes.
From these equations, we can find the 1st and 2nd rows of GL_PROJECTION matrix.
翻译:
请注意:我们使两个方程都除以-Ze,(Xc/Wc,Yc/Wc),并且,我们更早设置Wc到-Ze,Xn和Yn方程括号内Xc和Yc是裁剪坐标。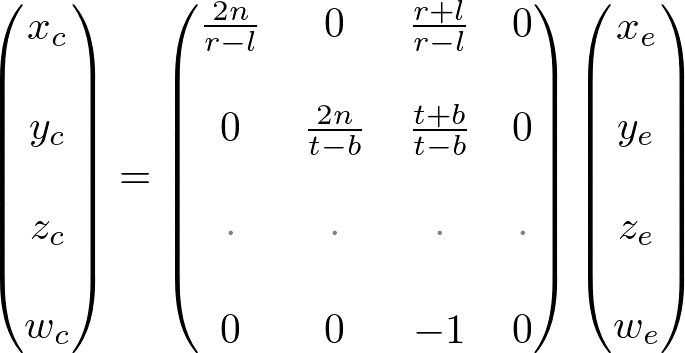
Now, we only have the 3rd row of GL_PROJECTION matrix to solve. Finding zn is a little different from others because ze in eye space is always projected to -n on the near plane. But we need unique z value for the clipping and depth test. Plus, we should be able to unproject (inverse transform) it. Since we know z does not depend on x or y value, we borrow w-component to find the relationship between zn and ze. Therefore, we can specify the 3rd row of GL_PROJECTION matrix like this.
翻译
现在,我们只需要处理投影矩阵的前三行。找到Zn和Xn、Yn有一点不同,因为在视图坐标中总是投影到-n的近平面。我们需要为唯一的z值做裁剪和深度测试,另外,我们应该能够对他取消投影(逆变换)。因此,我们知道Z值不依赖x和y值,所以,我们借用w分量去寻找Zn和Ze之间的关系。因此,我们能像下面指定投影矩阵的前三列。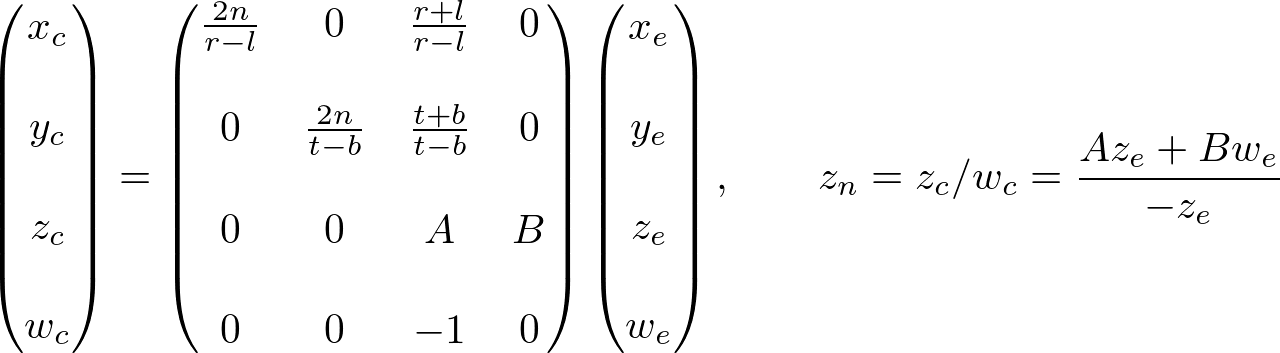
In eye space, we equals to 1. Therefore, the equation becomes;
翻译:
在视图空间中,我们等于1,因此,方程变为:![]()
To find the coefficients, A and B, we use the (ze, zn) relation; (-n, -1) and (-f, 1), and put them into the above equation.
翻译:
为了找到系数, A 和 B、 我们使用(ze,zn)关系(-n、 -1)和(-f,1),并将它们放入上述方程中。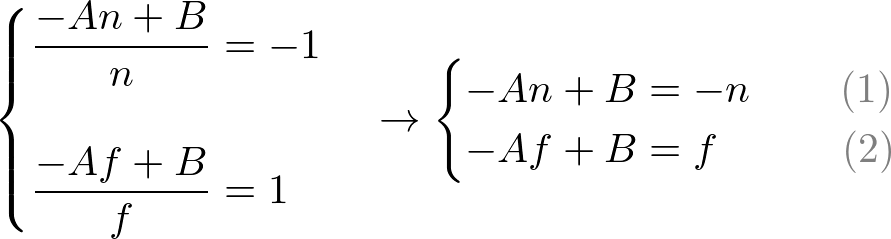
To solve the equations for A and B, rewrite eq.(1) for B;
翻译:
解方程 A 和 B、 为B重写式(1);![]()
Substitute eq.(1') to B in eq.(2), then solve for A;
翻译:
将公式(1’)替换为 B 在式(2)中,求A;
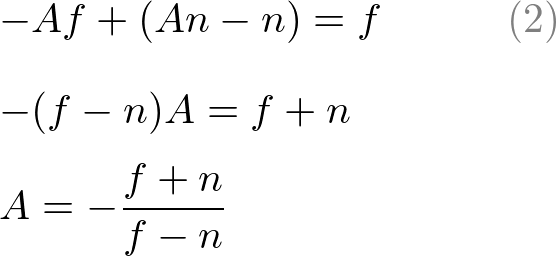
Put A into eq.(1) to find B;
翻译:
放 A 进入式(1)中,找到 B;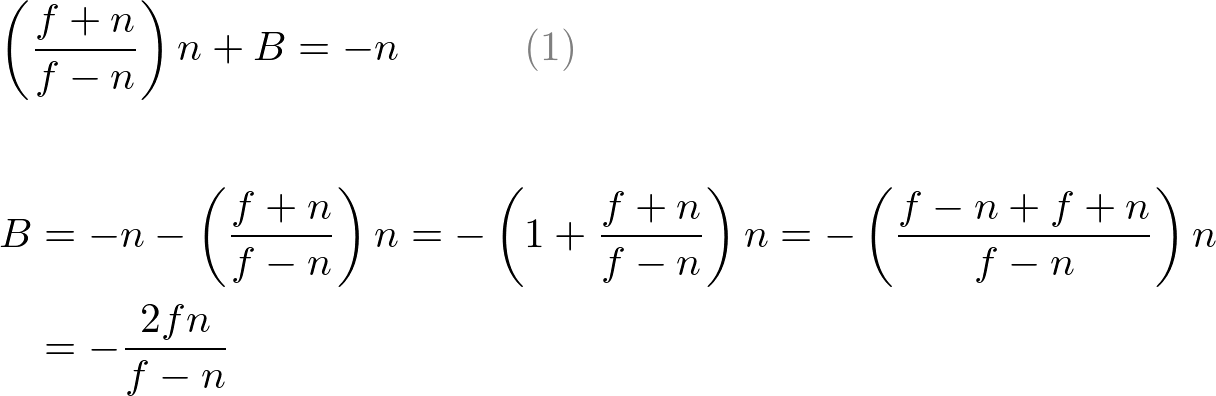
We found A and B. Therefore, the relation between ze and zn becomes;
翻译:
我们发现 A 和 B.因此,ze 变成;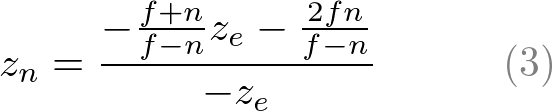
Finally, we found all entries of GL_PROJECTION matrix. The complete projection matrix is;
翻译:
最后,我们找到了投影矩阵的所有值。完成投影矩阵: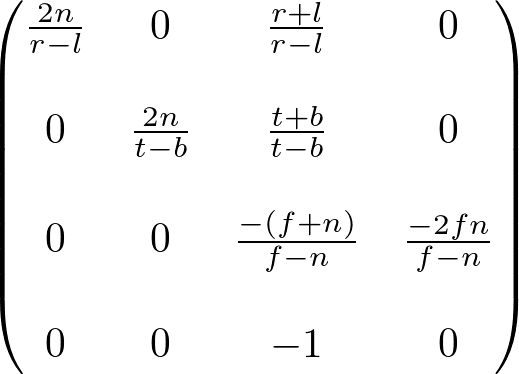
OpenGL Perspective Projection Matrix
翻译:
openGL透视投影矩阵
This projection matrix is for a general frustum. If the viewing volume is symmetric, which is ![]() and
and ![]() , then it can be simplified as;
, then it can be simplified as;
翻译:
这个投影矩阵为一般的视锥体裁,如果我们观察到他的体积是对称的,可以简化为: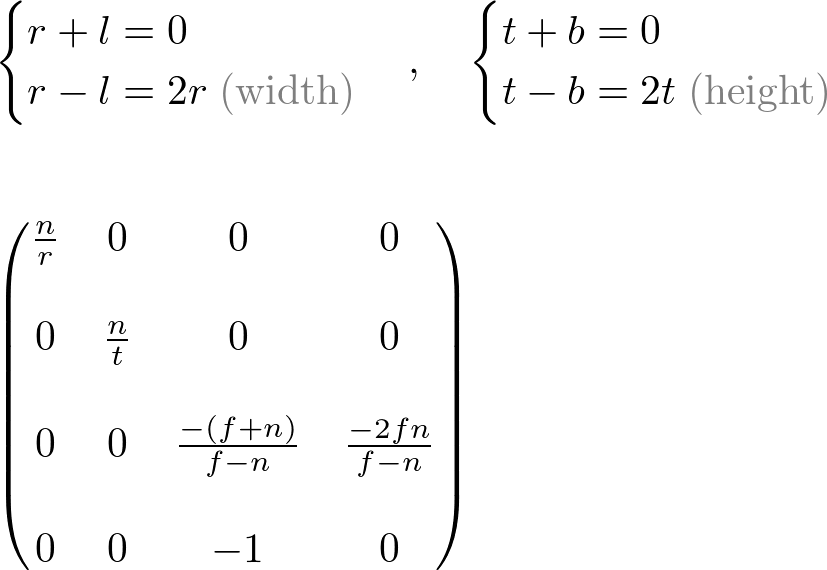
Before we move on, please take a look at the relation between ze and zn, eq.(3) once again. You notice it is a rational function and is non-linear relationship between ze and zn. It means there is very high precision at the near plane, but very little precision at the far plane. If the range [-n, -f] is getting larger, it causes a depth precision problem (z-fighting); a small change of ze around the far plane does not affect on zn value. The distance between n and f should be short as possible to minimize the depth buffer precision problem.
翻译:
在我们继续讨论之前,请先再看看式(3)中,Ze和 Zn之间的关系,。你注意到它是一个有理函数,并且Ze和Zn是非线性关系。这意味着有非常高的精度近平面,但远平面精度很低 。如果范围[-n,-f]越来越大,则会导致深度精度问题(z-fighting);对远平面做一点小的改变对Zn的值没有影响。n和f之间的距离 n 和 f 应尽可能短,以尽量减少深度缓冲精度的问题。
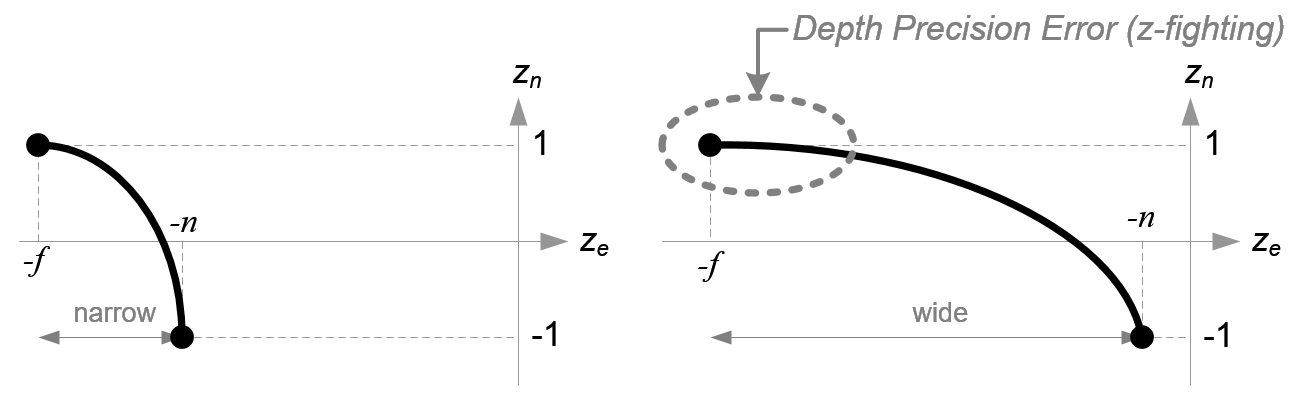
Comparison of Depth Buffer Precisions
翻译:
深度缓冲精度比较
Orthographic Projection
翻译:
正交投影
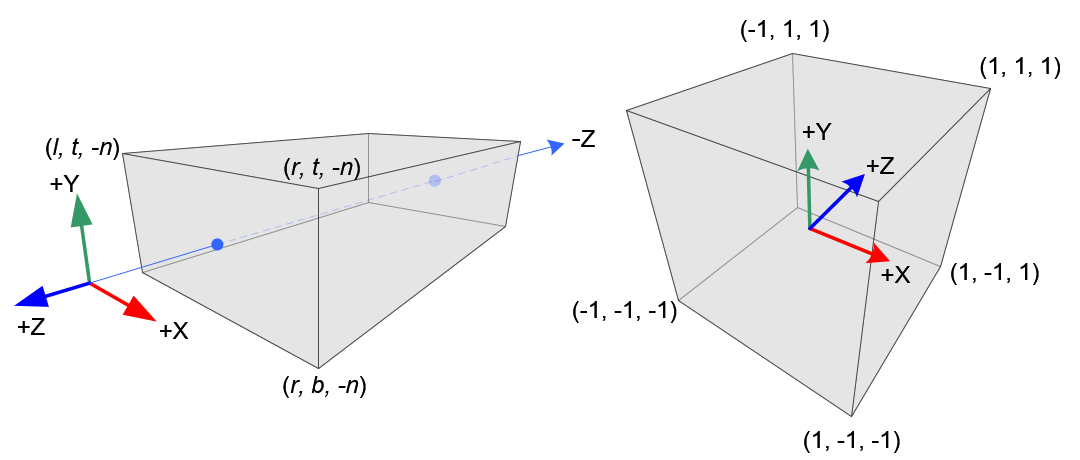
Orthographic Volume and Normalized Device Coordinates (NDC)
Constructing GL_PROJECTION matrix for orthographic projection is much simpler than perspective mode.
All xe, ye and ze components in eye space are linearly mapped to NDC. We just need to scale a rectangular volume to a cube, then move it to the origin. Let's find out the elements of GL_PROJECTION using linear relationship.
翻译
正交体积和标准化设备坐标(NDC)
为正交投影构造投影矩阵比透视模式简单得多。
Xe,Ye和Ze在视图空间中的成分被线性映射到NDC。我们只需要将一个矩形体积缩放成一个立方体,然后将它移到原点。让我们用线性关系找出投影的元素。
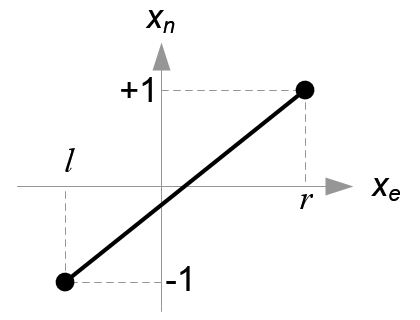
Mapping from xe to xn
翻译:
从Xe到Xn的映射
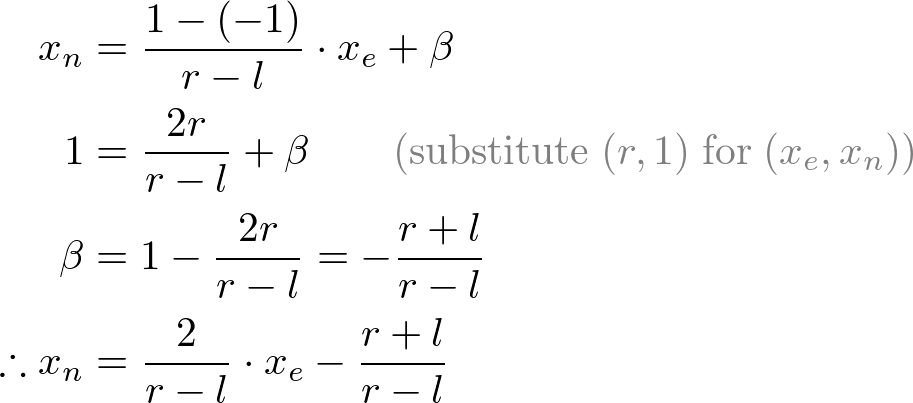
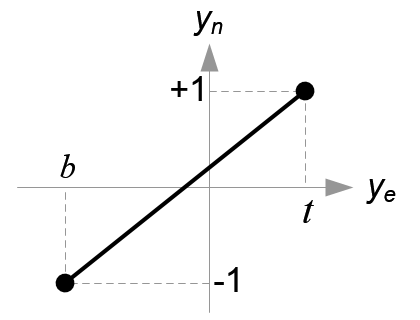
Mapping from ye to yn
翻译:
从Ye到Yn的映射
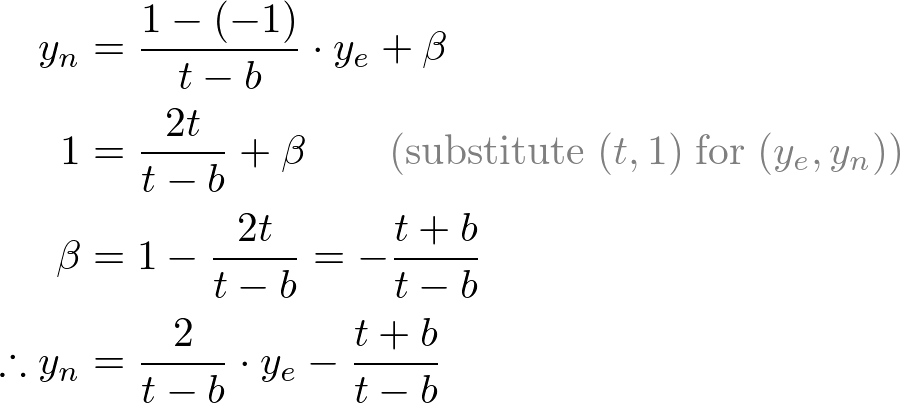
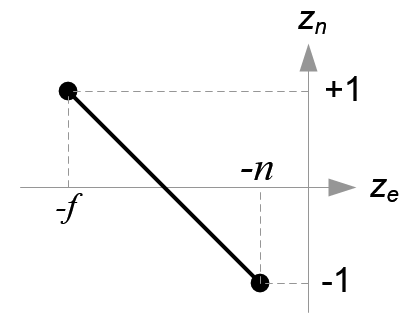
Mapping from ze to zn
从Ze到Zn的映射
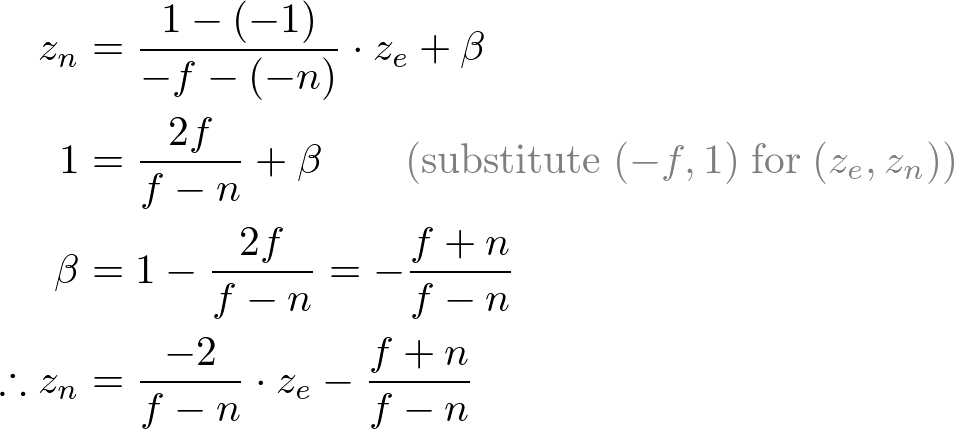
Since w-component is not necessary for orthographic projection, the 4th row of GL_PROJECTION matrix remains as (0, 0, 0, 1). Therefore, the complete GL_PROJECTION matrix for orthographic projection is;
翻译:
由于正交投影不需要w分量,因此投影矩阵的第4行仍然是(0,0,0,1)。因此,完整的投影 矩阵对于正投影是;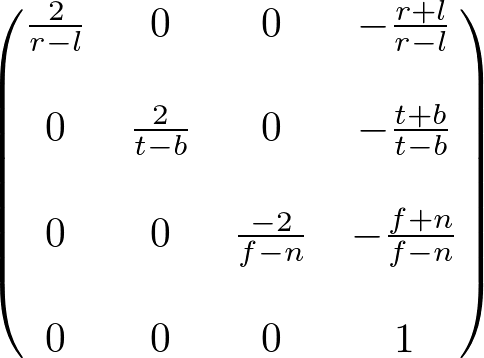
OpenGL Orthographic Projection Matrix
It can be further simplified if the viewing volume is symmetrical, ![]() and
and ![]() .
.
翻译:
OpenGL正交投影矩阵
如果观察体积是对称的,可以进一步简化
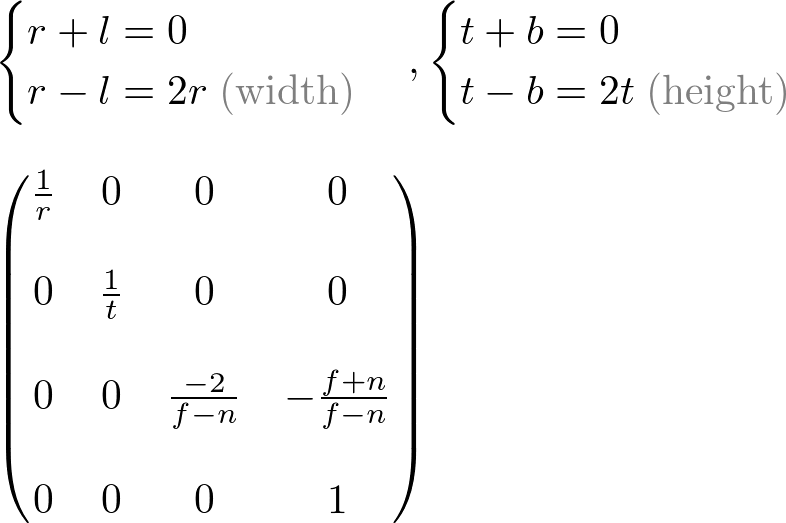
这篇关于openGL投影矩阵(OpenGL Projection Matrix)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)



