matrix专题
![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)
[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale
引言 今天带来第一篇量化论文LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale笔记。 为了简单，下文中以翻译的口吻记录，比如替换"作者"为"我们"。 大语言模型已被广泛采用，但推理时需要大量的GPU内存。我们开发了一种Int8矩阵乘法的过程，用于Transformer中的前馈和注意力投影层，这可以将推理所需
73. Set Matrix Zeros
题目： 解答： 提供了两种解题思路： 第一种，使用两个数组，分别标记每一行、每一列是否有0的存在，然后再去更新二维数组。 第二种，使用两个变量brow，bcol分别标记第0行，第0列是否存在0，然后使用每一行、每一列的第一个单元存储是否该行、该列存在0. 代码： class Solution {public:// 方法一void setZeroes(vector<vector<i
Error: label vector and instance matrix must be double的解决方法
在使用uci下载的数据时，建模时出现这个错误的解决方法 首先现在UCI上面下载数据 然后右键另存为就行了。这样我们就从UCI里面下载到了训练数据 在matlab 点 导入数据，数据类型要记得选第二个， 如果选择最后一个table就会出现这个问题 最后附上代码 %%之前先import wine.date IMPORTED DATA 设为Numeric Matrix (数值矩
python 实现matrix exponentiation矩阵求幂算法
matrix exponentiation矩阵求幂算法介绍 矩阵求幂算法（Matrix Exponentiation）是一种通过利用矩阵乘法的结合律来高效地计算矩阵的幂的算法。这种方法特别适用于在算法竞赛和计算机科学领域中解决需要快速计算矩阵幂的问题，如求解线性递推关系、图论中的路径计数等。 基本思想 矩阵求幂算法的基本思想类似于整数快速幂算法（快速幂算法），通过递归或迭代的方式将矩阵幂的计
![[LeetCode] 240. Search a 2D Matrix II](/front/images/it_default.jpg)
[LeetCode] 240. Search a 2D Matrix II
题：https://leetcode.com/problems/search-a-2d-matrix-ii/description/ 题目 Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties: Integers i
[LeetCode] 566. Reshape the Matrix
题：https://leetcode.com/problems/reshape-the-matrix/description/ 题目 In MATLAB, there is a very useful function called ‘reshape’, which can reshape a matrix into a new one with different size but keep
UVa 11992 Fast Matrix Operations 线段树
UVa 11992 Fast Matrix Operations 题目大意：有一个r行c列的全0矩阵，支持三种操作： 1 x1 y1 x2 y2 v 子矩阵(x1，y1，x2，y2)的所有元素增加v（v > 0）。 2 x1 y1 x2 y2 v 子矩阵(x1，y1，x2，y2)的所有元素设为v（v > 0）。 3 x1 y1 x2 y2 查询子矩阵(x1，y1，x2，y2
【HDU】4965 Fast Matrix Calculation 矩阵快速幂
传送门：【HDU】4965 Fast Matrix Calculation 题目分析：因为比赛的时候写的太匆忙。。写的不堪入目，所以赛后重写了一次，顺便就贴一下了。 因为A*B=C，所以C^(N*N-1) = A*B*A*B*A*...*B*A*B，因为满足结合律所以变成A*( (B*A)^(N*N-2) )*B，因为中间得到的矩阵最大不超过K(K<=6)，所以可以对中间的矩阵快速幂，然
Matrix：重塑APM领域，以简驭繁的性能监控新纪元
在数字化转型的浪潮中，应用程序的性能监控（APM）已成为企业IT架构中不可或缺的一环。随着业务复杂度的提升和用户对体验要求的日益增高，如何高效、精准地监控并优化应用性能，成为了每个开发者和技术团队面临的重大挑战。正是在这样的背景下，腾讯微信团队推出的Matrix APM系统，以其独特的设计理念和强大的功能特性，为APM领域带来了一股清新的风。 1、Matrix：轻量级与高度可
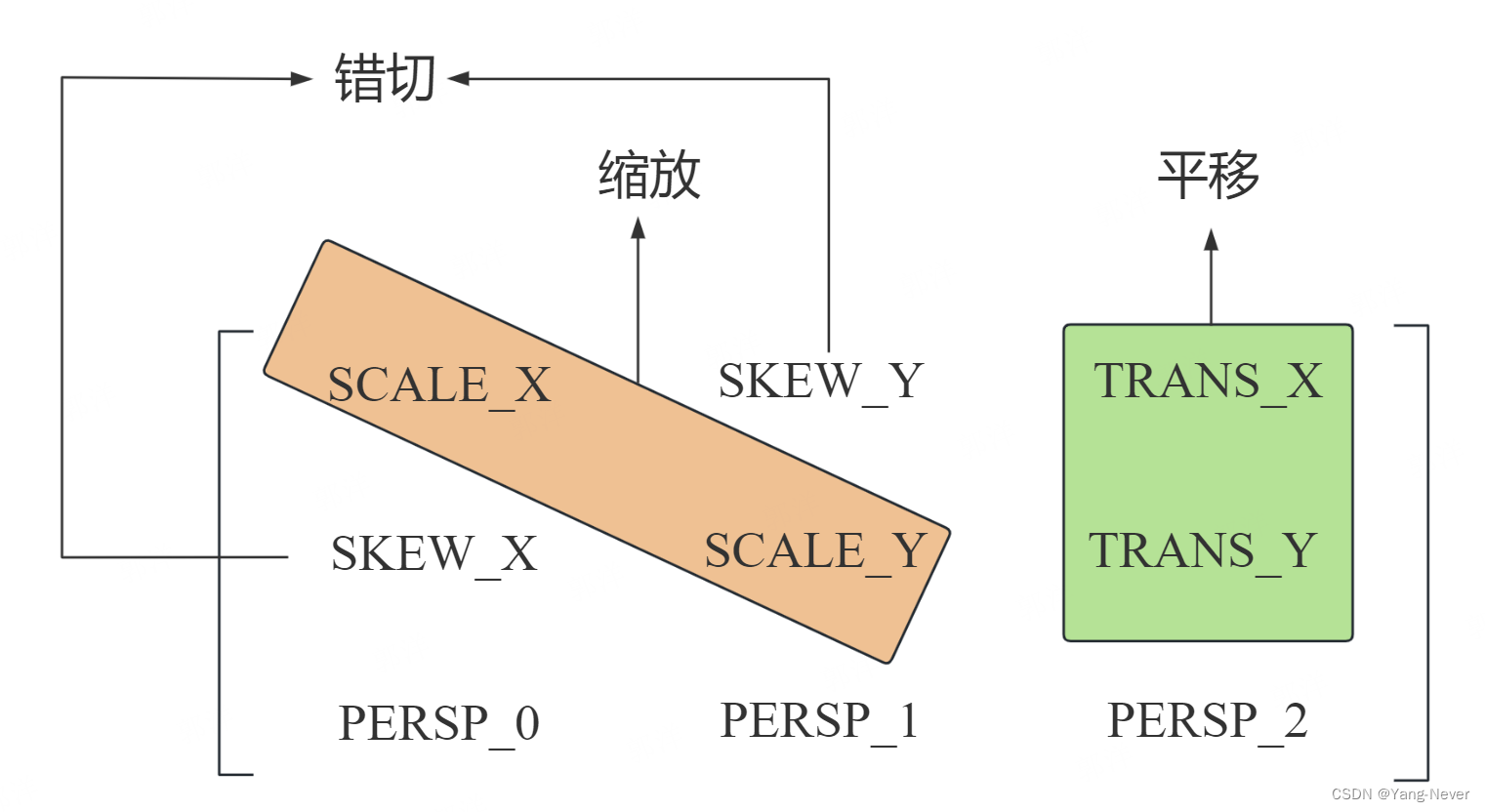
自定义控件（11）---Canvas的平移、旋转、缩放、错切、Matrix直接变换Canvas
Canvas中的变换操作，说起变换，无非就几种：平移、旋转、缩放和错切，而我们的Canvas也继承了变换的精髓，同样提供了这几种相应的方法，前面的很多章节我们也都用到了，像translate(float dx, float dy)方法平移画布用了无数次，这里再次强调，translate方法会改变画布的原点坐标，原点坐标对变换的影响弥足轻重，前面也多次强调了！scale(float sx, floa
Android 画布canvas drawBitmap(Bitmap bitmap, Matrix matrix, Paint paint)
void drawBitmap(Bitmap bitmap, Matrix matrix, Paint paint) Draw the bitmap using the specified matrix. 使用指定的矩阵绘制位图。也就是可以通过matrix的属性来控制如何绘制位图。该方法有三个参数，分别是： Bitmap bitmap：要绘制的位图 Matrix matrix：绘制位图
Android 画布canvas concat(Matrix matrix)
void concat(Matrix matrix) Preconcat the current matrix with the specified matrix. 可以理解成对matrix的变换应用到canvas上的所有对象。 参数Matrix是The Matrix class holds a 3x3 matrix for transforming coordinates.意思。可以理
浅谈android中图片处理之图形变换特效Matrix(四)
今天，我们就来谈下android中图片的变形的特效，在上讲博客中我们谈到android中图片中的色彩特效来实现的。改变它的颜色主要通过ColorMatrix类来实现。 现在今天所讲的图片变形的特效主要就是通过Matrix类来实现，我们通过上篇博客知道，改变色彩特效，主要是通过ColorMatrxi矩阵的系数，以及每个像素点上所对应的颜色偏移量。而今天的图形变换与那个也是非常的类似。它是一个３＊
uva11082 Matrix Decompressing 最大流
题意：已知一个n*m的矩阵每行没列之和，得出一个满足条件的矩阵。 分析：建一个二分图，每一行对应一个X节点，每一列对应一个Y节点，增加一个源点s，s到X节点容量为对应行的和，Y到汇点t的容量为对应列的和，Xi到Yj的容量为19.由于任意元素[1,20]，为了用容量表示值，所有元素减1，就变成[0,19]，所以把容量上限设为19； #include<iostream>#include<st
hdu5226 Tom and matrix 公式，Lucas
题意：给定x1,y1,x2,y2,求和C(i,j)，(x1<=i<=x2,y1<=j<=y2)，结果%p。 分析：因为\sum_{i=a}^{b}C_{i}^{k}=C_{b+1}^{k+1}-C_{a}^{k+1}∑i=abCik=Cb+1k+1−Cak+1 所以求同一列的数的和可以变成求两个组合数的差。由于p可能很小，当除数为p的倍数时就为0了，直接乘逆元会出
从行或列的角度思考矩阵-向量乘法（matrix-vector multiplication）
从行或列的角度思考矩阵-向量乘法可以帮助理解这个运算的几何意义以及如何在计算中操作。 1. 从行的角度思考 假设我们有一个 m × n m \times n m×n的矩阵 A A A 和一个 n × 1 n \times 1 n×1的列向量 x \mathbf{x} x。矩阵-向量乘法 A x A\mathbf{x} Ax 的结果是一个 m × 1 m \times 1 m×1的列
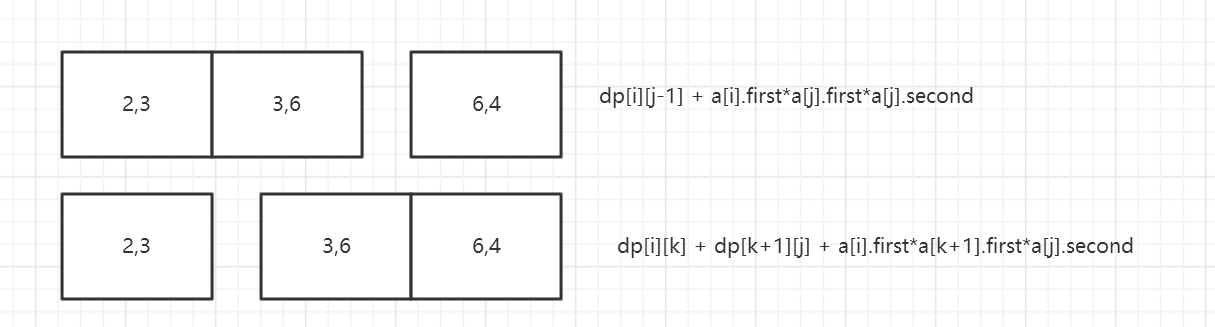
Matrix Chain Multiple
矩阵链乘 题意： 给定多个矩阵，相邻两个矩阵两两之间可以互乘。给出一个乘法的次序使得总的计算量最小。 例： [2,3] [3,6] [6,4] [4,5] 我们可以使用括号表示先后顺序 ((01)(23)) 所以乘法的次数为： 2*3*6 +6*4*5 + 2*6*5 = 36 + 120 + 60 = 216 显然这样不是最优的，我们可以找出另一种乘法的方法 (((01)2)
poj3318--Matrix Multiplication（随机算法）
题目链接：点击打开链接 题目大意：给出三个n*n矩阵的矩阵a，b，c问a*b是否等于c，等于输出YES，否则输出NO n的最大值是500，计算矩阵乘法的话需要O(n^3)的复杂度，很明显超时。 随机出一列k，计算a*(b*k) 和c*k，计算出一列的值，这样的如果a*b==c那么a*(b*k) 和c*k也一定会相等的，因为是随机的数，所以可以多测试几次。 #include <cstdi
POJ 2155 Matrix (二维树状数组)
题意：给一个N*N的零一矩阵，每个操作询问某点的值或者翻转一个矩形区间。 思路：转换题目，新建A矩阵，A矩阵中每一点的值表示，以这一点为左下角的特殊矩形被翻转的次数， 然后用容斥原理把翻转一个矩形表示成翻转四个特殊矩形（以矩阵右边界和矩阵上边界为边界的矩形）， 翻转矩形，就只需要把四个点的A矩阵值+1. 然后一个点的状态就要记录这个点被翻了多少次，也就是这个点左下角中的A矩阵值之和。
Reshape the Matrix问题及解法
问题描述： In MATLAB, there is a very useful function called 'reshape', which can reshape a matrix into a new one with different size but keep its original data. You're given a matrix represented by a
POJ 3233 Matrix Power Series 矩阵快速幂求A+A2+A3+…+Ak
题意 ：给出n k m 和一个n*n的矩阵A 求A + A2 +A3 + … + Ak 参考http://blog.csdn.net/wangjian8006/article/details/7868864 构造矩阵很重要啊！！！ 弱菜不会啊 #include <cstdio>#include <cstring>const int mod = 10000;const int maxn
Matrix-＞Matrix工具类获取Matrix的平移、缩放、错切数值
// 传入矩阵，获取矩阵数值class MatrixValues(matrix: Matrix) {val scaleX: Floatval scaleY: Floatval transX: Floatval transY: Floatval skewX : Float val skewY : Floatinit {val fromValues = FloatArray(9)matrix.g
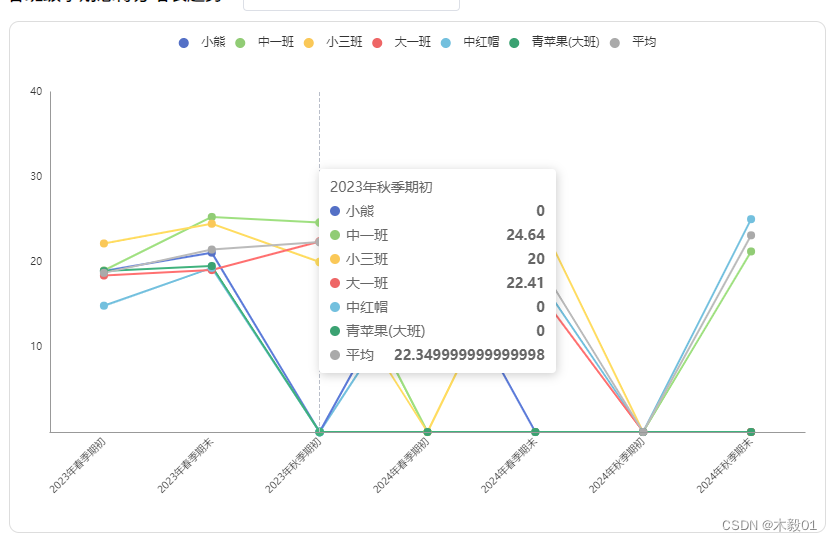
js算法 计算每一列的平均值 求matrix数组对应列的平均值 组成一个新的数组 matrix数组有6行 如果某一行里的值是0则不纳入平均的分母里
let matrix = [[18.95, 21.1, 0, 23, 0, 0, 0],[19, 25.3, 24.64, 0, 0, 0, 21.24],[22.18, 24.5, 20, 0, 26, 0, 0],[18.41, 19.05, 22.41, 27.67, 17, 0, 0],[14.86, 19.31, 0, 19.4, 18.71, 0, 25.04],[18.93, 19.
稀疏矩阵coo_matrix、csr_matrix
coo_matrix 内存占用比csr_matrix少，易手工构建 例如： data即元素，row,col分别是稀疏矩阵中元素的坐标位置 >>> import numpy as np>>> data = np.array([4,5,7,9])>>> dataarray([4, 5, 7, 9])>>> row = np.array([0,3,1,0])>>> rowarray([0