Matrix Chain Multiple

本文主要是介绍Matrix Chain Multiple，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

矩阵链乘
题意：
给定多个矩阵，相邻两个矩阵两两之间可以互乘。给出一个乘法的次序使得总的计算量最小。
例：
[2,3] [3,6] [6,4] [4,5]

我们可以使用括号表示先后顺序
((01)(23))
所以乘法的次数为：
2*3*6 +6*4*5 + 2*6*5 = 36 + 120 + 60 = 216
显然这样不是最优的，我们可以找出另一种乘法的方法
(((01)2)3)
2*3*6 + 2*6*4 + 2*4*5 = 36+48+40 = 124

给出一个具备乘法性质的n个矩阵【A[i].second == A[i+1].first】
问最小的乘法运算次数是多少。

---

这道题算是自己一点点推出来的。
首先通过样例我们可以联想到构建一个二维DP数组，使得dp[i][j]为i~j区间内相乘的最小数量。
我们知道单个矩阵是不需要做乘法所以dp[i][i]=0;
而i~j区间有可能经过拆分之后，获取到更小的值，所以我们令k且k>=i && k< j .
得到dp方程
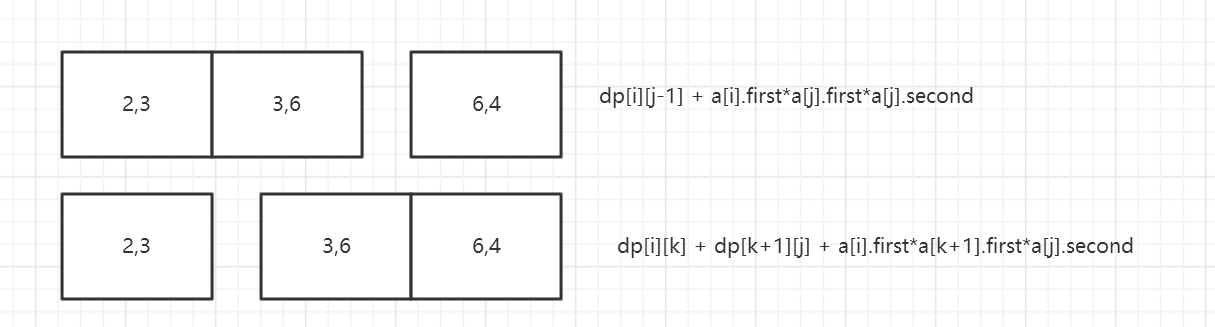
dp[i][j]=min{

• dp[i][j-1] + a[i].first*a[j].first*a[j].second
• dp[i][k]+dp[k+1][j] + a[i].first * a[k+1].first*a[j].last k>i && k< j
  //update: 08-17 10:28
• 两个其实可以被合并到一种情况的,因为第一种情况实际上是下面一种情况在k==j-1的情况下的特例
  }

也即下图

由于我们在推i~j的时候，可能会用到k+1~j而k+1显然是大于i的。
所以我们需要从后往前推。
这样才能保证求i~j的时候，i~k 和 k+1~j已经全部求出。

#include<stdio.h> 
#include<stdlib.h>
#include<string.h>
#include<vector>
#include<limits> 
#include<ctype.h>
#include<algorithm>
#define N 200
using namespace std;int dp[N][N];class Solution{
public:void getMinMatrixMulti(vector<pair<int,int> > &chain){int n=chain.size();//从后往前推 for(int i=n-1;i>=0;i--) {for(int j=i+1;j<n;j++){int min=INT_MAX;
//              for(int k=i+1;k<j;k++){
//                  if(dp[i][k]+dp[k+1][j]+chain[i].first*chain[k+1].first*chain[j].second<min)
//                  min=dp[i][k]+dp[k+1][j]+chain[i].first*chain[k+1].first*chain[j].second;
//              }
//              if(min> dp[i][j-1]+chain[i].first*chain[j].first*chain[j].second)
//              min = dp[i][j-1]+chain[i].first*chain[j].first*chain[j].second;for(int k=i;k<j;k++){if(dp[i][k]+dp[k+1][j]+chain[i].first*chain[k+1].first*chain[j].second<min)min=dp[i][k]+dp[k+1][j]+chain[i].first*chain[k+1].first*chain[j].second;}dp[i][j]=min;}}}
};int main(){vector<pair<int,int> > chain;chain.push_back(make_pair(2,3));chain.push_back(make_pair(3,6));chain.push_back(make_pair(6,4));chain.push_back(make_pair(4,5));memset(dp,0,sizeof(dp));Solution solution;solution.getMinMatrixMulti(chain);for(int i=0;i<chain.size();i++){for(int j=0;j<chain.size();j++){printf("%d ",dp[i][j]);}printf("\n");}printf("\n");printf("%d\n",dp[0][chain.size()-1]);system("pause");return 0;
}

这篇关于Matrix Chain Multiple的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---