本文主要是介绍[C语言][C++][时间复杂度详解分析]二分查找——杨氏矩阵查找数字详解!!!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一,题目
遇到的一道算法题:
1,已知有一个数字矩阵(row行,col列),矩阵的每行 从左到右 递增,每列 从上到下 递增。
2,现输入一个数字 num ,判断数字矩阵中是否存在该元素,若存在,求出此数字在矩阵的哪一行,哪一列?(求出其中一组行列即可)
3,要求:时间复杂度小于O(N)。
二,简介杨氏矩阵
此题目中的矩阵也叫做杨氏矩阵,通常可以用二维数组来表示。
杨氏矩阵画图举例:

解决此题并不需要深刻理解杨氏矩阵。
但若有需要,杨氏矩阵详解链接附上:杨氏矩阵 - OI Wiki (oi-wiki.org)
三,各种解法(时间复杂度的详解)以及思考
3.1:暴力遍历
3.1.1:详解代码
for (int i = 0; i < row; i++)
{for (int j = 0; j < col; j++){if (Y_arr[i][j] == search){printf("%d %d\n", i, j);}}
}3.1.2:时间复杂度分析
最坏的情况下,此方法的时间复杂度为 O(rwo * col)。
不符合题目要求。
优化!
3.2:对每行元素进行二分查找
3.2.1:在代码中具体分析!
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#define NUM 10
int main()
{int Y_arr[NUM][NUM] = { 0 };int row = 0;int col = 0;//输入行 列scanf("%d %d", &row, &col);//输入数组中的元素for (int i = 0; i < row; i++){for (int j = 0; j < col; j++){scanf("%d", &Y_arr[i][j]);}}//输入要查找的数int search = 0;scanf("%d", &search);//开始查找for (int i = 0; i < row; i++){int left = 0;int right = col - 1;while (left <= right){int mid = left + (right - left) / 2;if (Y_arr[i][mid] < search)//中数小于要查找的数,更新左下标,缩小范围{left = mid + 1;}else if (Y_arr[i][mid] > search)//中数大于要查找的数,更新右下标,缩小范围{right = mid - 1;}else//找到了{printf("要查找的数的行下标是 %d , 列下标是 %d\n", i, mid);return 0;}}}printf("找不到\n");return 0;
}3.2.2:时间复杂度分析
最坏的情况下,此方法的时间复杂度是 O( row * log(col) )。
仍不符合题目要求。
再优化!
3.3:定位查找法
3.3.1:规律总结
每次从右上角开始查找:
Ⅰ:若要查找的数大于每次的右上角的数,就更新行数。
Ⅱ:若要查找的数小于每次的右上角的数,就更新列数。
3.3.2:画图分析 | 模拟查找
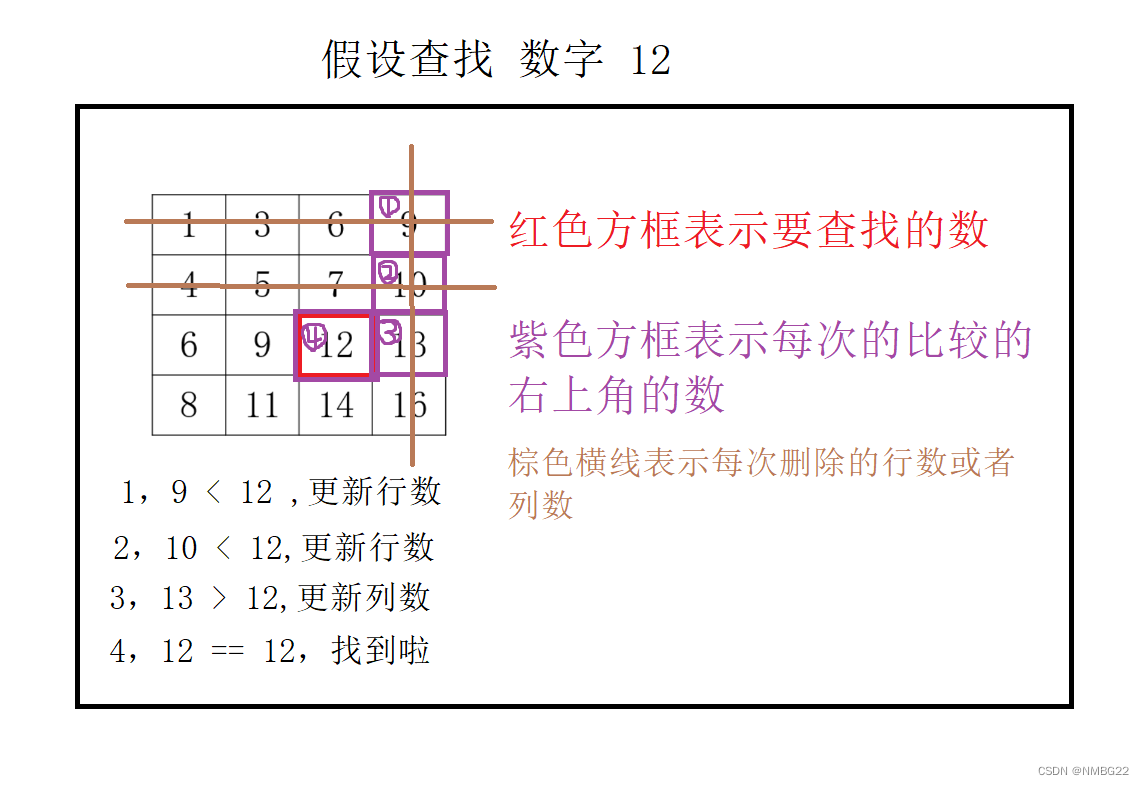
3.3.3:代码解决
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#define NUM 10
int main()
{int Y_arr[NUM][NUM] = { 0 };int row = 0;int col = 0;//输入行 列scanf("%d %d", &row, &col);//输入数组中的元素for (int i = 0; i < row; i++){for (int j = 0; j < col; j++){scanf("%d", &Y_arr[i][j]);}}//输入要查找的数int search = 0;scanf("%d", &search);//开始查找int temp_row = 0;int temp_col = col - 1;while (temp_row < row && temp_col >= 0){if (Y_arr[temp_row][temp_col] > search){temp_col -= 1;}else if (Y_arr[temp_row][temp_col] < search){temp_row += 1;}else{printf("要查找的数的行下标是 %d , 列下标是 %d\n", temp_row, temp_col);return 0;}}printf("找不到\n");return 0;
}3.3.4:时间复杂度分析
最坏的情况下,此方法的时间复杂度为 O( row + col ).
符合题目要求。
完美!!!
四,总结
4.1:问题解决
Ⅰ,同一种问题的解决,可能会使用多种方法,尽我们所能地使用最优解,这是再好不过了。
Ⅱ,不断地优化代码,不断地学习新方法,时时刻刻在进步。
Ⅲ,欢迎分享,感谢阅读!
这篇关于[C语言][C++][时间复杂度详解分析]二分查找——杨氏矩阵查找数字详解!!!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





