本文主要是介绍第11章Stata回归诊断与应对，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
目录
11.1异方差检验与应对
案例延伸
11.2自相关检验与应对
案例延伸
11.3多重共线性检验与应对
案例延伸
在上以讲中，简要介绍了最小二乘线性回归，这种方法可以满足大部分的研究需要。但是这种分析方法的有效性建立在变量无异方差、无自相关、无多重线共线性的基础之上。显示生活中很多数据是不满足这些条件的。那就需要用到在本章中介绍的回归诊断与应对方法。本节内容包括三部分，分别是异方差检验与应对、自相关检验与应对、多重先行检验与应对等方法的应用。
11.1异方差检验与应对
在标准的线性回归模型中，有一个基本假设，整个总体同方差（也就是因变量的变异）不随自身预测值以及其他自变量的值的变化而变化。然后，在实际问题中这一假设条件往往不被满足，会出现异方差的情况，如果继续采用标准的线性回归模型，就会使结果偏向于变异较大的数据，从而发生较大的偏差，所以在进行回归分析是往往需要检验变量的异方差从而提出针对性的解决方案。常用的用于判断数据是否存在异方差的检验方法有绘制残差序列图、怀特检验、BP检验等，解决一方法的方法有使用文件的标准差进行回归以及使用加权最小而成回归分析方法进行回归等。
数据（案例11.1）是某足球俱乐部拥有自己的一套球员评价体系，他们搜集并整理了其中145名球员的相关数据。表中的内容包括球员的身价、身体情况、精神状况、能力情况、潜力情况，试以球员的身价作为因变量，身体情况、精神状况、能力情况、潜力情况作为自变量，对这些数据使用最小而成回归分析方法进行研究，并进行异方差检验，建立合适的回归方程模型用于描述变量之间的关系。
summarize V1-V5,detail #本命令的含义是对数据进行描述性统计分析，从整体上探索数据特征，观测数据是否存在极端数据或者变量间的量纲差距过大，从而可能会对回归分析结果造成不利影响。
correlate V1-V5 #本命令旨在对数据进行相关性分析
regress V1-V5 #本命令旨在对数据进行回归分析，探索自变量对因变量的影响情况
vce #本命令旨在获得变量的方差、协方差矩阵
我们可以看到各个变量的方差、协方差并不是很大。
test V2 V3 V4 V5 #本命令旨在检验回归分析获得的各个变量系数的显著性。
我们可以看到模型非常显著在5%的显著性水平上通过了检验。
predict yhat #旨在获得因变量的拟合值predict e,resid #旨在获得回归模型的估计残差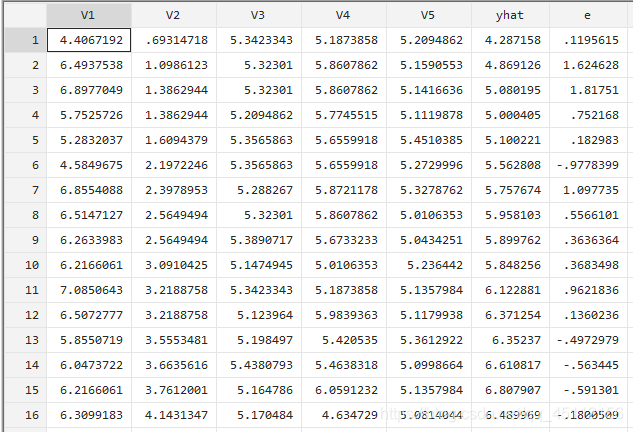
rvfplot #本命令旨在绘制残差与回归的到的拟合值的散点图，从而探索数据是否存在异方差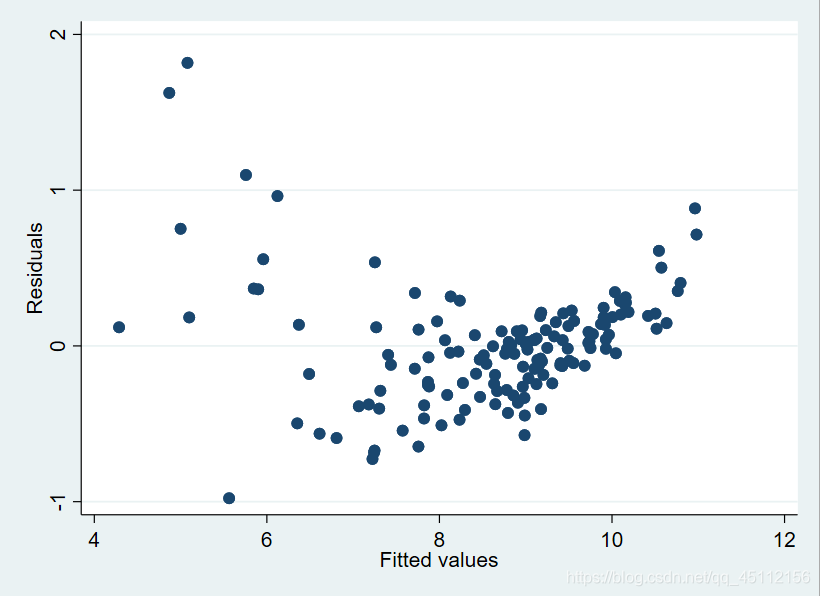
从上图我们可以看出，残差值随着拟合值的不同而有所不同，尤其是在拟合值较小（4-8）的时候，残差波动比较剧烈(并不是在0附近)，所以，数据是存在异方差的。
rvpplot V2 #本命令旨在绘制残差与解释变量V2的散点图，从而探索数据是否u才能在异方差。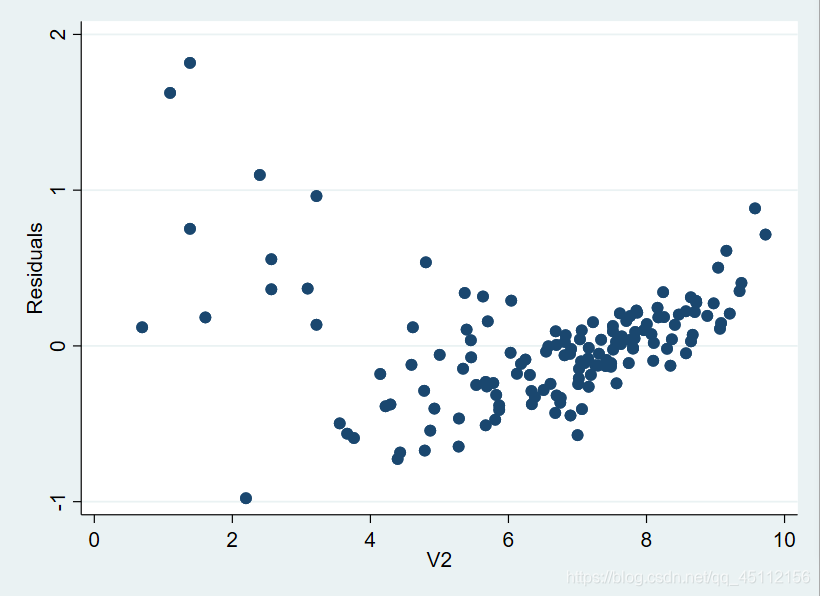
从上图我们可以看出，残差值随着解释变量V2的不同而有所不同，尤其是在拟合值较小（0-4）的时候，残差波动比较剧烈(并不是在0附近)，所以，数据是存在异方差的。
estat imtest,white #本命令为怀特检验，旨在检验数据是否存在异方差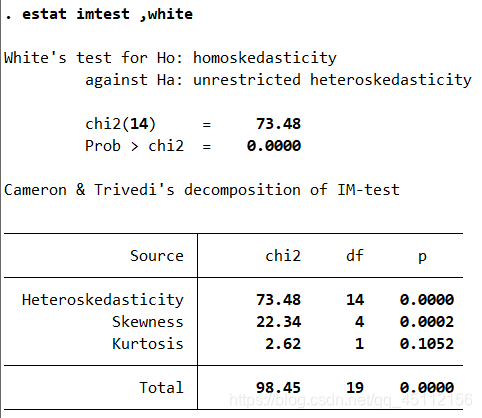
怀特检验的原假设数据为同方差，从上图可以看出P=0.0000，非常显著的拒绝了同方差的原假设，认为存在异方差
estat hettest,iid #本命令为BP检验，旨在使用得到的拟合值来检验数据是否存在异方差
estat hettest ,rhs iid #本命令为BP检验，旨在使用方程右边的解释数据来检验变量是否存在异方差
estat hettest V2,rhs iid #旨在使用指定的技术数据V2来检验变量是否存在异方差。
上面三个检验我们可以看到P值=0.0000，非常显著的拒绝了原假设。认为数据存在异方差
regress V1-V5,robust #本命令为采用文件的标准差对数据进行回归分析，克服数据的异方差对最小二乘回归分析造成的不利影响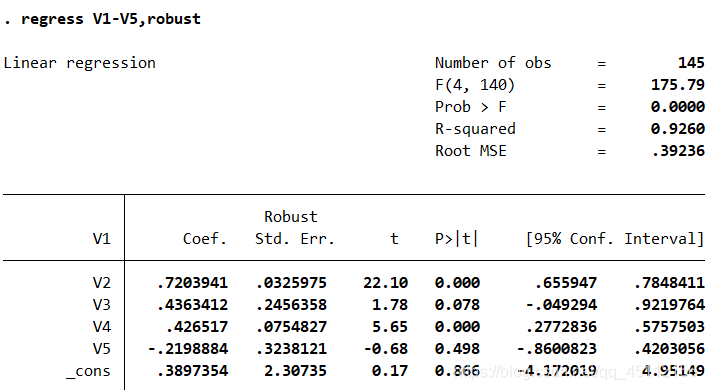
从上图我们可以看到，较最初的回归分析，V3、V5等变量的系数显著性得到了一定程度的提高，这说明通过使用文件的标准差进行回归分析，使模型得到了一定程度的改善。
案例延伸
下面使用最小二乘回归分析方法解决数据的异方差问题。
reg V1-V5 #本命令旨在对5个变量进行最小二乘回归分析predict e,resid #本命令旨在估计上部回归分析结果得到残差gen ee=e^2 #本命令旨在对数据进行平方变换产生新的变量为e的平方gen lnee=log(ee) #本命令旨在对数据进行对数变换，产生新的变量lnee为上部得到残差平方的对数值reg lnee V2，nocon #本命令旨在进行以上部得到的残差平方对数值为因变量，以V2 为自变量，并且不包含常数项的最小二乘回归分析predict yhat #本命令旨在预测上步进行的最小二乘回归产生的因变量的拟合值gen yhathat=exp(yhat) #本命令旨在对因变量的拟合值进行指数变换，产生新的值yhathat为yhat的指数值reg V1 V2 V3 V4 V5 [aw=1/yhathat] #本命令旨在对数据进行以V1为因变量以V2 V3 V4 V5 为自变量，以yhathat的倒数为权重变量的加权最小而成回归分析结论：进行了加权最小二乘回归分析后我们可以明显的看到，模型的F值（代表模型的显著程度）、部分变量的P值以及R-squared值、Adj R-squared值(代表模型的解释能力)都较普通的最小二乘回归分析有了一定程度的优化，这就是克服异方差带来的改善效果。
11.2自相关检验与应对
如果线性相关模型中的随机误差项的各期望值之间存在着相关关系，这时，我们就称随机误差项之间存在自相关性。线性回归模型中随机误差项存在序列相关的原因很多，但主要是由经济变量的自身特点、数据特点、变量选择及模型函数的形成选择引起的。常见原因包括经济变量的惯性作用、经济行为的滞后性、一些随机因素的干扰或影响、模型设定误差、观测数据处理等。自相关不会影响到最小二乘估计量的线性和无偏性，但会使之失去有效性，使之不再是最优估计值量，而且自相关的系数估计量将有相当大的方差，T检验也不再显著，模型的预测功能失效，所以在进行回归分析是往往需要检验数据得自相关性，从而提出针对性的解决方案。常用的用于判断数据是否存在自相关的检验方法由绘制残差序列图、BG检验、Box-Pierce检验、DW检验等，解决自相关的方法有使用自相关异方差文件的标准差进行回归以及使用广义最小二乘回归分析方法进行回归。
数据（案例11.2）给出了某企业经营利润和经营资产的有关数据，试使用经营利润作为因变量，以经营资产作为自变量，对这些数据使用最小二乘回归分析的方法进行研究，先进性自相关检验，最终建立合适的回归方程模型用于描述变量之间的关系。
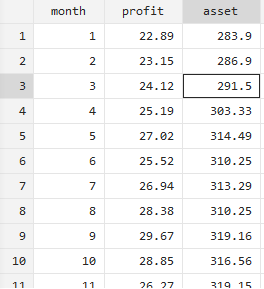
summarize month profit asset,detail #本命令旨在对数据进行描述性分析，从整体上探索数据特征，观测其是否存在极端数据或者变量间的量纲差距过大，从而可能会对回顾hi分析结果造成不利影响correlate month profit asset #对三个变量进项相关性分析regress profit asset #以profit为因变量，asset为自变量进行回归分析vce #获得变量的方差-协方差矩阵test asset #旨在检验回归分析获得的各个变量系数的显著性predict yhat #本命令旨在获得因变量的拟合值predict e,resid #本命令旨在获得回归模型的估计残差上述命令结果在前面章节详细讲述过不再过多赘述
tsset month #本命令旨在把数据定义为以month为周期的时间序列关于时间序列的相关概念与分析方法等，将在后续章节中详细进行说明，这里不再赘述。
scatter e l.e #本命令旨在绘制残差与残差滞后一期的散点图，用于探索数据是否存在一阶自相关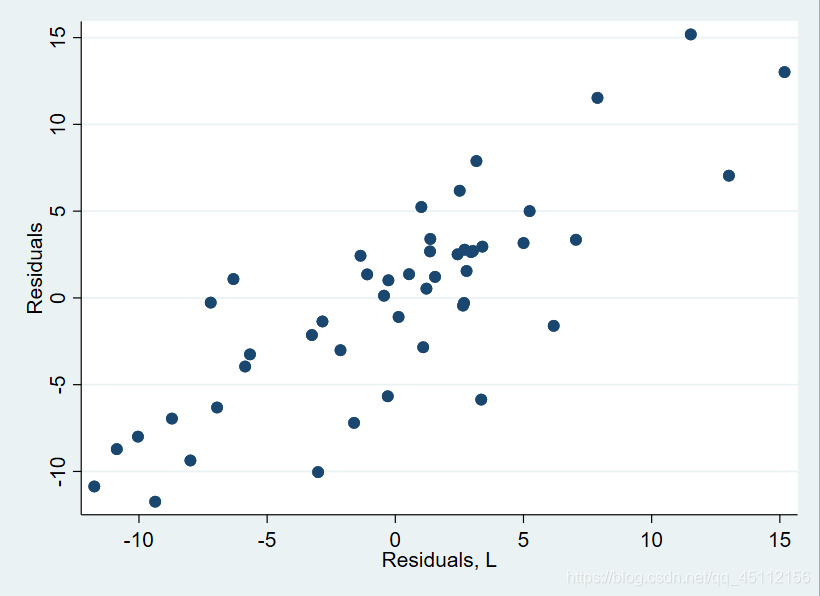 
残差与滞后一期的残差之间存在着一种类似正向线性变动关系，所以数据是存在自相关的。
ac e #旨在绘制残差的自相关图，用于探索其自相关阶数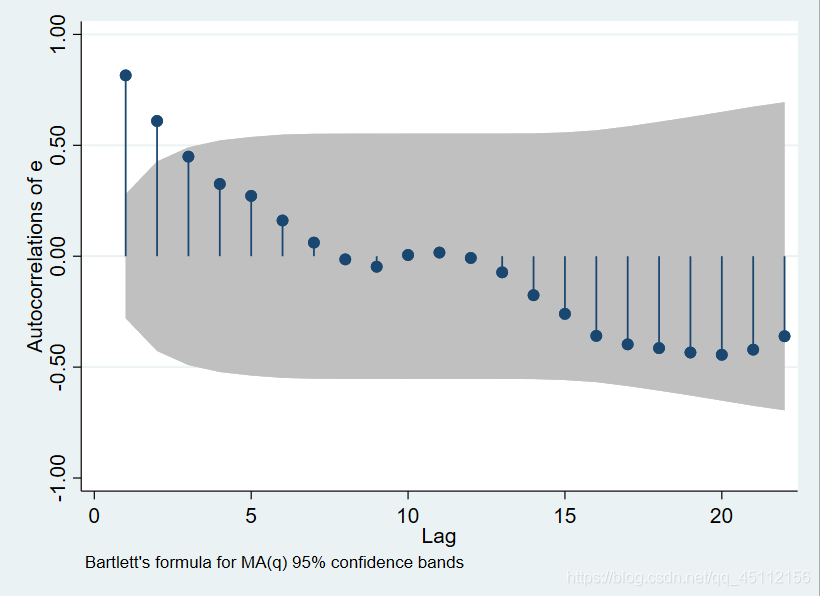
图中横轴代表滞后阶数，阴影部分表示95%的自相关置信区间，在阴影部分之外表示自相关系数显著部位0.从图中可以看出数据主要存在一阶自相关。
pac e #本命令旨在绘制残差的偏自相关图，用于探索其自相关阶数
图中横轴表示滞后阶数，阴影部分表示95%的自相关置信区间，在阴影部分之外表示自相关系数显著部位0，从上图同样可以看出，数据主要存在一阶自相关。
estat bgodfrey #本命令为BG检验、旨在检验残差自相关性
BG检验的原假设是数据没有自相关。从图中可以看出P值为0.0000，非常显著的拒绝了没有自相关的假设，认为存在自相关。
wntestq e #本命令为Box-Pierce检验，旨在检验残差自相关性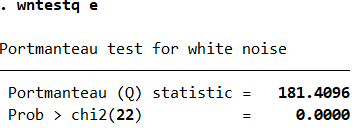
Box-Pierce Q检验的原假设是数据没有自相关，从图中可以看出决绝了原假设，说明数据存在自相关。
estat dwatson #本命令为DW检验，旨在检验残差自相关性
DW检验的原假设数据没有自相关，从图中可以看出，DW的值为0.3545385，远远小于无自相关的值2，所以认为存在正的自相关。
di 49^0.25 #本命令为计算样本个数1/4次幂，旨在确定使用异方差自相关文件的标准差进行回归的滞后阶数。
本例中样本个数为49个，49的0.25次方是2.6457513，所以确定的滞后阶数是3
newey profit asset,lag(3) #本命令为采用异方差自相关稳健的标准差对数据进行回归分析，克服数据的自相关性对最小二乘回归分析造成的不利影响。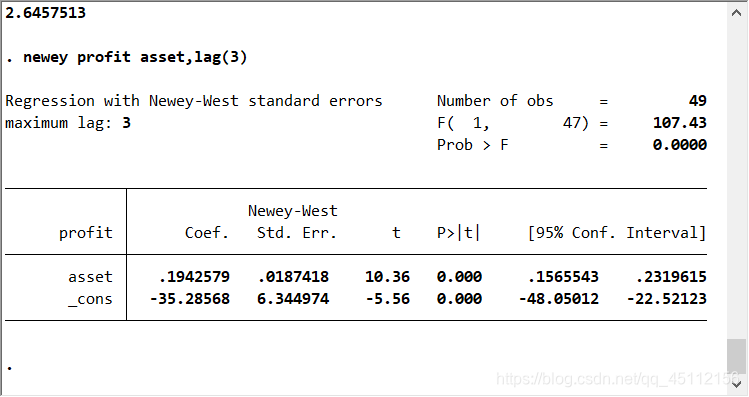
从上图可以看出，模型的整体显著性、自变量与常数项系数的显著性以及模型的解释能力依旧很高。
案例延伸
下面使用广义二乘回归分析方法解决数据的异方差。
prais profit asset,corc #本命令旨在对数据进行迭代式CO估计法广义最小二乘回归分析。
上图结果与前面解读类似，不再过多赘述。不过值得注意的是DW值从0.254538跃升至1.927109，非常接近没有自相关时多的值2，所以经过co迭代变换后，模型消除了自相关，但是模型的显著成都和解释能力都有所下降。
prais profit asset,nolog #本命令旨在对数据进行迭代式PW估计发广义最小二乘回归分析。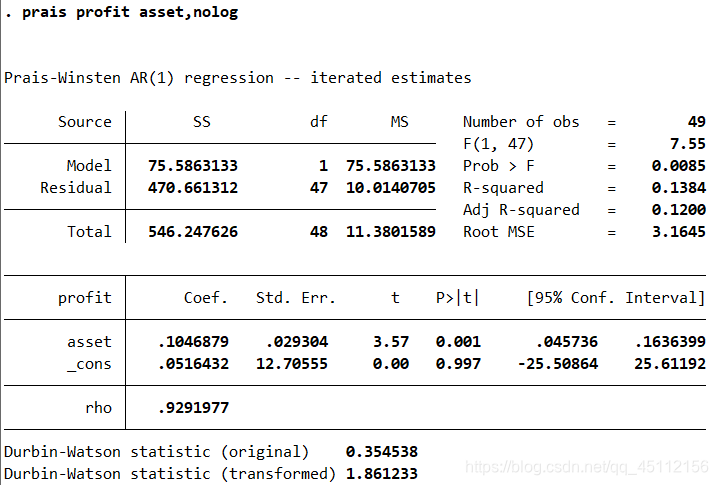
结果不再过多赘述。
11.3多重共线性检验与应对
多重共线性包括严重的多重共线性和近似的多重共线性。在进行回归分析师，如果某一自变量可以被其他的自变量通过线性组合得到，那么数据就存在严重的多重共线性问题。近似的多重共线性是指某自变量能够被其他的自变量较多的解释，或者说自变量之间存在着很大的信息重叠。在数据存在多重共线性的情况下，最小二乘回归分析得到的系数值仍然是最优无偏估计的，但是会导致系数的估计值不准确，而且会使部分系数的显著性很弱，也不好区分每个自变量对因变量的影响程度。解决多重共线性的办法通常有两种：一种是提出不显著的变量；另一种是进行因子分析提取出相关性较弱的几个主因子再进行回归分析。
数据（案例11.3）给出了我国1996年-2003年国民经济主要指标统计数据。试着使用国内生产总值作为因变量，以货物周转量、原煤、发电量、原油等作为自变量，对这些数据使用最小二乘回归分析的方法进行分析，并进行多重共性检验，最终建立合适多的回归方程用于描述变量之间的关系。
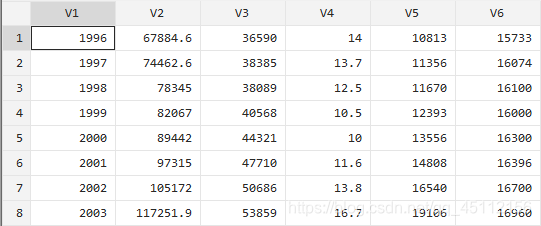
summarize V1 V2 V3 V4 V5 V6 ,detail #对6个变量进行描述性统计分析correlate V1-V6 #对各个变量进行相关性分析，尤其是因变量和自变量之间的相关性关系regress V2 V3 V4 V5 V6 #在数据上进行回归分析，探索自变量对因变量的影响情况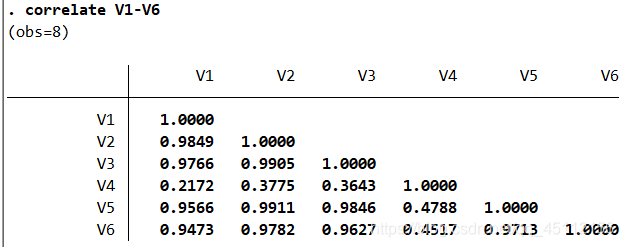 
我们可以看到变量之家的相关系数是非常大的，这就意味着变量间存在很高程度的信息重叠，模型很有可能存在多重共线性问题。
从上面可以看出，国内生产总值与货物周转量、原煤、发电量、原油等变量进行回归得到的模型中部分变量的系数非常不显著，而且原煤产量的系数居然是负值，这显然是不符合现实情况的，造成这些现象的根源就在于模型存在着程度比较高的多重共线性问题。
estat vif #本命令旨在对数据进行多重共线性检验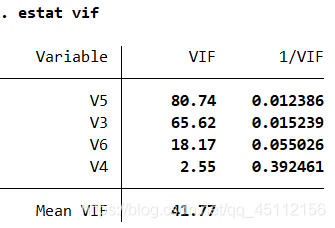
从图中可以看出。Mean VIF的值是41.77，远远大于合理值10 ，所以模型存在较高程度的多重共线性，其中V5的方差膨胀因子最高，即80.74，所以需要讲V5剔除以后重新进行回归。
regress V2 V3 V4 V6 #对4个变量进行回归分析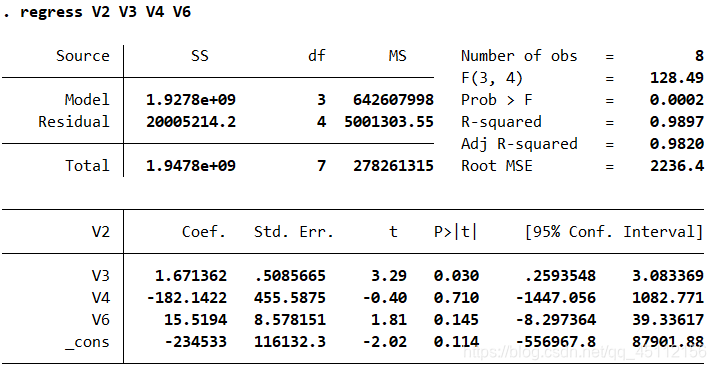
estat vif regress V2 V3 V4estat vif regress V2 V3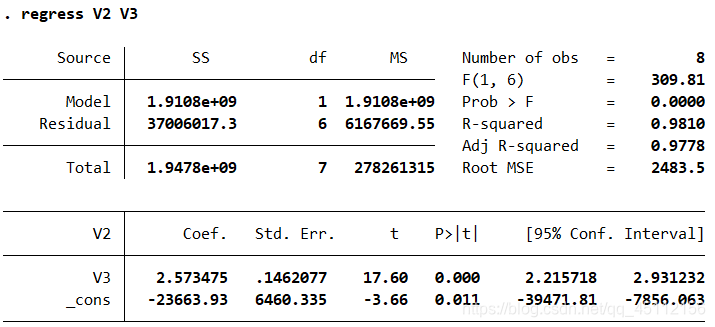
最终结论是参与分析的变量，货物周转量能够最大程度地解释国内生产总值，货物周转量越大，国内生产总值越大。
案例延伸
下面使用因子分析方法解决模型地多重共线性问题
factor V3 V4 V5 V6 ,pcf #本命令旨在对4个变量提取公因子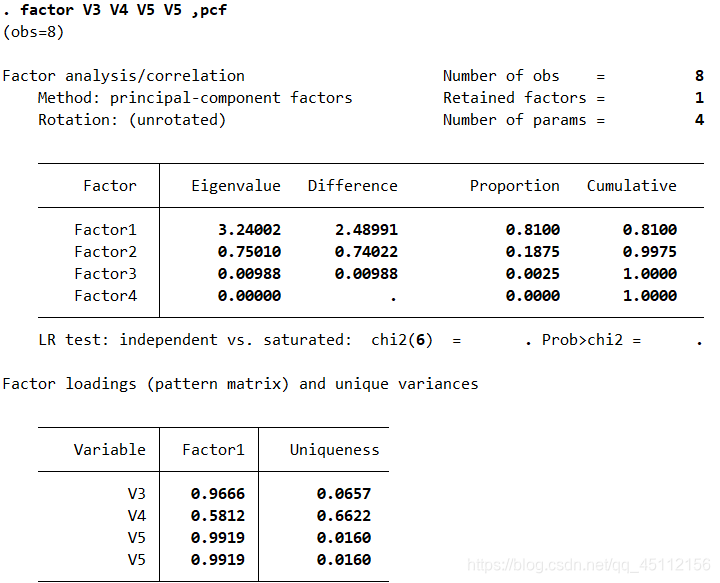
结果不再过多赘述。
predict f1 #本命令旨在产生已提取地公因子变量f1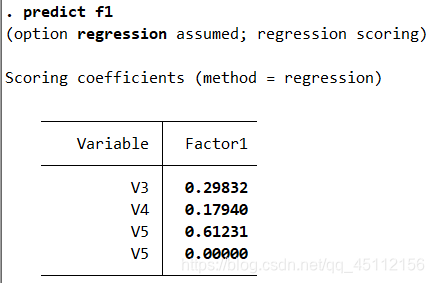
这个展示地是因子得分系数矩阵，可以写出公因子表达式。值得一提地是在表达式中各个变量已经不是原始变量，而是标准化变量。表达式如下
f1=0.3018*货物周转量+0.18001*原煤+0.30919*发电量+0.30556*原油
regress V2 f1 #对两个变量进行回归分析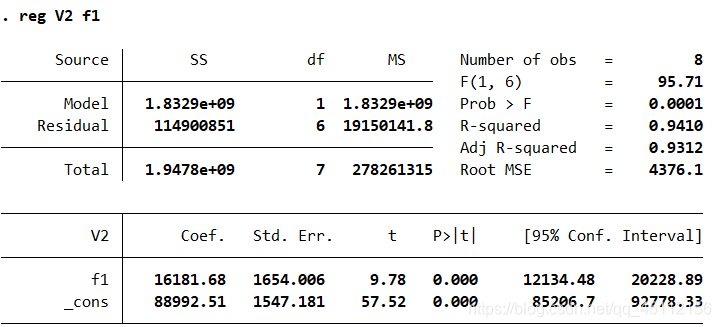 
可以看出模型地解释能力、模型地显著性、模型中各个变量和常数项地系数都达到了几乎完美的状态。
vif #本命令旨在对模型进行多重共线性检验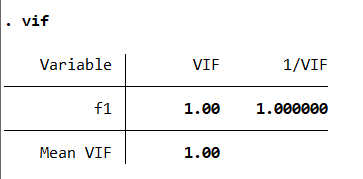
从图中我们可以看出，Mean VIF的值是1，远远小于合理值10，所以模型的多重共线性得到了很大程度的改善。
这篇关于第11章Stata回归诊断与应对的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
