本文主要是介绍Python实现基于多元线性回归模型进行统计学相互作用和方差分析(anova算法)项目实战,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
说明:这是一个机器学习实战项目(附带数据+代码+文档+视频讲解),如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景
多元线性回归模型(Multiple Linear Regression Model)是一种统计学方法,用于研究一个或多个自变量(predictors)与因变量(dependent variable)之间的关系。在模型中,因变量的值通过一个线性函数来预测,该函数包含了自变量的系数和截距项。
相互作用(Interaction)是指模型中的两个或多个自变量之间存在一种依赖关系,即一个自变量对因变量的影响程度取决于另一个自变量的取值。在多元线性回归中,如果存在显著的交互效应,意味着简单的主效应并不能完全描述自变量对因变量的影响,需要考虑自变量之间的联合效应。
例如,在一个包含两个自变量 X1 和 X2 的模型中,可能存在一个交互项 X1*X2。这意味着对于给定的 X1 值,X2 对因变量的影响可能随着 X1 的变化而变化,反之亦然。
方差分析(ANOVA,Analysis of Variance)在多元线性回归模型中主要用于检验不同组别或条件下的均值差异是否显著。当模型包含分类变量,并且我们想探究这些分类变量的不同水平(或它们与其他连续变量的交互作用)是否对因变量有显著影响时,可以使用方差分析。
在多元线性回归框架下,可以通过 F 检验或者anova表来评估各个自变量、交互项以及误差项对总变异性贡献的显著性。这样就可以确定哪些自变量及其交互项对因变量有显著影响,并进一步解释模型的预测能力。
本项目通过OLS回归算法来构建线性回归模型进行统计学相互作用和方差分析。
2.数据获取
本次建模数据来源于网络(本项目撰写人整理而成),数据项统计如下:
| 编号 | 变量名称 | 描述 |
| 1 | S | 工资 |
| 2 | X | 经验(年) |
| 3 | E | 教育(1=学士,2=硕士,3=博士) |
| 4 | M | 管理(1=管理,0=非管理) |
数据详情如下(部分展示):

3.数据预处理
3.1 用Pandas工具查看数据
使用Pandas工具的head()方法查看前五行数据:

关键代码:

3.2 数据缺失查看
使用Pandas工具的info()方法查看数据信息:

从上图可以看到,总共有4个变量,数据中无缺失值,共46条数据。
关键代码:

3.3 数据描述性统计
通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。
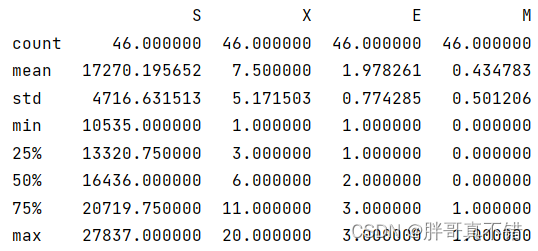
关键代码如下:

4.探索性数据分析
4.1 变量直方图
用Matplotlib工具的hist()方法绘制直方图:

从上图可以看到,变量主要集中在12500~27500之间。
4.2 相关性分析

从上图中可以看到,数值越大相关性越强,正值是正相关、负值是负相关。
4.3 绘制散点图

5.构建线性回归模型
主要使用OLS回归算法,用于目标回归。
5.1 构建模型
| 编号 | 模型名称 | 参数 |
| 1 | OLS回归模型 | 默认参数 |
5.2 模型摘要信息

5.3 影响力摘要信息
影响力指标部分数据展示:
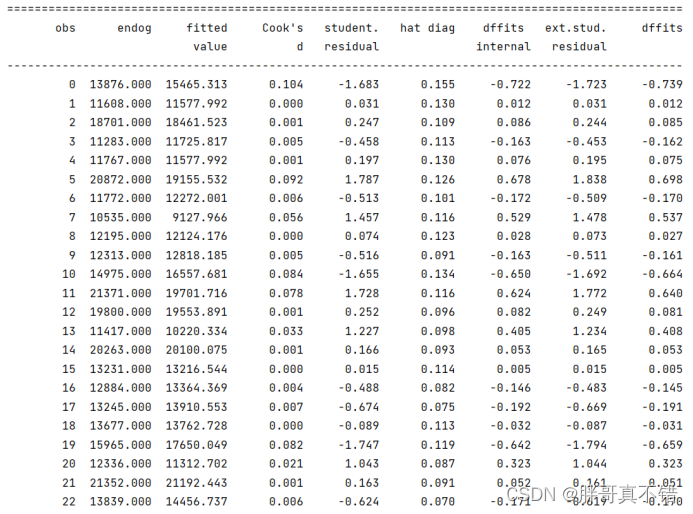
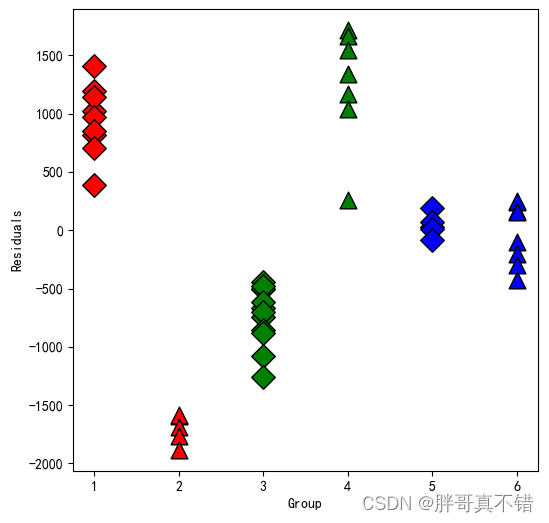
5.4 残差散点图
5.5 模型摘要信息
把"E" 和 "X" 的乘积作为模型的一个特征项,进行建模。

5.6 方差分析结果

5.7 模型摘要信息
把"E" 和 "M" 的乘积作为模型的一个特征项,进行建模。

5.8 方差分析结果

5.9 学生化残差散点图

6.模型评估
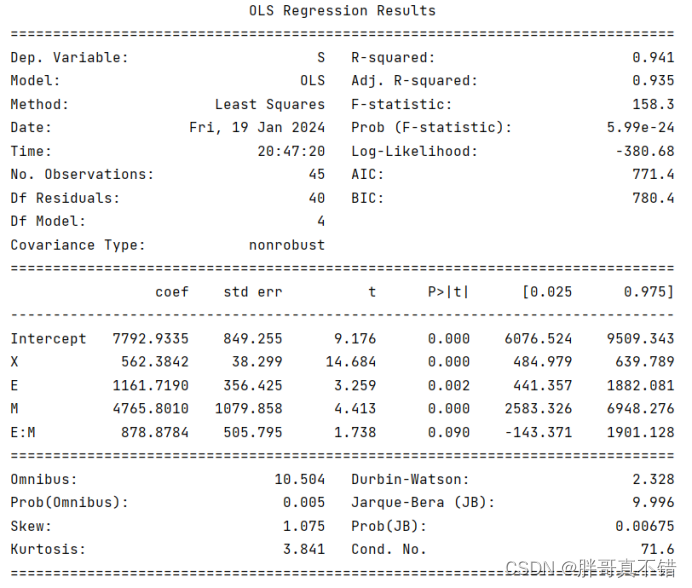
6.1 模型摘要信息
E、 X 、 M三个特征建模。

6.2 模型摘要信息
把"E" 和 "X" 的乘积作为模型的一个特征项,进行建模。

6.3 方差分析结果

6.4 模型摘要信息
把"E" 和 "M" 的乘积作为模型的一个特征项,进行建模。
6.5 方差分析结果

6.6 标准残差散点图
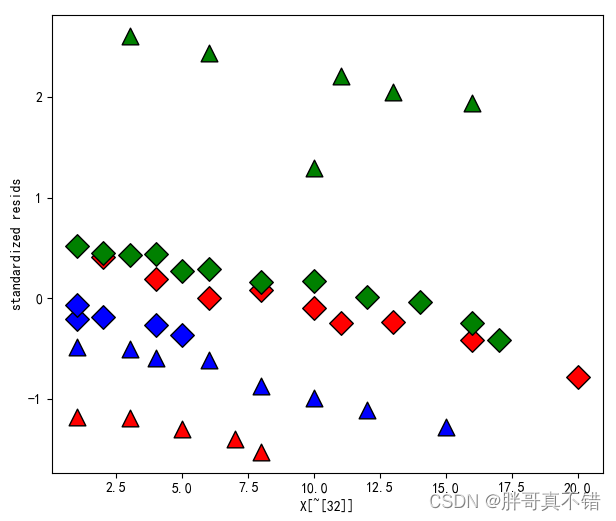
6.7 特征散点图
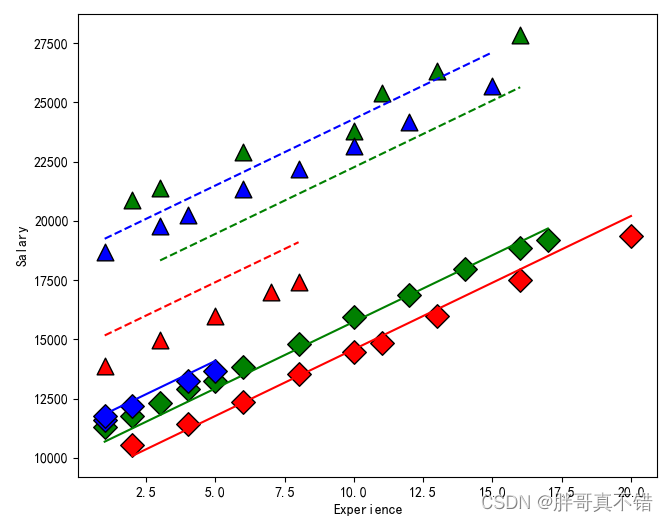
6.8 相互作用图

7.结论与展望
综上所述,本文采用了OLS算法来构建回归模型进行方差分析和相互作用分析,最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。
# 本次机器学习项目实战所需的资料,项目资源如下:# 项目说明:# 获取方式一:# 项目实战合集导航:https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2# 获取方式二:链接:https://pan.baidu.com/s/1JJoLP6MbnJXAnBrpjRpNHA
提取码:vnqh这篇关于Python实现基于多元线性回归模型进行统计学相互作用和方差分析(anova算法)项目实战的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





