本文主要是介绍运动模型非线性测量非线性扩展卡尔曼跟踪融合滤波算法(Matlab仿真),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
卡尔曼滤波的原理和理论在CSDN已有很多文章,这里不再赘述,仅分享个人的理解和Matlab仿真代码。
之前的博文运动模型非线性扩展卡尔曼跟踪融合滤波算法(Matlab仿真)-CSDN博客使用扩展卡尔曼滤波算法将非线性的运动模型线性化,但测量值仍旧是线性的,不需要雅可比矩阵。这里考虑测量值也为非线性的情况,并用Matlab做仿真。
如果估计值为[x,y,v,theta,w],测量值为[x,y,v,theta],则它们为线性关系,状态观测矩阵可以用下面的矩阵表示。

这里考虑估计值为[x,y,v,theta,w],但测量值为[x,y,vx,vy],两者为非线性关系,则需要使用下表中的h(x)和线性化的雅可比矩阵![]() 进行滤波计算。
进行滤波计算。

由估计值和测量值的关系可以得到
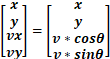
也即h(x)函数,写为测量的预测则为
% 扩展卡尔曼滤波的测量模型
function Z_pred = EKF_measure(x)Z_pred = x(1:4);v = x(3);theta = x(4);Z_pred(3) = v*cos(theta);Z_pred(4) = v*sin(theta);
end 而对于测量的雅可比矩阵![]() ,则可以通过下式获得
,则可以通过下式获得

根据公式计算,得到测量的雅可比矩阵为

再带入H矩阵中可以得到扩展卡尔曼滤波的结果。将上述公式用matlab编程即可得到滤波结果。
% 匀速转弯运动模型的扩展卡尔曼滤波算法仿真
% 摄像头和雷达的测量值为x,y,vx,vy,有J_H
clc;clear;close all;% 匀速转弯运动的初始值
x0 = 0; % 目标的初始横向位置
y0 = 0; % 目标的初始纵向位置
v = 3; % 目标的速度
theta = 0; % 目标的偏航角(目标在当前坐标系下和x轴的夹角)
omga = 0.1; % 目标的偏航角速度
N = 150; % 数据量
dt = 0.2; % 单帧时间
t = dt*(1:1:N); % 时间轴% 更新超参数
sigma_q_x = 0.2; % 纵向距离的过程噪声标准差
sigma_q_y = 0.2; % 横向距离的过程噪声标准差
sigma_q_v = 0.2; % 目标速度的过程噪声标准差
sigma_q_theta = 0.01; % 目标偏航角的过程噪声标准差
sigma_q_ogma = 0.01; % 目标偏航角速度的过程噪声标准差
Q_matrix_ctrv = diag([sigma_q_x^2, sigma_q_y^2, sigma_q_v^2, sigma_q_theta^2, sigma_q_ogma^2]);% 设置测量噪声协方差矩阵R,噪声来自测量的误差
sigma_r_x = 0.2;
sigma_r_y = 0.2;
sigma_r_vx = 0.1;
sigma_r_vy = 0.1;
R_matrix_ctrv = diag([sigma_r_x^2, sigma_r_y^2, sigma_r_vx^2, sigma_r_vy^2]);% 卡尔曼滤波器初始化参数
X_ctrv = zeros(5,N); % 初始化目标运动真值
W_cv = mvnrnd(zeros(1,5), Q_matrix_ctrv)'; % 过程噪声向量
X_ctrv(:,1) = EKF_predict([x0;y0;v;theta;omga], dt); % 根据运动模型得到当前时刻状态
X_ctrv(:,1) = X_ctrv(:,1) + W_cv; % 加过程噪声,也可不加
Z_ctrv = zeros(4,N); % 初始化目标测量值
V_ctrv = mvnrnd(zeros(1,4), R_matrix_ctrv)'; % 观测误差矩阵
Z_ctrv(:,1) = EKF_measure(X_ctrv(:,1)) + V_ctrv;
Xest_ekf = zeros(5,N); % 卡尔曼滤波估计值
Xest_ekf(:,1) = X_ctrv(:,1); % 第一帧无法滤波,用测量值初始化
P_ekf = zeros(5,5,N); % 状态估计协方差矩阵
P_ekf(:,:,1) = eye(5); % 初始化状态估计协方差矩阵,常用单位矩阵% 扩展卡尔曼滤波的核心算法
for i = 2:N% 状态更新X_ctrv(:,i) = EKF_predict(X_ctrv(:,i-1), dt);W_ctrv = mvnrnd(zeros(1,5), Q_matrix_ctrv)'; % 过程噪声向量X_ctrv(:,i) = X_ctrv(:,i) + W_ctrv; % 加过程噪声% 预测步骤X_pre = EKF_predict(Xest_ekf(:,i-1), dt);F_ctrv = EKF_Jacobian_F(Xest_ekf(:,i-1), dt);P_pre = F_ctrv * P_ekf(:,:,i-1) * F_ctrv' + Q_matrix_ctrv;% 测量模型更新V_ctrv = mvnrnd(zeros(1,4), R_matrix_ctrv)'; % 观测误差矩阵Z_ctrv(:,i) = EKF_measure(X_ctrv(:, i)) + V_ctrv;% 更新步骤H_ctrv = EKF_Jacobian_H(X_ctrv(:, i));K_ekf = P_pre * H_ctrv' / (H_ctrv * P_pre * H_ctrv' + R_matrix_ctrv);Xest_ekf(:,i) = X_pre + K_ekf * (Z_ctrv(:,i) - EKF_measure(X_pre));P_ekf(:,:,i) = (eye(5) - K_ekf * H_ctrv) * P_pre;
end% 绘图部分保持不变
figure;
size = 10;
width = 2;
% 位置曲线图
subplot(2,2,1);
plot(Z_ctrv(1,:),'.g','MarkerSize',size); hold on; % 画出测量值
plot(Xest_ekf(1,:),'b','LineWidth',width);hold on; % 画出最优估计值
plot(X_ctrv(1,:),'r','LineWidth',width); % 画出实际状态值
title('X位置状态曲线');
legend('位置测量值', '位置最优估计值', '实际位置');% 位置曲线图
subplot(2,2,2);
plot(Z_ctrv(2,:),'.g','MarkerSize',size);hold on; % 画出测量值
plot(Xest_ekf(2,:),'b','LineWidth',width);hold on; % 画出最优估计值
plot(X_ctrv(2,:),'r','LineWidth',width); % 画出实际状态值
title('Y位置状态曲线');
legend('位置测量值', '位置最优估计值', '实际位置');X_vx_ctrv = X_ctrv(3,:).*cos(X_ctrv(4,:));
X_vy_ctrv = X_ctrv(3,:).*sin(X_ctrv(4,:));
Xest_vx_ekf = Xest_ekf(3,:).*cos(Xest_ekf(4,:));
Xest_vy_ekf = Xest_ekf(3,:).*sin(Xest_ekf(4,:));
% 速度曲线图
subplot(2,2,3);
plot(Z_ctrv(3,:),'.g','MarkerSize',size); hold on; % 画出测量值
plot(Xest_vx_ekf,'b','LineWidth',width); hold on; % 画出最优估计值
plot(X_vx_ctrv,'r','LineWidth',width); % 画出实际状态值
title('X速度状态曲线');
legend('速度测量值', '速度最优估计值', '实际速度');% 偏航角曲线图
subplot(2,2,4);
plot(Z_ctrv(4,:),'.g','MarkerSize',size); hold on; % 画出测量值
plot(Xest_vy_ekf,'b','LineWidth',width); hold on; % 画出最优估计值
plot(X_vy_ctrv,'r','LineWidth',width); % 画出实际状态值
title('Y速度状态曲线');
legend('速度测量值', '速度最优估计值', '实际速度');% 位置平面图
% figure;
% plot(Z_ctrv(1,:),Z_ctrv(2,:));hold on; % 画出测量值
% plot(Xest_ekf(1,:),Xest_ekf(2,:)); % 画出最优估计值
% plot(X_ctrv(1,:),X_ctrv(2,:));hold on; % 画出实际值
% title('目标运动曲线');
% legend('位置测量值', '位置最优估计值', '实际位置');% 扩展卡尔曼滤波的预测模型
function X_pred = EKF_predict(x, dt)% CTRV模型的预测模型v = x(3);theta = x(4);omega = x(5);if omega == 0 % 避免除以0dx = v * cos(theta) * dt;dy = v * sin(theta) * dt;elsedx = v/omega * (sin(theta + omega * dt) - sin(theta));dy = v/omega * (-cos(theta + omega * dt) + cos(theta));enddtheta = omega * dt;X_pred = x + [dx; dy; 0; dtheta; 0]; % 速度和转向率的变化假设为0
end% 扩展卡尔曼滤波预测模型的雅可比矩阵
function F = EKF_Jacobian_F(x, dt)v = x(3);theta = x(4);omega = x(5);F = eye(5);if omega == 0 % 避免除以0F(1, 3) = -v * sin(theta) * dt;F(1, 4) = cos(theta) * dt;F(2, 3) = v * cos(theta) * dt;F(2, 4) = sin(theta) * dt;elseF(1, 3) = 1/omega * (sin(theta + omega * dt) - sin(theta));F(1, 4) = v/omega * (cos(theta + omega * dt) - cos(theta));F(1, 5) = v/omega^2 * (sin(theta) - sin(theta + omega * dt)) + v * dt * cos(theta + omega * dt)/omega;F(2, 3) = v/omega * (sin(theta + omega * dt) - sin(theta));F(2, 4) = 1/omega * (-cos(theta + omega * dt) + cos(theta));F(2, 5) = v/omega^2 * (-cos(theta) + cos(theta + omega * dt)) + v * dt * sin(theta + omega * dt)/omega;endF(4, 5) = dt;
end% 扩展卡尔曼滤波的测量模型
function Z_pred = EKF_measure(x)Z_pred = x(1:4);v = x(3);theta = x(4);Z_pred(3) = v*cos(theta);Z_pred(4) = v*sin(theta);
end% 扩展卡尔曼滤波观测模型的雅可比矩阵
function H = EKF_Jacobian_H(x)H = zeros(4,5);v = x(3);theta = x(4);cos_theta = cos(theta);sin_theta = sin(theta);H(1, 1) = 1;H(2, 2) = 1;H(3, 3) = cos_theta;H(3, 4) = -v*sin_theta;H(4, 3) = sin_theta;H(4, 4) = v*cos_theta;
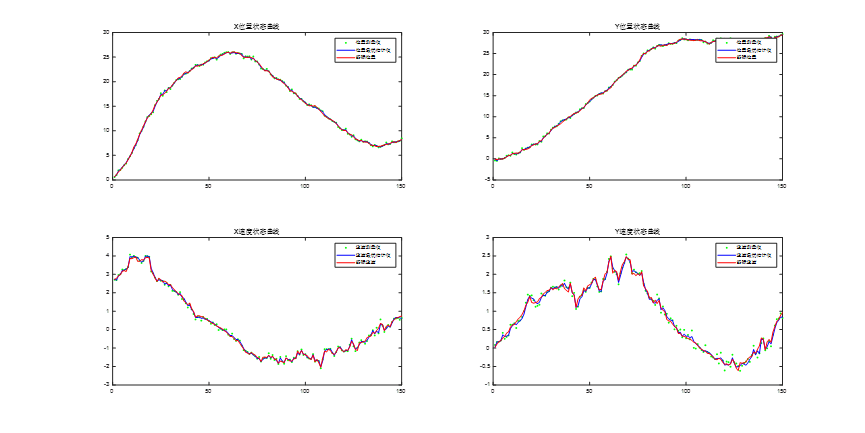
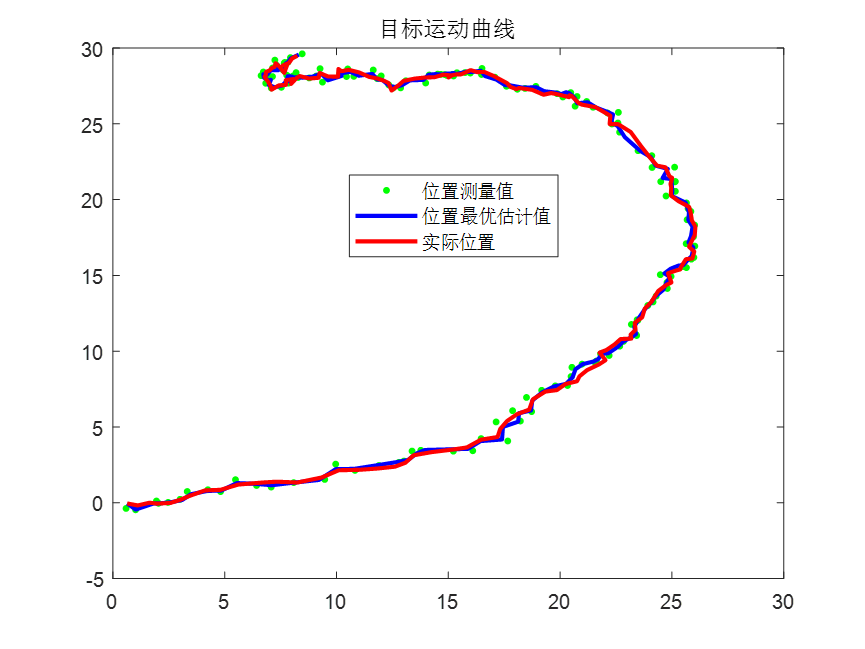
end下图是仿真运行的结果,可以看到匀速转弯运动目标通过扩展卡尔曼滤波算法得到了高精度的跟踪轨迹。
这篇关于运动模型非线性测量非线性扩展卡尔曼跟踪融合滤波算法(Matlab仿真)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








