本文主要是介绍信息熵(下),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
翻译:http://colah.github.io/posts/2015-09-Visual-Information/
如有侵权,请联系我~
小白学习笔记,欢迎大神批评指正~
计算熵
长度为L的信息代价为1/(2^L),根据这个公式可以反算出来信息最好的长度选择L:
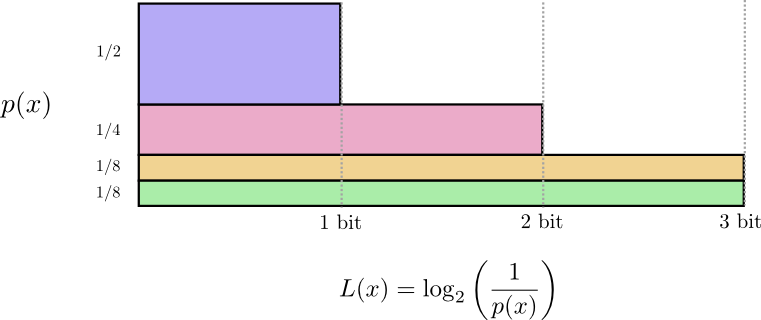
早些时候,我们讨论了利用最可能的编码的平均信息长度的限制,叫做p的熵H(p).

人们通常所说的熵,其实主要是下面这种情形,其实与上面的表达是等价的。

需要进行交流的平均信息量描述了系统的不确定性,并且给出一种量化信息的方式。若我已经确信知道要发生什么,那我就没必要发送所有的信息,若有两件事情以相同的概率发生,我仅需要一位表示,对于一件事情,如果越确定会发生,则可以用较短的信息去表示。
输出的不确定性越大,我需要学习的就越多。
交叉熵
有一天,Tom谈恋爱了,他的女朋友叫Amy,Amy不那么喜欢狗,她更喜欢猫多一些,他们俩的词频出现的概率如下,可以发现,他们喜欢的动物都是相同的,只是Tom喜欢狗多些,Amy喜欢猫多一些:
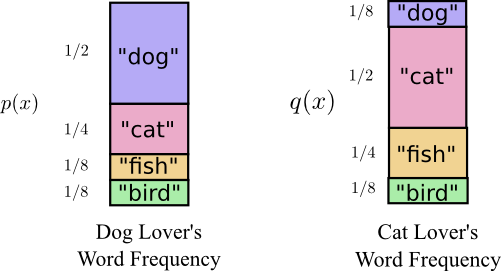
Amy也开始用Tom的编码方式给我写信,但是结果可想而知,Tom的编码方式适合于他自己的概率分布,当然不适用于Amy.当要表达同一件事时候,Tom的平均编码长度为1.75位时,Amy的要2.25位。
我们可以定义公式如下:

等式左边可以定义为交叉熵,如果一件事情,用一个概率分布进行最优编码,用另一个分布来进行交流时,编码的平均长度称为交叉熵。

然后我就跟Amy约定,她用自己的编码方式,这样她给我发的消息就会短一些。但是,有时候调皮的Tom会用Amy的编码格式给我写信。这就尴尬的存在四种可能性,他们可能都各自用各自的编码,也可能用他人的编码:
- Tom用自己的编码(H(p) = 1.75位)
- Amy使用Tom的编码(
 = 2.25位)
= 2.25位) - Amy用自己的编码(H(q) = 1.75位)
- Tom使用Amy的编码(
 = 2.375位)
= 2.375位)
下面的图中,每个子图都表示四种可能性之一,同一个人的情形是上下两个图的对比,同一个编码方式,是左右两个图的对比。
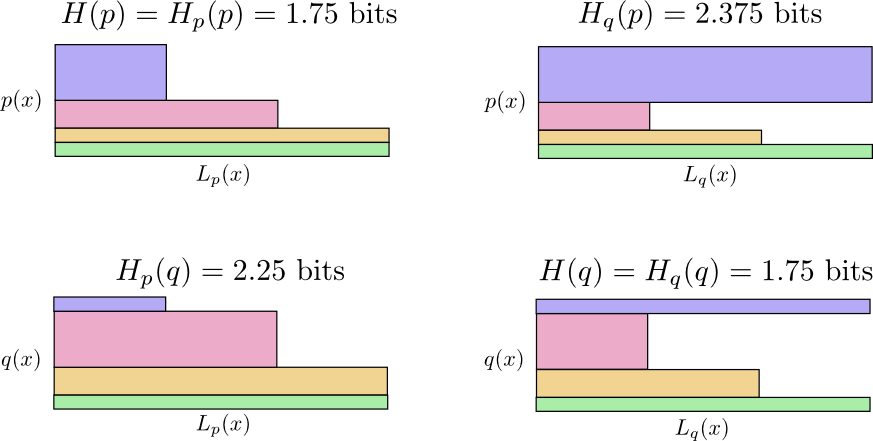
交叉熵不是对称的
交叉熵表达了两个概率分布差异性有多大。两概率分布的差异性越大,交叉熵要比单独一个概率的熵要大的越多,若两个概率分布相同,则熵与交叉熵的差异也会变成0。
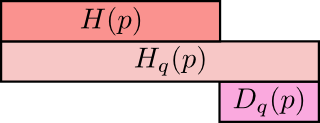
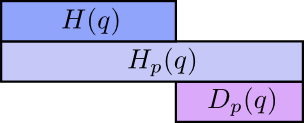
我们称差异为相对熵(**K**ullback-**L**eibler divergence),P关于q的相对熵:

熵与多变量
天气的例子再拿出啦:
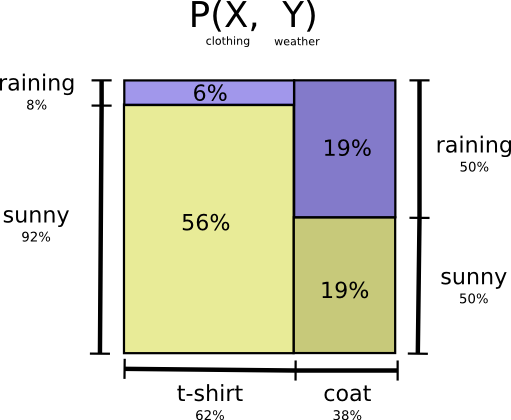
将上面图示的部分,拉直表示为右边的图,可以发现是等价的。
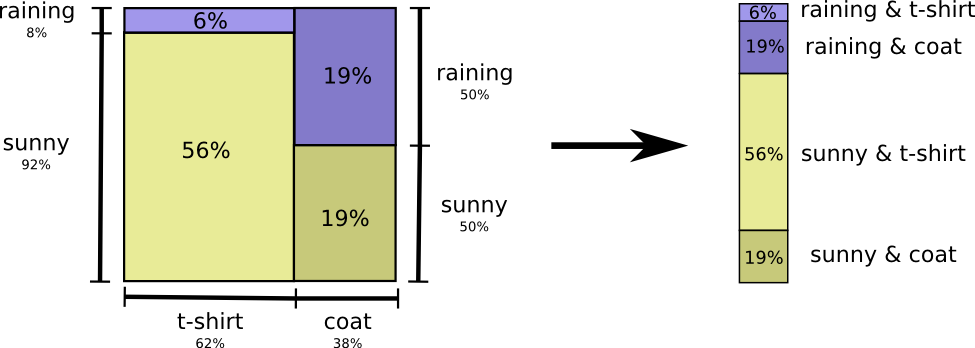
X和Y的联合熵,可以定义为:

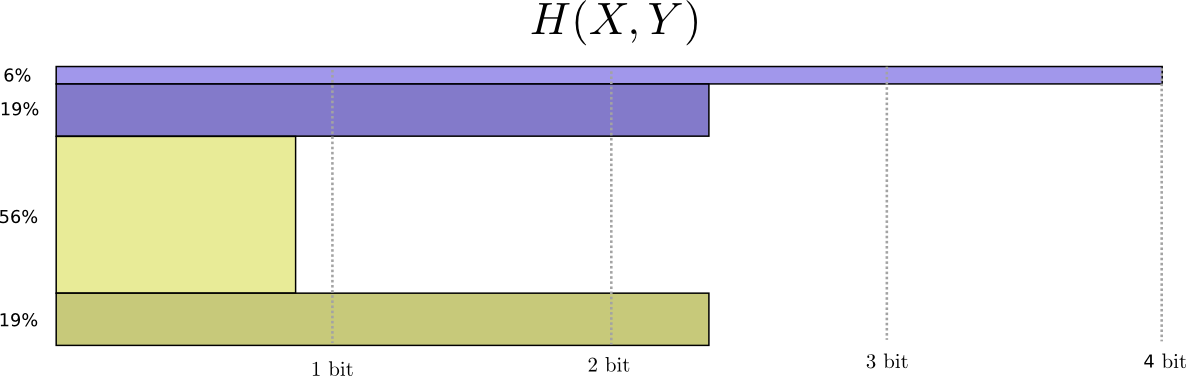
与前面的熵的定义是一样的,就是用两个变量代替了一个变量。将上面的图进行三维表示,如下:
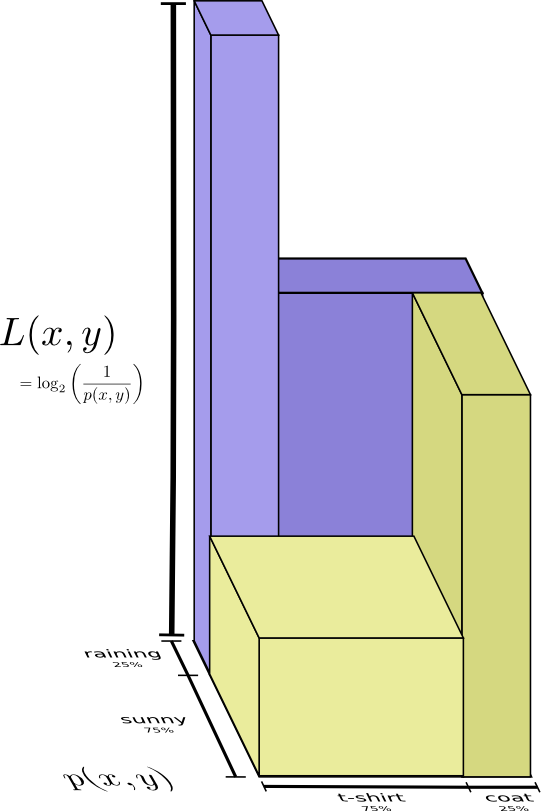
将晴天和雨天分开表示:
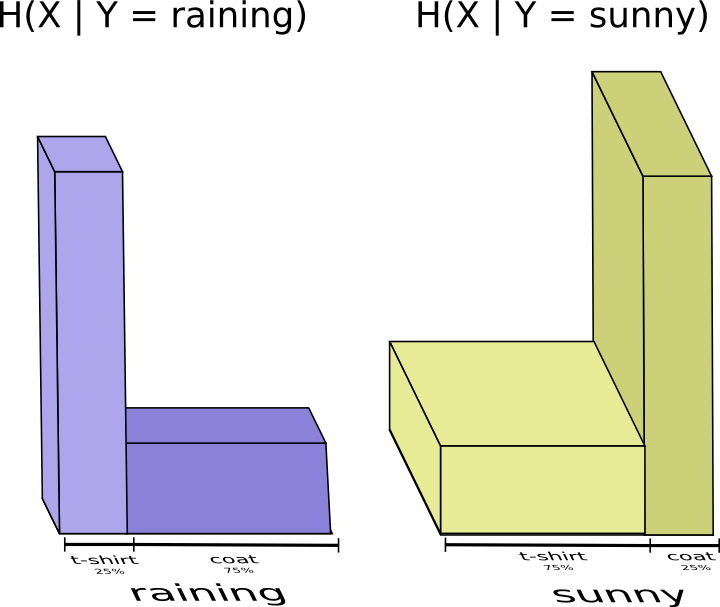
如果已知天气状况,由于天气已经对应该穿的衣服有一定的猜测,那么我就可以更加容易的选择所穿的衣服。如果天气晴朗,我就选择晴朗的最优编码,如果下雨,我用下雨的最优的编码,这两种情况,我都会比不知道天气更容易的判断我要穿什么。将两种情况放在一起,如下图所示:
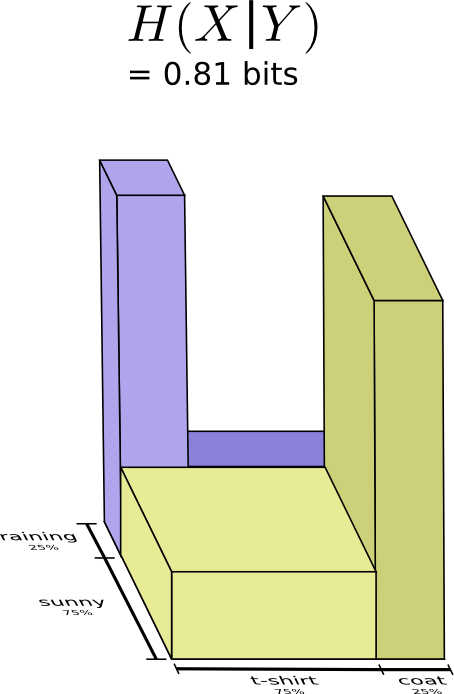
上面这种情况叫做条件熵,公式化可以表示为:

互信息
通过上面的例子,我们可以发现,已知一个变量意味着,我们可以使用更少的信息来对另外的变量进行交流。
假想信息量为一个长条,若两个事情之间有共享的信息,这些长条就重叠,表示如下:
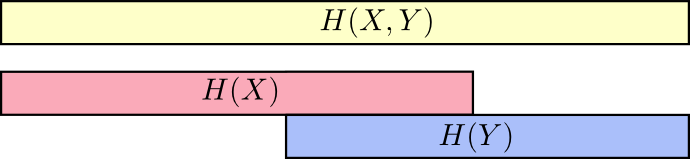
如图可以发现,所需的交流信息量分别在联合熵,边缘熵,条件熵三者递减。
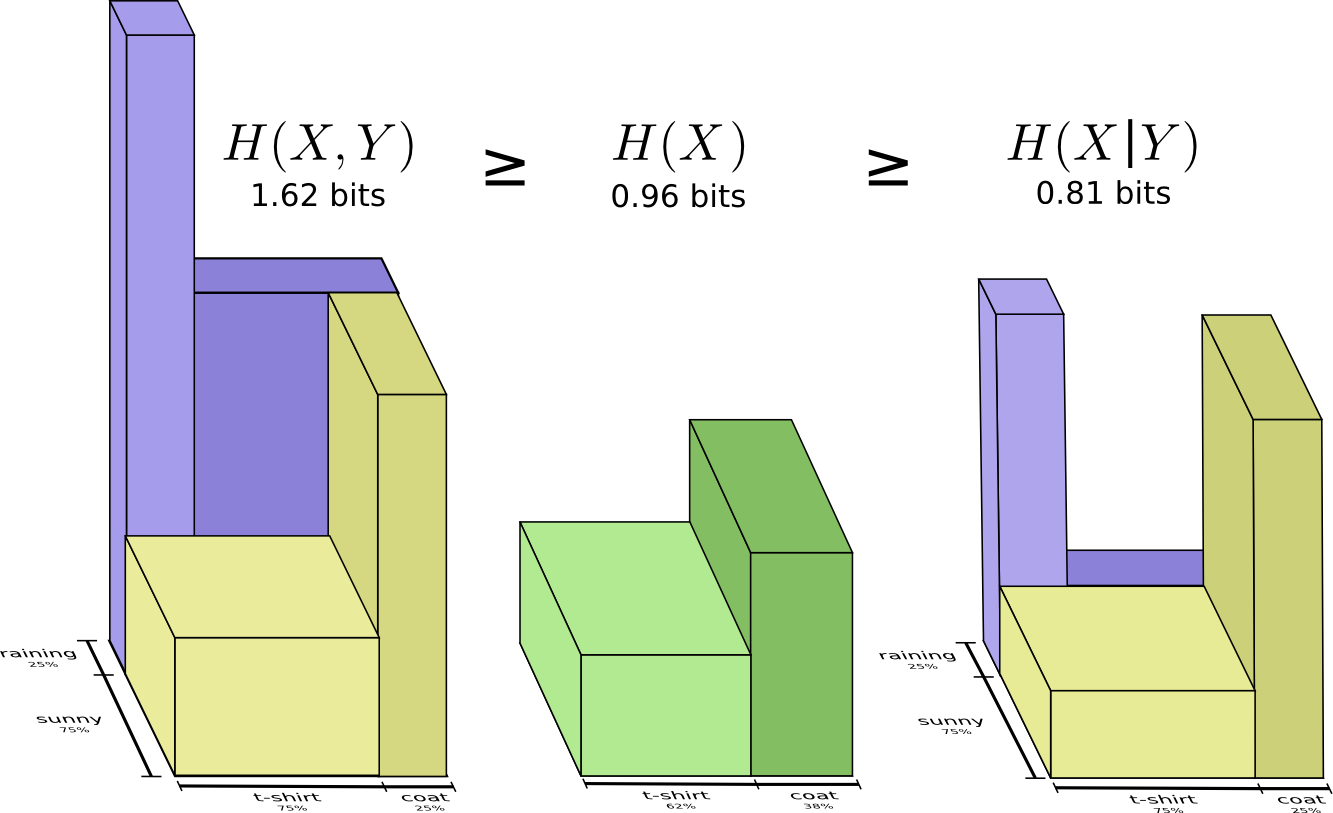
上面的图可能不够直观,可以通过长条的形式来表示,条件熵H(X|Y)指的是已知Y的情况下,如果俩人交流X,需要发送的信息量,即不在Y里面的X。下图中H(X,Y) >= H(X) >= H(X|Y)更显而易见些。
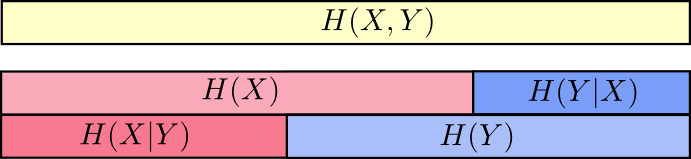
而且,也可以看出H(X,Y) = H(Y) + H(X|Y)
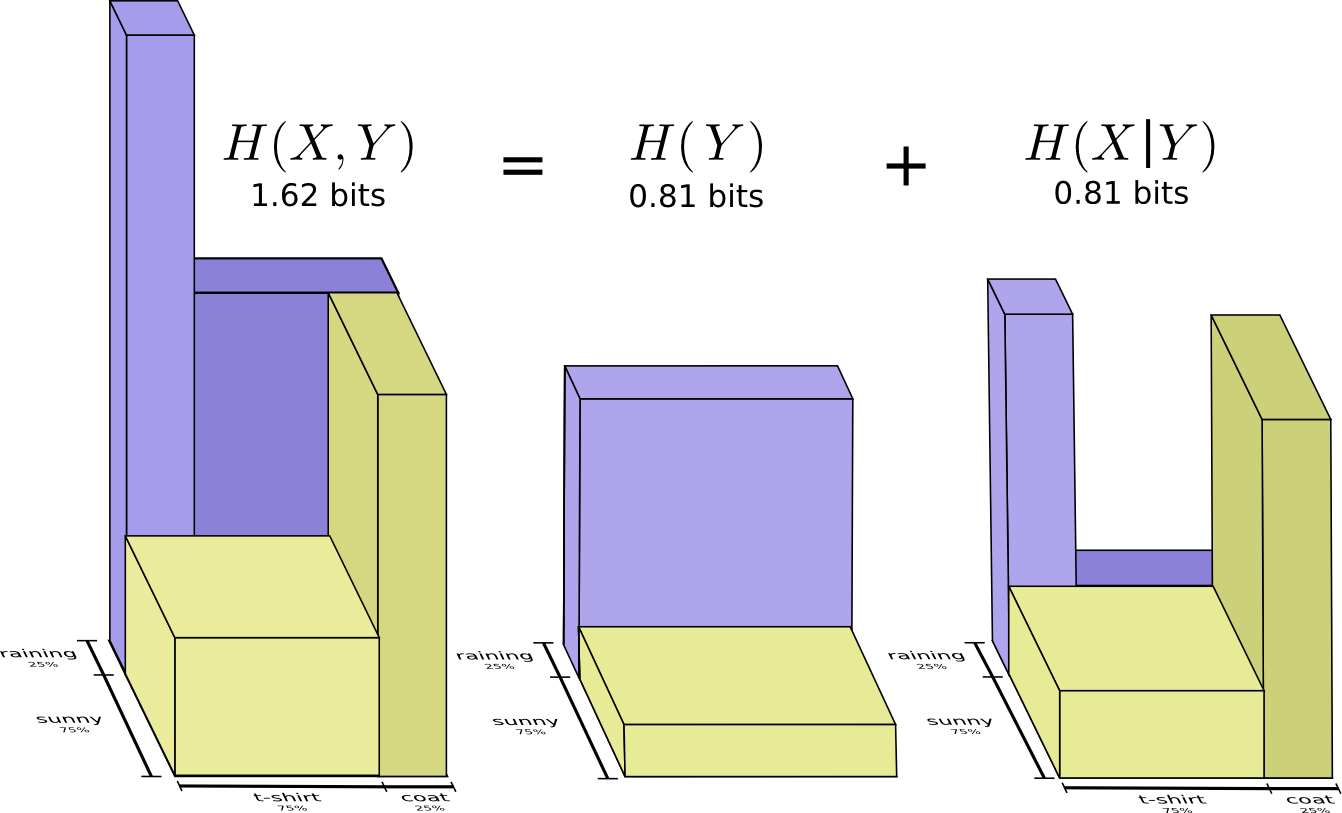
定义互信息I(X,Y),如下:

信息差是指:变量间不共享的信息,定义如下:

若已知一个变量,完全可以判断出另外的一个变量,那么信息差就为0,若二者更加相互独立,则信息差会增加。
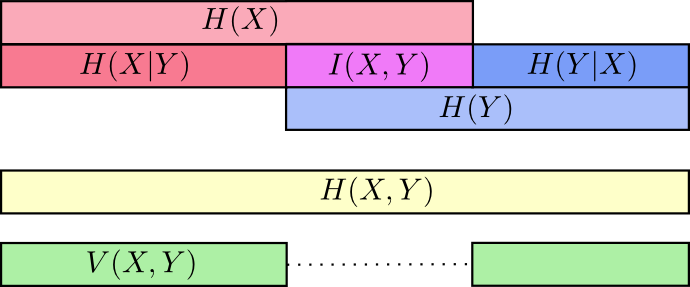
相对熵可以给出相同变量或变量集合的两个不同分布之间的距离,相对,信息差给出两个联合分布变量之间的距离。关于各种熵的解释,上图很清晰。
分数位
考虑一件事发生,可能有两种情况a,b,概率:a有71%的可能性发生,b有29%的可能性发生。
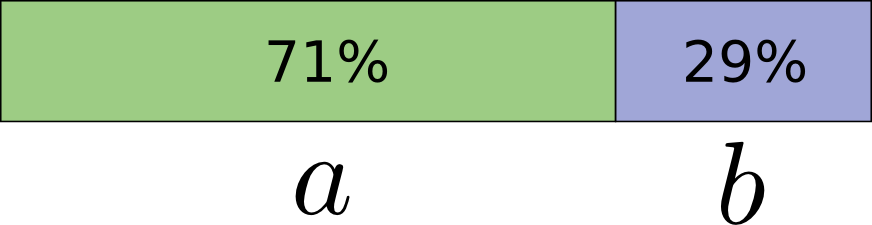
最优的编码:用0.5位表示a,用1.7倍表示b,如果你一次发送一个单词,好像不太可能,你不得不把它变成整数.但考虑如果一次发送几个信息:如果两件事情相互独立,分布相同,正常编码的话需要两位。但是更好的方法:
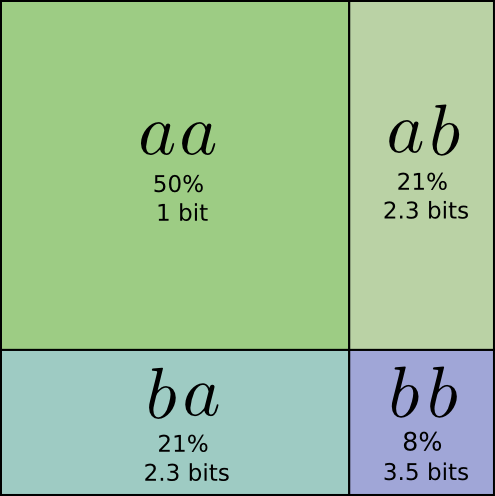
如果按照上面所说的分数位的编码格式,可以得到上面图示的概率分布表示,理想的分数位编码如下图:
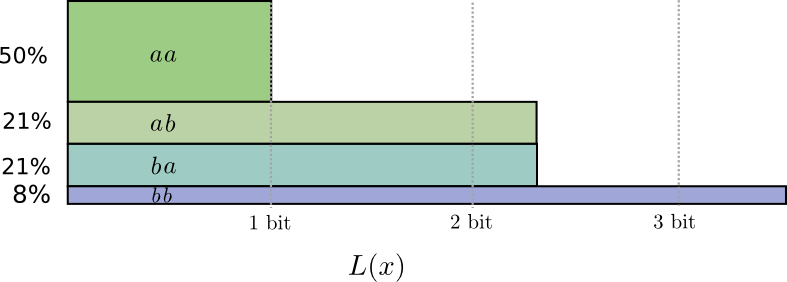
如果对码字长度取整,得到下面的情形:
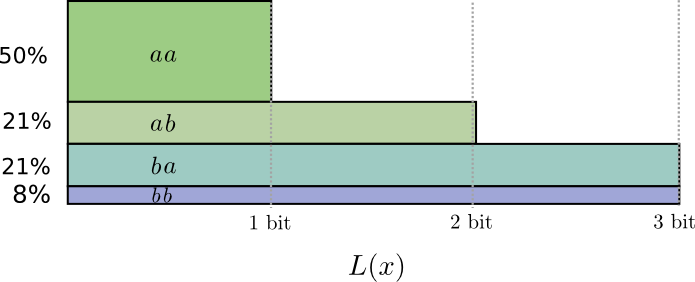
可以算出平均的编码长度为1.8.当事件的数目不断增加,每个码字的位数将会接近熵。
*http://https://en.wikipedia.org/wiki/Huffman_coding对分数位编码处理不是那么好,需要采取一些额外的策略
https://en.wikipedia.org/wiki/Arithmetic_coding可以渐进最优的处理分数位编码*
总结
量子理论可以用熵描述,许多统计力学和热力学的结果也可以用假设关于未知事物的最大熵来得到,赌博与相对熵有关。
信息理论给我们许多度量表达不确定性的方式:两个置信集合之间的差异,一个问题的答案与另一个问题之间关联性有多大,概率有多么弥散,概率分布之间的距离,两个变量之间的独立性有多强…
这篇关于信息熵(下)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!