【Python刷题Leetcode】动态规划（爬楼梯/打家劫舍/最大字段和/找零钱/三角形/最长上升子序列/最小路径和/地牢游戏）

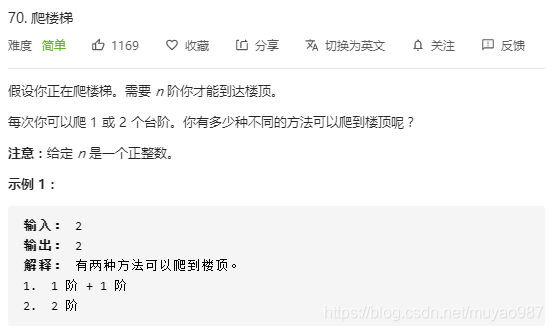
class Solution:# 递归法 超时了def climbStairs1(self, n: int) -> int:if n==1 or n==2:return n# 第1次爬1阶 共climbStairs1(n-1)；第1次爬2阶 共climbStairs1(n-2)；return self.climbStairs1(n-1)+self.climbStairs1(n-2)# 动态规划(dp)def climbStairs(self, n: int) -> int:dp = [0]*(n+3) # 最短是3个值 防止后面for循环越界dp[0],dp[1],dp[2]=0,1,2for i in range(3,n+1):dp[i]=dp[i-1]+dp[i-2]return dp[n]

class Solution:def rob(self, nums: List[int]) -> int:if len(nums)==0:return 0if len(nums)==1:return nums[0]if len(nums)==2:return max(nums[0],nums[1])# len(nums) >=3dp = [0]*(len(nums))dp[0],dp[1]=nums[0],max(nums[0],nums[1])for i in range(2,len(nums)):dp[i]=max(dp[i-1], dp[i-2]+nums[i])return dp[-1]

class Solution:def maxSubArray(self, nums: List[int]) -> int:dp = [0]*len(nums)dp[0] = nums[0]max_res = dp[0]for i in range(1, len(nums)):# 以nums[i]为结尾的结果dp[i]=max(dp[i-1]+nums[i], nums[i])if dp[i]>max_res:max_res = dp[i]return max_res

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# dp[i]是指的组成金额i所需的最少硬币数dp = [-1]*(amount+1)dp[0] = 0# 动态规划 从dp[1]开始递推for i in range(1,amount+1):# 内层循环coinsfor coin in coins:# 若i包含面值coin且i去掉coin后可达if i-coin>=0 and dp[i-coin]!=-1:# dp[i] = min(dp[i-1],dp[i-2],dp[i-5]) + 1 其中1 2 5是面值if dp[i]==-1 or dp[i-coin]+1<dp[i]:dp[i]=dp[i-coin]+1return dp[amount]

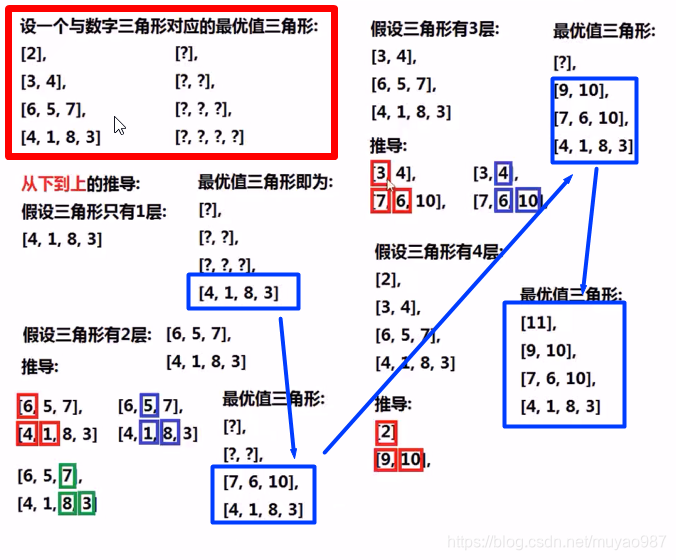
class Solution:def minimumTotal(self, triangle: List[List[int]]) -> int:if not triangle:return 0# triangle就是dp 最后一行不变 从倒数第二行往上递推for i in range(1,len(triangle)):line = len(triangle)-1-ifor j in range(len(triangle[line])):triangle[line][j]+=min(triangle[line+1][j],triangle[line+1][j+1])return triangle[0][0]

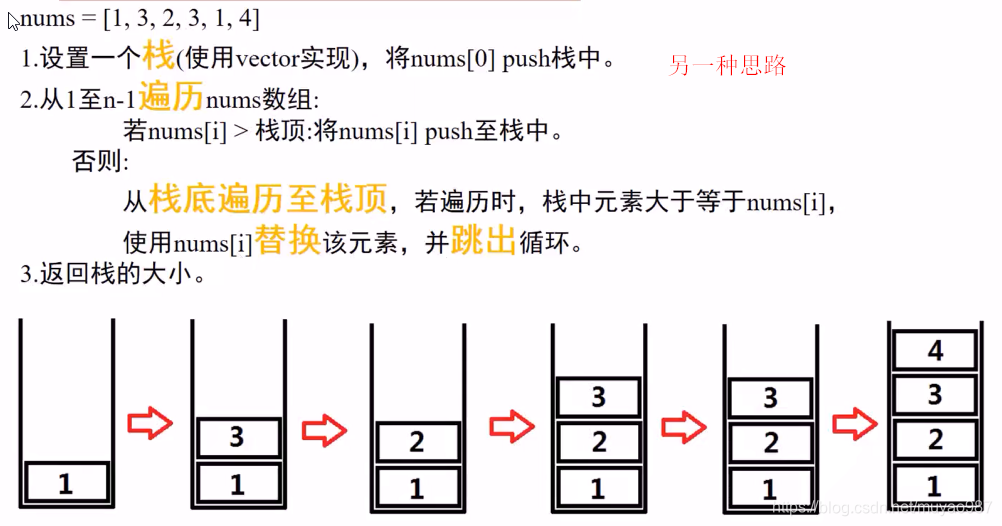
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:if len(nums)==0 or len(nums)==1:return len(nums)# dp[i]表示nums[i]为结尾的最长上升子序列长度 # dp[i+1] = max(dp[0],dp[1],..,dp[i])+1 其中max()里面对应的num都小于nums[i+1]dp = [1]*len(nums)res = 1for i in range(1, len(nums)):for j in range(0,i):if nums[i]>nums[j] and dp[j]+1>dp[i]:dp[i]=dp[j]+1if dp[i]>res:res=dp[i]return res

另一个算法：

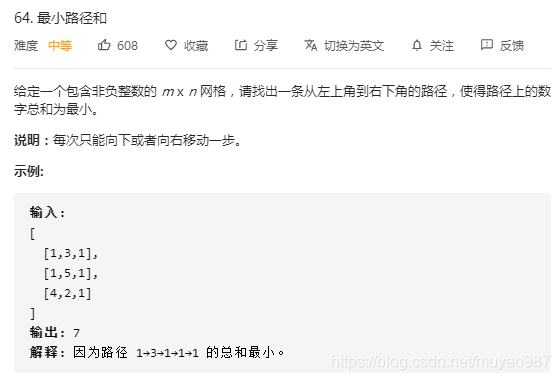
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:if not grid:return 0# 获取行和列m = len(grid)n = len(grid[0])# 初始化dp为全0 形状跟grid一样dp = []for i in range(m):tmp = []for j in range(n):tmp.append(0)dp.append(tmp)# 从左上到右下动态规划dp[0][0] = grid[0][0]# 初始化第0行for i in range(1,n):dp[0][i] = grid[0][i]+dp[0][i-1] # grid[0][i]只能从左边过来# 从第1行开始遍历for i in range(1,m):# 初始化第i行第0列dp[i][0] = grid[i][0]+dp[i-1][0]# 填其他列 要么从左边过来 要么从上边过来for j in range(1,n):dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]return dp[m-1][n-1]

class Solution:def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:if not dungeon:return 0# 获取行和列m = len(dungeon)n = len(dungeon[0])# 初始化dp为全0 形状跟dungeon一样dp = []for i in range(m):tmp = []for j in range(n):tmp.append(0)dp.append(tmp)# 初始化最后一个元素dp[m-1][n-1] = max(1, 1-dungeon[m-1][n-1])# 初始化最后一行0 ~ n-2 个元素for i in range(0,n-1):idx = n-2-idp[m-1][idx] = max(1, dp[m-1][idx+1]-dungeon[m-1][idx])# 初始化最后一列0 ~ m-2 个元素for i in range(0,m-1):idx = m-2-idp[idx][n-1] = max(1, dp[idx+1][n-1]-dungeon[idx][n-1])# print(dp)# 从倒数第2行开始往上遍历 遍历m-2 ~ 0 行, 每行遍历前n-2 ~ 0 列for i in range(0,m-1):row = m-2-ifor j in range(0,n-1):col = n-2-jprint(row,col)dp_min = min(dp[row+1][col],dp[row][col+1]) # 正下方 or 正右方dp[row][col]=max(1, dp_min-dungeon[row][col])# print(dp)return dp[0][0]