本文主要是介绍基于导数Zernike多项式拟合技术的干涉测量二维相位展开算法(原文翻译),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Zixin Zhao1,Hong Zhao1、Lu Zhang 1,Fen Gao2,Yuwei Qin3,Hubing Du
摘要:
我们提出了一种适用于一般干涉测量应用的相位展开方法。所提出的方法依赖于导数泽尼克多项式拟合(DZPF)技术,其中相位近似为泽尼克多项式的组合。然后使用最小二乘法来估计拟合系数。因此,相位展开问题被简化为这些系数的计算。由于采用了全场运算,因此该方法快速有效。此外,该方法直接提供所需相位,而无需进一步计算未对准误差。该方法结合了相位展开和波前拟合过程。仿真和实验结果验证了该方法的潜力。
关键词:相位展开算法,导数Zernike多项式拟合,干涉测量应用
1.引言
光学干涉仪可用于测量广泛的物理量。干涉仪提供的有趣数据中有条纹图案,它是由被测量的波前像差调制的相位的余弦函数。在分析这些干涉图的过程中,相位解调和相位展开都是必要的阶段。第一阶段通过相位测量算法[1]从原始干涉图中提取相位。通常,第一阶段导出的相位是包裹的,通常限制在-π到π的范围内。应使用相位展开器去除包裹相位中隐藏的不连续性。相位展开是相位提取过程中最具挑战性的最后一步。许多研究人员对此进行了探索,并提出了几种方法,如路径跟随方法[2-5]、最小二乘法[6-10]、区域法[11-13]或Regula。
在这里,我们主要讨论由Ghiglia等人[6]首次引入的最小二乘技术,将相位展开问题重新表述为离散泊松方程的解。已经提出了几种方法[9,10]来求解该方程。然后,梁[7]介绍了一种基于模型的相位展开方法。该方法通过截断泰勒级数和残差函数来表示解包裹的相位函数。即使它是为展开MR图像而设计的,它也应该同样适用于可以用低阶多项式近似的任何相位表面。之后,Arines[8]提出了一种使用正交多项式(如Zernike多项式)进行Shack–Hartmann检验的迭代最小二乘模态估计方法。这更适合于一般的干涉测量应用,但不能求解拟合过程中的第一个常数项。因此,引入了一个迭代过程。
在综合研究上述方法的基础上,本文提出了一种基于导数Zernike多项式拟合(DZPF)技术的高效非迭代相位展开算法。它本质上是一种最小二乘法,但工作速度更快,因为在展开过程中不需要迭代。该方法是在圆形条纹图案的背景下提出的,尽管它也适用于其他类型的条纹图案。本文的第二节介绍了该算法的原理。第3节和第4节分别介绍并讨论了将所提出的算法应用于展开模拟和真实相位图的结果
2.拟用方法说明
图1显示了新的相位展开方法的流程图。下面解释详细的代数公式。通常相位展开问题可以建模如下:
![]()
其中,(x ,y)是真相位,φ(x y)是包裹相位,k (x y)是要求解的整数。
对于一般的干涉测量测试,测量的相位总是可以分解为在单位圆中定义的一系列正交Zernike多项式[15]的总和,
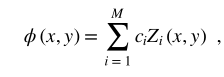
其中Z (x ,y)i是以极坐标书写的方程(3)中定义的第i个Zernike多项式,ci是相应的系数,M是要使用的多项式的数量,并且通常设置为等于36。
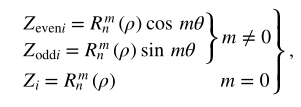
其中,i 是模式排序编号,而

其中指数n和m分别是径向度数和方位角频率,并且满足m≤= n ,(n− |m|)=even,偶数。M与n的关系为M=(n+1)/(n+2)(1)(2)/2。通过计算真实相位和包裹相位的一阶差,相位展开问题导致计算方程(2)中定义的系数=c i(i=1,2,3,...m)。因此,我们正在寻找的阶段将是使以下成本函数最小化的阶段,为了符号的简单性,省略了x,y依赖性,
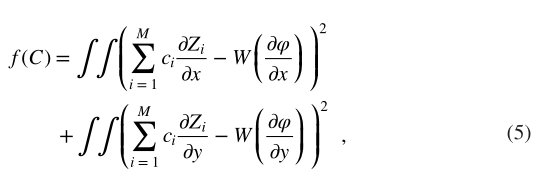
其中C=(c1,c2,c3...cM)是包含拟合系数的向量,W(·)是满足方程(6)的包裹算子。

计算成本函数的偏导数并将其设为零,就能得到如图所示的正态方程。将其设为零,我们就得到了如下所示的正则方程 式中:


图2:(a) 模拟条纹图案。(b) 以弧度表示的包裹相位。(c) 以弧度表示的展开相位。(d) 所提出方法的弧度残差。
其中,A是对方程(2)中定义的相位场进行一阶导数运算的矩阵,Δφ是包含x和y方向上的包裹相位差的向量,T是矩阵换位。显式表达式如下:

其中Z_(ix)和Z_(iy)是第i个Zernike多项式在x和y方向上的导数,W(·)是方程(6)中定义的包裹算子。k=1,2,....m -1,l=1,2,...n-1 其中 m ,n 分别是x方向和y方向上的像素数。
在最小二乘意义上求解正规方程,我们可以得到方程(10)左侧定义的估计相位_c(x ,y。


这篇关于基于导数Zernike多项式拟合技术的干涉测量二维相位展开算法(原文翻译)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








