MATLAB与Robotstudio建立socket通信（自我学习记续）中仿真模型的逆运动学和控制

1、前记：为了找到合适的逆解算法，作者不使用工具箱中的ikine函数或ikine6s，做数字书写的逆解，大致描述的推导如下

   2、逆运动学描述：已知，末端位姿---->(p,[n, o, a])  求解各关节角度配置---->q = [q1, q2,…qn] T  。

为了解决这个问题，通过运动解耦的过程求逆解。给出了逆运动学问题计算的最终方程如下：假设最终效应器的位置由变换矩阵给T，可以知道手腕的位置L 5的值（手腕和末端执行器之间的距离）通过以下表达式：

对应的第一关节等式：；其中A，B，t，β和K1为：

Li是图中所示的尺寸：

对应于关节2和3的方程是：

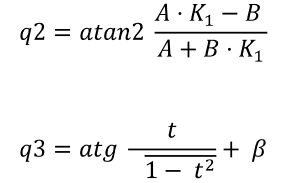
一旦知道关节（q1，q2，q3）的值并因此知道第一和第三关节（R03）之间的旋转，第三和第六关节之间的旋转（R36），则：   

一旦知道了所有数据，我们就可以轻松获得剩下的三个关节的值：

3、除了执行机器人的建模外，我们还将开发一种运动控制为我们的机器人手臂。运动控制尤其具有以下特征功能：
- 在笛卡尔空间的分析轨迹中转换程序中给出的运动规范。
- 对笛卡尔轨迹进行采样，获得所述轨迹的有限数量的点。
- 使用反向运动学，将每个点转换为对应的关节坐标（q1，q2，q3，q4，q5，q6）。
- 关节轨迹的采样以生成动态控制的参考。
- 获得的关节点的插值，为每个变量生成清晰的表达qi（t）传递或接近它们在后面的部分中，我们将观察如何执行三种可能的运动控制：
通过关节插补控制
笛卡尔插值控制
差分控制

4、创建数字面板。

    通过Matlab命令窗口请求的数字，机器人将在数字面板（工件坐标系）绘制出。面板的轮廓可以在页面末尾的图中看到。顶点（7,8,9,10,11,12），与面板所在的平面分开L / 10，允许工具远离面板移动到达新位置从中我可以继续追踪数字。

绘画时，工具将始终垂直于面板的平面（使用与系统{Sp}相同的方向。面板的位置不是唯一的，可以根据应用的要求进行修改。

接下来，将分析制作数字面板所需的Matlab代码。 前面斜体的％注释，解释了随附代码行的含义。

%绘制世界的参考系统
Origen=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
%数字面板的参考系，可以修改。 三种可能性：
PosPanel=transl(0.3,0,0.7)*TRi; %TRi是末端执行器在静止位置的正确旋转？
PosPanel=transl(0.5,0,0.2)*TRi*troty(pi/2); 
PosPanel=transl(0,0.5,0.6)*TRi*trotx(pi/2)*troty(pi/6) %我们的例子中，面板放置在XY平面上并平行于Z轴。
axis([-1 1 -1 1 -1 1]);hold on;grid on;
trplot(PosPanel,'color','r');
trplot(Origen);
%面板缩放
escala=0.1;
%面板参考系中各点的同构坐标。规范化
p1=escala*[0 0 0 1/escala]';
p2=escala*[0 1 0 1/escala]';
p3=escala*[1 1 0 1/escala]';
p4=escala*[2 1 0 1/escala]';
p5=escala*[2 0 0 1/escala]';
p6=escala*[1 0 0 1/escala]';
p7=escala*[0 0 -0.1 1/escala]';
p8=escala*[0 1 -0.1 1/escala]';
p9=escala*[1 1 -0.1 1/escala]';
p10=escala*[2 1 -0.1 1/escala]';
p11=escala*[2 0 -0.1 1/escala]';
p12=escala*[1 0 -0.1 1/escala]';
%总参考系中各点的坐标
p1T=PosPanel*p1;
p2T=PosPanel*p2;
p3T=PosPanel*p3;
p4T=PosPanel*p4;
p5T=PosPanel*p5;
p6T=PosPanel*p6;
p7T=PosPanel*p7;
p8T=PosPanel*p8;
p9T=PosPanel*p9;
p10T=PosPanel*p10;
p11T=PosPanel*p11;
p12T=PosPanel*p12;%绘制点
plot3([p1T(1) p2T(1) p3T(1) p4T(1) p5T(1) p6T(1) p7T(1) p8T(1) p9T(1) p10T(1)
p11T(1) p12T(1)],[p1T(2) p2T(2) p3T(2) p4T(2) p5T(2) p6T(2) p7T(2) p8T(2) p9T(2)
p10T(2) p11T(2) p12T(2)],[p1T(3) p2T(3) p3T(3) p4T(3) p5T(3) p6T(3) p7T(3) p8T(3)
p9T(3) p10T(3) p11T(3) p12T(3)],'go');
plot3([p1T(1) p2T(1) p3T(1) p4T(1) p5T(1) p6T(1) p1T(1)],[p1T(2) p2T(2) p3T(2)
p4T(2) p5T(2) p6T(2) p1T(2)],[p1T(3) p2T(3) p3T(3) p4T(3) p5T(3) p6T(3) p1T(3)],'r--');
plot3([p3T(1) p6T(1)],[p3T(2) p6T(2)],[p3T(3) p6T(3)],'r--');
%在数组中放置了每个顶点相对于全局解引用系统的完整位置。 
%第一步参考面板系，然后将点相应的转换应用于该参考系统中。
T_Vertices(:,:,1)=PosPanel*transl(p1(1:3));
T_Vertices(:,:,2)=PosPanel*transl(p2(1:3));
T_Vertices(:,:,3)=PosPanel*transl(p3(1:3));
T_Vertices(:,:,4)=PosPanel*transl(p4(1:3));
T_Vertices(:,:,5)=PosPanel*transl(p5(1:3));
T_Vertices(:,:,6)=PosPanel*transl(p6(1:3));
T_Vertices(:,:,7)=PosPanel*transl(p7(1:3));
T_Vertices(:,:,8)=PosPanel*transl(p8(1:3));
T_Vertices(:,:,9)=PosPanel*transl(p9(1:3));
T_Vertices(:,:,10)=PosPanel*transl(p10(1:3));
T_Vertices(:,:,11)=PosPanel*transl(p11(1:3));
T_Vertices(:,:,12)=PosPanel*transl(p12(1:3));
%现在执行数字的定义。 
cero=[1 2 3 4 5 6 1 7];%0
uno=[1 6 5 11 12 7];%1
dos=[8 2 1 6 3 4 5 11 12 7];%2
tres=[8 2 1 6 5 4 10 9 3 6 12 7];%3
cuatro=[8 2 3 6 12 7 1 6 5 11 12 7];%4
cinco=[1 2 3 6 5 4 10 9 8 7];%5
seis=[1 2 3 4 5 6 3 9 12 7];%6
siete=[8 2 1 6 5 11 12 7];%7
ocho=[1 2 3 4 5 6 1 7 12 6 3 9 12 7];%8
nueve=[12 11 5 6 1 2 3 6 12 7];%9
%将机器人放在位置7，这将是休息的位置？？？
qreposo=irb120_ikine(T_Vertices(:,:,7),[0 0 0 0 0 0]);
irb120.plot(qreposo);

机器人和数字面板：

4.1、使用Matlab绘制数字--笛卡尔轨迹。

      为了开发我们的最终数字绘图应用程序，我们可以提出两种可能的解决方案：通过关节轨迹或通过笛卡尔轨迹。通过关节轨迹的解决方案意味着必须将每个顶点的关节配置，和关节配置对应于顶点之间的点通过socket发送到机器人。考虑传送的时间和便捷-------选择笛卡尔轨迹来实现。

4.2、使用Matlab中的机器人模型获得的结果。

      我们需要通过笛卡尔轨迹来执行本节的解决方案。使用三个文件，其中两个在上面提到“创建数字面板”，文件mdl_irb120和文件panel_numeros。 因此，我们专注于对第三个文件的分析aplicación_ikine。
在这个文件中，我们将通过a的路径跟踪数字顶点到另一个。 我们将计算下一个顶点，然后我们将计算10个点在每个顶点之间进行插值，以实现顶点之间的轨迹最大笔直，尽可能准确。以下代码：

%从顶点到顶点
n=length(num);
q0=qreposo;
%首先，从静止位置到第一个要绘制的顶点
T1=T_Vertices(:,:,7);
T2=T_Vertices(:,:,num(1));
Ts=ctraj(T1,T2,10); %这每个路径部分选择10个点，10个插值
qs=irb120_ikine(Ts,q0);
q0=qs(end,:);
irb120.plot(qs);
for i=1:(n-1)
T1=T_Vertices(:,:,num(i));
T2=T_Vertices(:,:,num(i+1));
Ts=ctraj(T1,T2,10); % 每个路径部分再次有10个点
qs=irb120_ikine(Ts,q0);
q0=qs(end,:);
irb120.plot(qs);
end

     首先，将机器人置于静止位置，等待用户接收你要画的数字。当给出这个顺序时，机器人通过我们之前分析过的代码进行计算
它必须去的下一个顶点（依次计算10个中间点制作更准确的轨迹）。在这些计算之后，机器人移动到下一个顶点，依此类推。我们将观察到机器人与面板分离（我们在4.3节中讨论过）“创建数字面板”）以避免在已经制作的线上绘画。

4.3、机器人使用irb120类获得的结果。

      我们只是在Matlab中看到应用程序的解决方案，必要时使用套接字或先前创建的接口完成数据发送给RS。因此，为了演示套接字和接口的功能，我们继续首先检查使用RobotStudio模拟器创建的程序，然后将其加载到IRC5控制器上以查看真实机器人的结果。下面介绍的版本有一系列变体，我们刚刚在Matlab中进行了分析。例如，我们需要通过服务器实现连接部分。我们已经研究过的TCP / IP功能。它也会改变你发送数据到机器人的方式。我们将使用我们在前面部分中创建的类“irb120”发送给机器人中的每一个点和位置都是用我们开发的机器人模型计算出来的。接下来，我们将看到与我们刚刚版本相关的代码包括：

% 我们通过类irb120与机器人连接
robot.connect;
%首先，我们从静止位置到第一个顶点
T2=T_Vertices(:,:,num(1));
pos=transl(T2);
% 毫米进给
pos=pos*1000;
rot=tr2rpy(T2);
% 度--弧度
rot=rot*180/pi;
robot.TCProtandpos([rot(3) rot(2) rot(1) pos(1) pos(2) pos(3)]);
pause(2);
% 从顶点到顶点
n=length(num);
q0=qreposo;
for i=1:(n-1)
T2=T_Vertices(:,:,num(i+1));
pos=transl(T2);
%
pos=pos*1000;
rot=tr2rpy(T2);
% 
rot=rot*180/pi ;
robot.TCProtandpos([rot(3) rot(2) rot(1) pos(1) pos(2) pos(3)]);
pause(2);
end

论文中的演示：

4.4、通过差分控制绘制数字
现在我们将采用第二种方式来执行数字轨迹的绘制，而不是使用irb120类。我们将使用我们创建的Simulink块，调用“Irb120”。在本节中，我们将使用Simulink工具和.m文件以及从Matlab命令窗口输入的命令。

在为最终应用程序实现此解决方案之前，我们必须引出某些必要的概念，以便理解我们将会看到下方内容。差分控制利用逆雅可比矩阵来计算达到一定速度所需的关节速度（或笛卡尔轨迹速度--末端执行器速度），根据已知的关系：

这种控制方法的最大优点是它不需要运动学的逆。（更多的自由度数而不是任务空间中的维度），因为受到牵制（较少的程度自由而不是任务空间的维度）。差分控制方案离散方程响应，以下：

其中第二个等式是允许计算变量的积分器从当前向量和下一个采样周期末端执行器所需的速度ѵ。该算法可以在开环和闭环中实现。我们已经实现了闭环算法。 在Simulink文件中我们将在下面看到，我们还包括我们的irb120模块块，其中将向机器人发送通过计算的点和位置组成差分控制模型的一组块的执行。具有块“irb120”的差分控制的Simulink模型

     如前所述，我们将看到Matlab中的操作演示，模拟机器人、真实机器人的演示。要实现此应用程序，我们需要使用另外两个文件， 上图中看到的Simulink模型以及一个名为genera_Ts_num.m（左下角）文件的代码可以在下面看到（代码用于连接RobotStudio，稍后看到的演示只来自Matlab平台）：

%打开连接以执行与机器人的通信
global t
t=tcpip('127.0.0.1',1024);
fopen(t);
numero=input('Enter the number to be painted: ');
switch (numero)
case 0num=cero;
case 1num=uno;
case 2num=dos;
case 3num=tres;
case 4num=cuatro;
case 5num=cinco;
case 6num=seis; 
case 7num=siete;
case 8     num=ocho;
case 9
num=nueve;otherwise
error('Unvalid Entry');
end
%初始化结构的字段，为空
Ts_num.time=[];
Ts_num.signals.values=[];
Ts_num.signals.dimensions=[4 4];
% 从点到点
n=length(num);
q0=qreposo;
for i=1:(n-1)
T1=T_Vertices(:,:,num(i));
T2=T_Vertices(:,:,num(i+1));
%每个路径部分有10个点
Ts=ctraj(T1,T2,20);
Ts_num.signals.values(:,:,[length(Ts_num.signals.values)+1:length(Ts_num.signals.values)+length(Ts)])=Ts;
end
%每100毫秒产生一次矢量
paso=2; %一步一步
Ts_num.time=[0:paso:(length(Ts_num.signals.values)-1)*paso];
%仿真完成
Tstop=Ts_num.time(end);

     执行此应用程序的方式与其他应用程序类似，但不包括执行Simulink文件。然后，我们有文件mdl_irb120，panel_numeros，（看看它是怎么回事绘制数字），genera_Ts_num和差分控制文件.mdl。为了更好地显示结果，我们在Matlab中创建了一个图形
面板模式，更好地观察数字的绘制。我们将在下面的图中看到数字8（最复杂）的布局，通过Simulink模块irb120和差分控制。

绘制的数字‘8’。

     在通过Matlab进行的模拟中，一眼就看不到任何问题执行数字的绘制，但通过发送irb120块结果和当机器人处理它们时，他所做的绘画并不像我们所能做的那样精确见前面的图片。在下一节中，我们将使用块“irb120”显示解决方案我们将分析出现问题的原因。

4.5、使用Simulink块“Irb120”获得机器人的结果

      本节使用的代码和文件是上面提到的那些。它在Matlab中解决方案的唯一区别是引入RobotStudio模拟器以及如何运行程序。
在下面的图像中，观察应用程序在机器人模拟器中运行情况，依次显示在Matlab中制作的窗口（图）检查路径是否同时发生，注意观察绘制的数字0在俩者中区别。

    上面提到的问题来源于运动学的计算问题，即; 差分控制涉及我们不要求直线路径的问题。 如果我们观察zetas，它们不是零（假设我们将面板放在Z = 0的平面中）它们会变化，所以计算出的q被发送到机器人并且结果是正确的数字图，因为它被理解为是数字 ，但它不精确，也没有线性轨迹。由于socket的时间有限（大约三秒钟），我们无法对真实机器人进行测试，因为机器人在短时间内收到太多订单而没有时间执行每一个订单， 所以数字绘制没有正确完成。

实体测试：

5、论文的结论和未来工作（通常看论文都会关注这一点）

         在这个项目中，已经开发了几种可行的Socket通信接口，实现从Matlab控制ABB机器人手臂IRB120。通过GUI可以很好地完成，Matlab类，或Simulink模块。有几个延伸选项可以在Matlab中实现应用程序，在一定条件范围下控制机器人。在通信中检测到的主要限制是套接字（socket）需要向机器人发送数据包的时间，大约3秒钟。所以在一定程度上可以开发的Matlab类型的应用程序。

        简而言之，开发控制的应用程序将是合适的在笛卡尔空间的层面，即发送工具的目标点位信息，但是需要更精确关节配置（逆解算法）来实现。这不会限制大多数人，因为低级控制算法已经实现了，机器人控制器一旦建立了通信接口，就可以将其作为用于控制机器人手臂的多种应用程序（MATLAB开发），如可以避免相机检测到的路径中的障碍物，通过Kinect检测到的人体手臂运动的再现，检测和堆叠工作站内的某些物体等。

后记：翻译大致如上了！因为确实Robotstudio中的交互程序（接受的数据如何转换为工具坐标并使机器人运动，单轴运动如何实现。。。）、、、再研究吧。如果实现了，后续再贴出！