本文主要是介绍[机器学习与scikit-learn-25]:算法-聚类-KMeans的适用范围与评估指标,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123459216
目录
前言:
第1章 KMeans的适合与不适合场景
1.1 KMeans的本质与适用场景
1.2 KMeans的不适用场合
1.3 不适合场合下的错误聚类
第2章 KMeans效果评估面临的问题
2.1 概述
2.2 KMeans的Inertia指标面临的问题
第3章 KMeans效果评估的方法
3.1 当真实标签已知的时候
3.2 当真实标签未知的时候:基本思想
3.3 当真实标签未知的时候:轮廓系数
3.4 轮廓系数的代码演示
3.5 当真实标签未知的时候:Calinski-Harabaz Index
3.6 卡林斯基-哈拉巴斯指数代码示例
3.7 上述两个指标运行时间比较
前言:
在KMeans的代码使用示例中,我们看出所有点到质心的距离Inertia指标,并不能作为评估模型好坏的指标。且有标签样本的分类评估指标也不适合聚类,因为聚类没有参考标签可以比较。
第1章 KMeans的适合与不适合场景
1.1 KMeans的本质与适用场景
 KMeans的本质是找“质心”的过程,质心是族类样本的均值中心。
KMeans的本质是找“质心”的过程,质心是族类样本的均值中心。
这就意味着,KMeans的前提条件,样本数据必须:
(1)按照族的方式分布
(2)有质心存在,有中心点存在
(3)族之间不能重叠
上述的前提条件,用数学的术语描述就是:
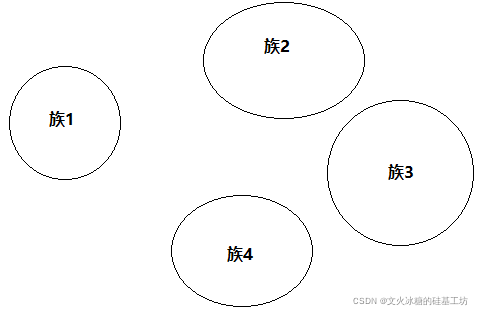
每个族,实际本质上是一个圆,圆心就族心或质心,使用Kmeans的条件是:
(1)圆与圆直接不相交
(2)圆与圆直接不包含
1.2 KMeans的不适用场合
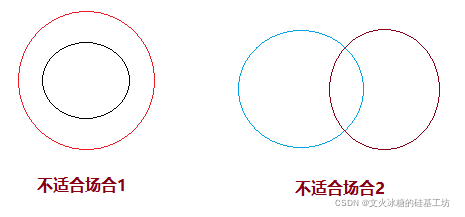
1.3 不适合场合下的错误聚类
 上述图形中,除了第5幅图是符合聚类,其他都不适合采用聚类算法。
上述图形中,除了第5幅图是符合聚类,其他都不适合采用聚类算法。
这就需要一种指标来衡量KMeans距离效果的好坏。
第2章 KMeans效果评估面临的问题
2.1 概述
不同于分类模型和回归,聚类算法找质心的原理非常简单,步骤也非常方便,然而模型评估不是一件简单的事。
在分类中,有直接结果(标签)的输出,并且分类的结果有正误之分,所以我们使用预测的准确度,混淆矩阵,ROC曲线等等指标来进行评估,但无论如何评估,都是在”模型找到正确答案“的能力。
在回归中,由于要拟合数据,我们有SSE均方误差,有损失函数来衡量模型的拟合程度。但这些衡量指标都不适合于聚类。
聚类模型的结果不是某种标签输出,并且聚类的结果是不确定的,其优劣由业务需求或者算法需求来决定,并且没有永远的正确答案。那我们如何衡量聚类的效果呢?
2.2 KMeans的Inertia指标面临的问题
KMeans的目标是确保“簇内差异小,簇外差异大”,可以通过衡量簇内差异来衡量聚类的效
果。
Inertia是用距离来衡量簇内差异的指标,是否可以使用Inertia来作为聚类的衡量指标呢?即使得Inertia越小模型越好呢?
不行,这个指标的缺点太大:
(1)首先,它不是有界的。
我们只知道,Inertia是越小越好,是0最好,但我们不知道,一个较小的Inertia究竟有没有
达到模型的极限,能否继续提高。
(2)第二,它的计算太容易受到特征数目的影响
数据维度很大的时候,Inertia的计算量会陷入维度诅咒之中,计算量会爆炸,不适合用来一次次评估模型。
(3)第三,它会受到超参数K的影响
在我们之前的常识中其实我们已经发现,随着K越大,Inertia注定会越来越小,但这并不代表模型的效果越来越好了。当K=样本数据的时候,每个点都是一个质心,即Inertia=0, 很显然,这时候的模型其实不是最好的。
(4)第四,Inertia对数据的分布有假设,
它假设数据满足凸分布(即数据在二维平面图像上看起来是一个凸函数的样子),并且它假设数据是各向同性的(isotropic),即是说数据的属性在不同方向上代表着相同的含义。但是现实中的数据往往不是这样。所以使用Inertia作为评估指标,会让聚类算法在一些细长簇,环形簇,或者不规则形状的流形时表现不佳。
第3章 KMeans效果评估的方法
3.1 当真实标签已知的时候
虽然我们在聚类中不输入真实标签,但这不代表我们拥有的数据中一定不具有真实标签,或者一定没有任何参考信息。当然,在现实中,拥有真实标签的情况非常少见(几乎是不可能的)。
但如果拥有真实标签,我们更倾向于使用分类算法。
但不排除我们依然可能使用聚类算法的可能性。如果我们有样本真实聚类情况的数据,我们可以对于聚类算法的结果和真实结果来衡量聚类的效果。常用的有以下三种方法:

三种方法的原理不用,但在使用方法确实一致的:就是用输入样本的标签与预测值进行比较。
- 输入样本的标签值
- 模型的预测值
由于带标签的情况,往往采用分类算法,而不是聚类算法,因此这种情形不多探讨。
3.2 当真实标签未知的时候:基本思想
在99%的情况下,我们是对没有真实标签的数据进行探索,也就是对不知道真正答案的数据进行聚类。这样的聚类,基本的评估思想是:
(1)簇内的稠密程度(簇内差异小)
(2)簇间的离散程度(簇外差异大)
现在就要找到合适的算法,来计算簇内的稠密程度和簇间的离散程度。
3.3 当真实标签未知的时候:轮廓系数
轮廓系数是最常用的聚类算法的评价指标。
它是对每个样本来定义的,它能够同时衡量:
1)样本与其自身所在的簇中的其他所有样本的相似度a(相似度用距离来表达),等于样本与同一簇中所有其他点之间的平均距离
2)样本与其他簇中的所有样本的相似度b(相似度用距离来表达),等于样本与下一个最近的簇中的所有点之间的平均距离。
根据聚类的要求”簇内差异小,簇外差异大“,我们希望:
- b永远大于a,
- 并且大得越多越好。

轮廓系数范围是(-1,1)
(1)好:s值越接近1,表示样本与自己所在的簇中的样本相似好,并且与其他簇中的样本不相似
(2)差:当样本点与簇外的样本更相似的时候,轮廓系数就为负。这些样本点在其族内就是属于异类。
(3)同族:当轮廓系数为0时,则代表两个簇中的这些样本的相似度一致,两个簇本应该是一个簇。
可以总结为轮廓系数越接近于1越好,负数则表示聚类效果非常差。
如果一个簇中的大多数样本具有比较高的轮廓系数,则簇会有较高的总轮廓系数,则整个数据集的平均轮廓系数越高,则聚类是合适的。
如果大量的样本点具有低轮廓系数甚至负值,则聚类是不合适的,聚类的超参数K可能设定得太大或者太小。
轮廓系数的表达方式:
(1)轮廓系数的所有样本的均值
在sklearn中,我们使用模块metrics中的类silhouette_score来计算轮廓系数,它返回的是一个数据集中,所有样本的轮廓系数的均值。
(2)轮廓系数的单样本的实际值
我们还有同在metrics模块中的silhouette_sample,它的参数与轮廓系数一致,但返回的是数据集中每个样本自己的轮廓系数。
3.4 轮廓系数的代码演示
from sklearn.metrics import silhouette_score
from sklearn.metrics import silhouette_samples# X: 每个实际样本的向量值
# y_pred:每个样本的分类预测值
y_pred = cluster.fit_predict(X)
print("X.shape", X.shape)
print("y_pred", y_pred.shape)
print("y_pred", y_pred[0:12])score = silhouette_score(X, y_pred)
print("平均轮廓分数:",score)samples = silhouette_samples(X,y_pred)
print("单样本的轮廓分数:\n", samples[0:12])X.shape (500, 2)
y_pred (500,)
y_pred [2 2 3 1 0 1 0 0 0 0 2 2]
平均轮廓分数: 0.6505186632729437
单样本的轮廓分数:[0.62903385 0.43289576 0.55834047 0.82660742 0.35213124 0.741232520.68902347 0.58705868 0.04062548 0.73241492 0.59363669 0.75135825]
轮廓系数有很多优点:
- 它在有限空间中取值,使得我们对模型的聚类效果有一个“参考”。
- 并且,轮廓系数对数据的分布没有假设,因此在很多数据集上都表现良好。
- 它在每个簇的分割比较清洗时表现最好。
轮廓系数也有缺陷
它在凸型的类上表现会虚高,比如基于密度进行的聚类,或通过DBSCAN获得的聚类结果,如果使用轮廓系数来衡量,则会表现出比真实聚类效果更高的分数。
3.5 当真实标签未知的时候:Calinski-Harabaz Index
除了轮廓系数是最常用的,我们还有卡林斯基-哈拉巴斯指数(Calinski-Harabaz Index,简称CHI,也被称为方差比标准),戴维斯-布尔丁指数(Davies-Bouldin)以及权变矩阵(Contingency Matrix)可以使用。
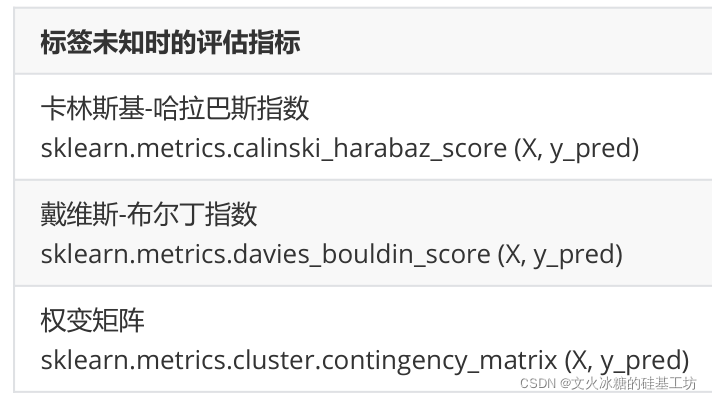
在这里我们重点来了解一下卡林斯基-哈拉巴斯指数。
Calinski-Harabaz指数越高越好。
对于有k个簇的聚类而言,Calinski-Harabaz指数s(k)写作如下公式:
![]()

3.6 卡林斯基-哈拉巴斯指数代码示例
from sklearn.metrics import calinski_harabasz_score# X: 每个实际样本的向量值
# y_pred:每个样本的分类预测值
y_pred = cluster.fit_predict(X)
calinski_harabasz_score(X, y_pred)2704.4858735121097
卡林斯基-哈拉巴斯指数是没有边界的指数,该值越大越高。
3.7 上述两个指标运行时间比较
from time import time
t0 = time()
calinski_harabasz_score(X, y_pred)
print(time() - t0)t0 = time()
silhouette_score(X,y_pred)
print(time() - t0)0.0 0.005000114440917969
轮廓系数虽然在[-1,1]之间,是有界指标,直观,但耗时也是比较大的。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123459216
这篇关于[机器学习与scikit-learn-25]:算法-聚类-KMeans的适用范围与评估指标的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





