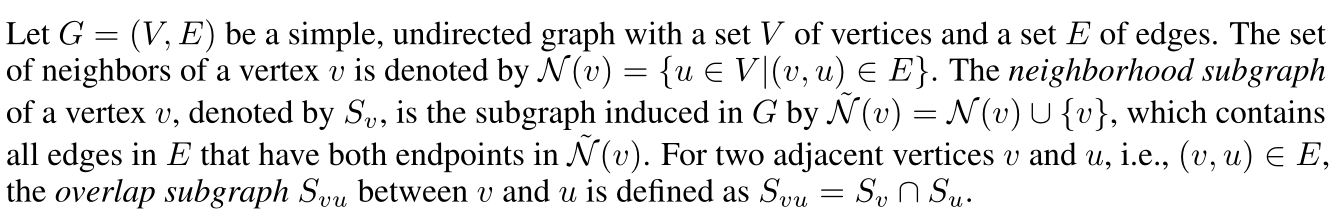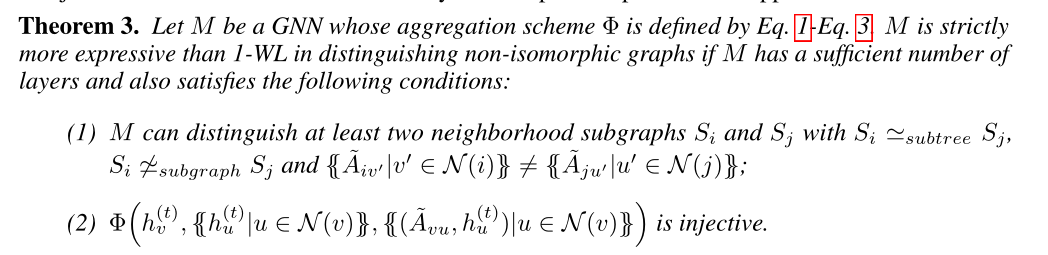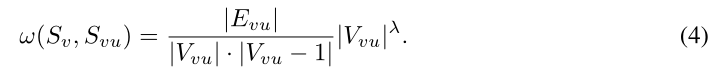表现力超过GIN和WL同构检验的GNN：A NEWPERSPECTIVE ON “HOW GRAPH NEURAL NETWORKS GO BEYOND WEISFEILER-LEHMAN?“

论文和代码，代码在补充材料中： A New Perspective on "How Graph Neural Networks Go Beyond Weisfeiler-Lehman?" | OpenReview

ICLR 2022的高分论文，共4个评委，全8分

内容：提出了一种新的消息聚合框架，可以超过GIN，达到比WL同构检验更好的表达能力，并给出了该框架下的一个实例：GraghSNN

1 三种局部同构的层次

两个定义

• 邻居子图：即一个节点的邻居+自己，和所有以邻居+自己为端点的边
• 重叠子图：即两个相邻节点邻居子图的交集
• 相关严谨的定义（懒癌不想打公式了）
  • 

• 
  • 上图清晰地标明了邻居子图和重叠子图
  • 邻居子图的节点：自己加一阶邻居，边：节点间的所有边 ，如上图G1的V（可以视为任何一个节点），它的邻居子图就是自己的加邻居，然后再加上这些节点再原图中对应的边
  • 重叠子图：两节点的邻居子图的交集，比如说G1的V和V1间的重叠子图，就是V的邻居子图和V1的邻居子图的交集

三种层次的同构

• 
  • 分别为子图同构，重叠同构，和子树同构。三者的关系是，若两个图为子图同构，则，必为重叠同构；若为重叠同构，则必为子树同构，反之都不然
  • 
    • 左图中两个节点𝑆𝑖,𝑆𝑗是重叠同构的，右图是子树同构的。注意，此时的三种重构，指的是节点间的，而不是图间的

2 通用消息传递框架

• G中所有的重叠子图
  • 
• 结构系数（每一个节点与其邻居之间的）
  • 
  • 需满足以下三个条件：局部封闭性（对完全图，节点越多A越大）、局部稠密行（节点相同，边越多的A越大）、同构不变性（同构图的A值相同）
    • 

• 框架的具体内容（{{}}表示多集，~表示A已经被归一化）
  • 
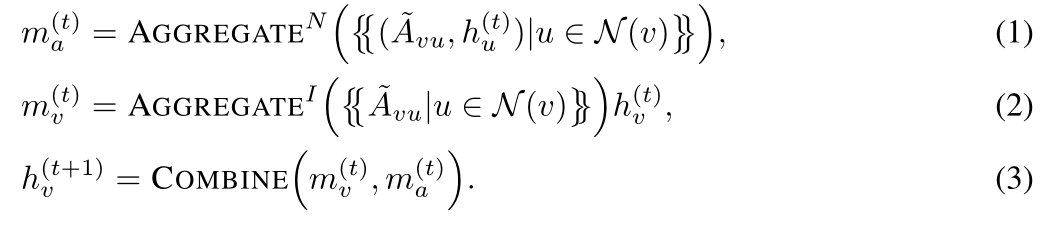
  • 可以类比一下，聚合操作中的N表示节点邻居聚合，I表示节点的更新

• 消息传递框架比1-WL更有效的条件（可以区分 子树同构而子图不同构的节点，单射）:
  • 

3 GraghSNN

• 具体实现
  • 
• 特征更新
  • 
• GraphSNN由于再原来的基础上加入了结构系数，因而比一般的GIN和1-WL更具有表达能力，相关的三条定理
  • 
• 所有的证明都在附录中

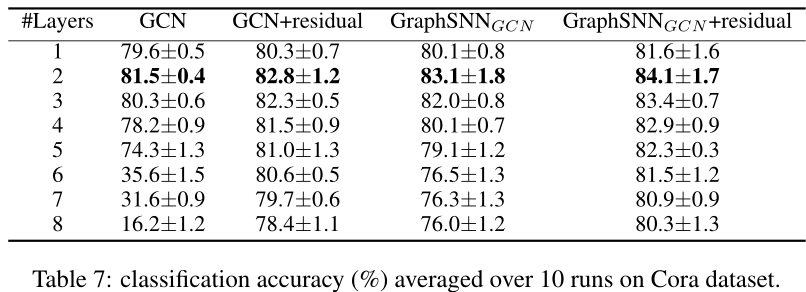
4 实验

对比

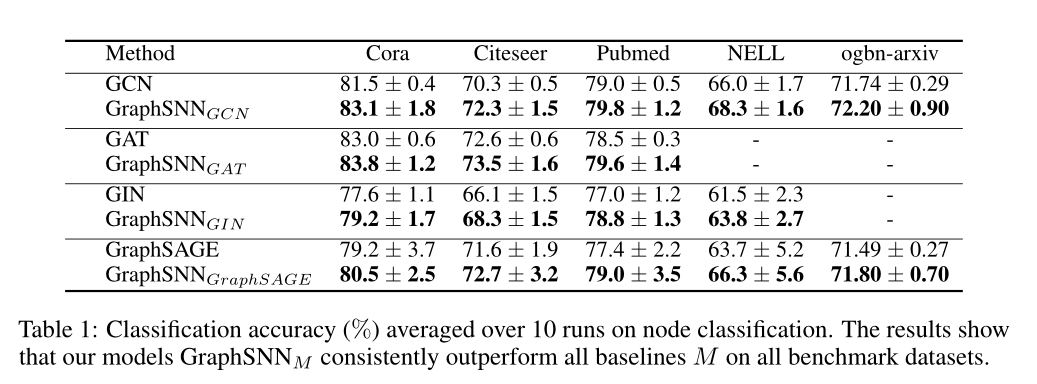
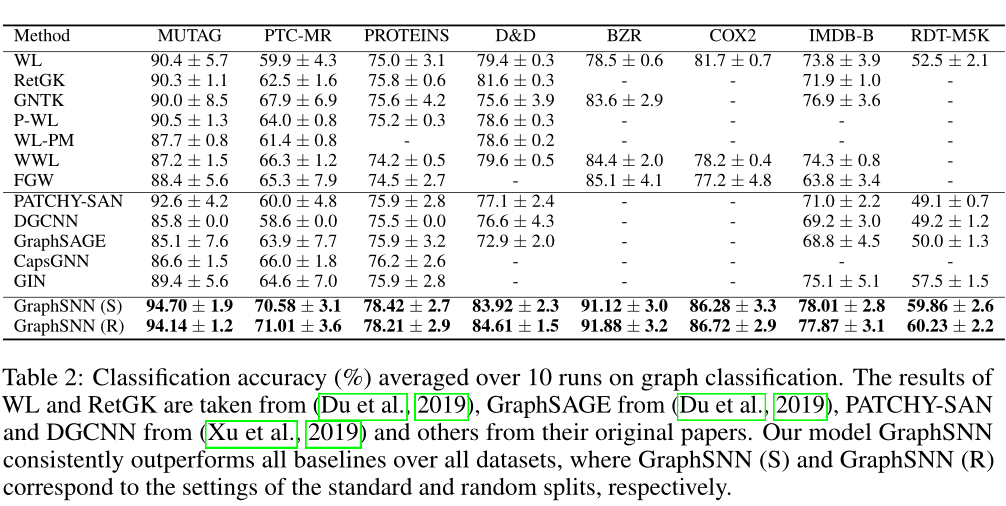
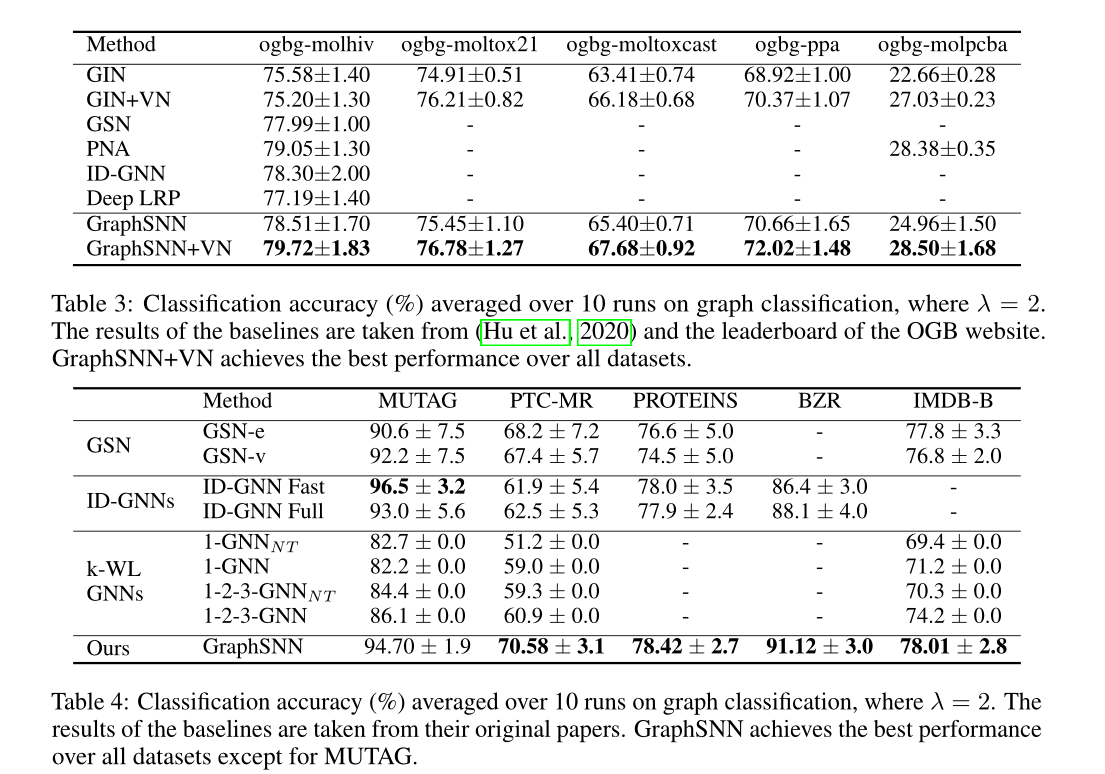
消融实验

• λ=1：捕捉局部密度，两个重叠子图的顶点数量可能会有很大差异，但它们的局部密度可能非常接近，注入这种局部密度有助于提高节点分类的性能
• λ=2：局部相似性，两个重叠子图的相似程度。两个顶点数量相差很大的重叠子图将具有非常不同的结构系数。由于图分类需要比较两个图的相似性，因此λ=2是最好的

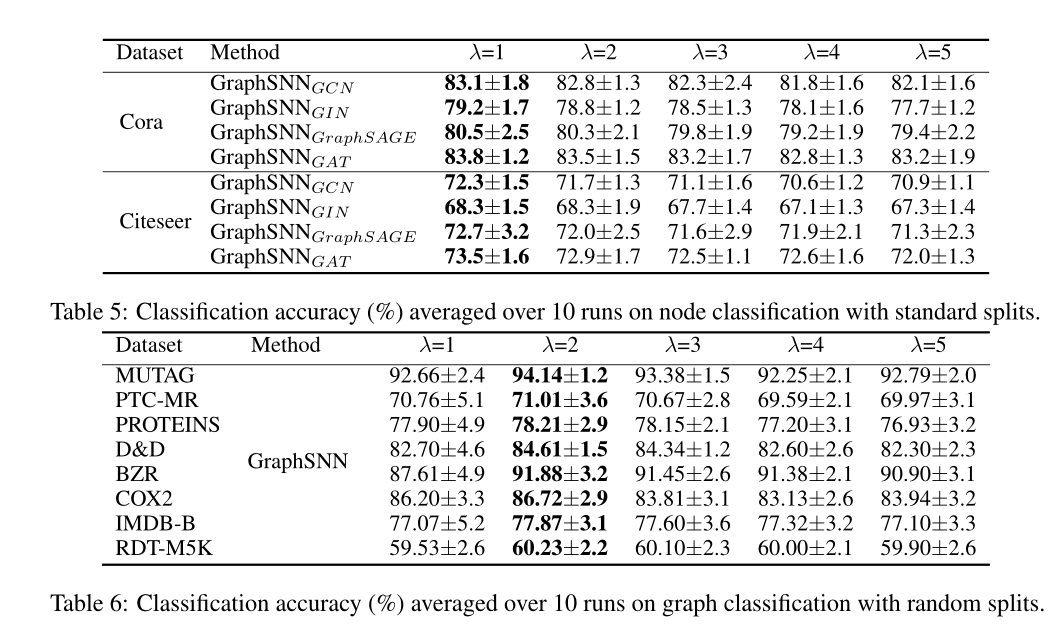
过拟合分析

5 感想

• 这篇文章给人的第一印象就是很amazing。原本我们认为，基于消息聚合的GNN到顶了也就是WL test，但是这篇文章题提出了GIN的一个问题：只考虑了邻居节点，但是没有考虑邻居结构（即边）。将邻居结构考虑进去之后，GNN甚至可以超过WL test了。
• 这也给了我们一个启示：一方面我们需要知道模型的上限，这样不会做无谓的尝试。但是另一方面，模型的上限并不是不变的，需要清晰地知道模型上限对应的前提条件，一旦这个条件被突破了，相应的上限就变了。