matlab极点配置已知超调量,一级倒立摆MATLAB仿真、能控能观性分析、数学模型、极点配置...

题目一：

考虑如图所示的倒立摆系统。图中，倒立摆安装在一个小车上。这里仅考虑倒立摆在图面内运动的二维问题。倒立摆系统的参数包括：摆杆的质量(摆杆的质量在摆杆中心)、摆杆的长度、小车的质量、摆杆惯量等。

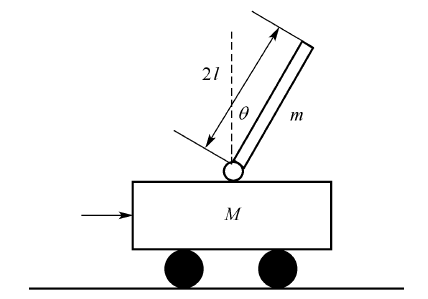
图倒立摆系统

设计一个控制系统，使得当给定任意初始条件(由干扰引起)时，最大超调量 %≤10%，调节时间ts ≤4s ，使摆返回至垂直位置，并使小车返回至参考位置(x=0)。

要求：1、建立倒立摆系统的数学模型

2、分析系统的性能指标——能控性、能观性、稳定性

3、设计状态反馈阵，使闭环极点能够达到期望的极点，这里所说的期望的极点确定

是把系统设计成具有两个主导极点，两个非主导极点，这样就可以用二阶系统的

分析方法进行参数的确定

4、用MATLAB 进行程序设计，得到设计后系统的脉冲响应、阶跃响应，绘出相应状

态变量的时间响应图。

解：

1 建立一级倒立摆系统的数学模型

1.1 系统的物理模型

如图1所示，在惯性参考系下，设小车的质量为M ，摆杆的质量为m ，摆杆长度为l，在某一瞬间时刻摆角(即摆杆与竖直线的夹角)为θ，作用在小车上的水平控制力为u。这样，整个倒立摆系统就受到重力,水平控制力和摩擦力的3外力的共同作用。