非线性系统【八】|线性系统的能观性与能控性 对于如下系统 X ˙ = A X + B U Y = C X \dot{X} = AX + BU\\ Y=CX X˙=AX+BUY=CX 其中 X X X为状态量， Y Y Y为观测量 能控性 格拉姆矩阵判据 系统完全能控的充要条件是存在常数 T > 0 T>0 T>0，使得矩阵 W c ( 0 , T ) = ∫ 0 T e − A t

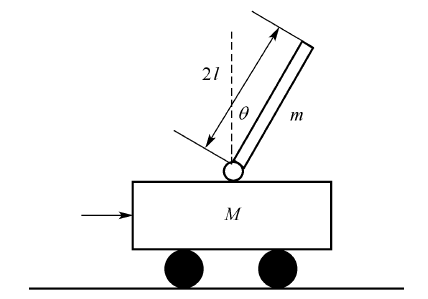
题目一： 考虑如图所示的倒立摆系统。图中，倒立摆安装在一个小车上。这里仅考虑倒立摆在图面内运动的二维问题。倒立摆系统的参数包括：摆杆的质量(摆杆的质量在摆杆中心)、摆杆的长度、小车的质量、摆杆惯量等。 图倒立摆系统 设计一个控制系统，使得当给定任意初始条件(由干扰引起)时，最大超调量 %≤10%，调节时间ts ≤4s ，使摆返回至垂直位置，并使小车返回至参考位置(x=0)。 要求：1、建立倒立