大叔学ML第四：线性回归正则化

目录

• 基本形式
• 梯度下降法中应用正则化项
• 正规方程中应用正则化项
• 小试牛刀
• 调用类库
• 扩展

正则：正则是一个汉语词汇，拼音为zhèng zé，基本意思是正其礼仪法则；正规；常规；正宗等。出自《楚辞·离骚》、《插图本中国文学史》、《东京赋》等文献。 —— 百度百科

基本形式

线性回归模型常常会出现过拟合的情况，由于训练集噪音的干扰，训练出来的模型抖动很大，不够平滑，导致泛化能力差，如下所示：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeaturesdef poly4(X, *theta):return theta[0] + theta[1] * X + theta[2] * X**2 + theta[3] * X**3 + theta[4] * X**4''' 创建样本数据 '''
X = np.arange(0, 9, 1)
Y = [-10, 1, 10, 19, 10, 10, 46, 49, 50]''' 用4次多项式拟合 '''
pf = PolynomialFeatures(degree=4)
featrues_matrix = pf.fit_transform(X.reshape(9, 1))theta = tuple(np.dot(np.dot(np.linalg.pinv(np.dot(featrues_matrix.T, featrues_matrix)), featrues_matrix.T), np.array(Y).T))
Ycalculated = poly4(X, *theta)plt.scatter(X, Y, marker='x', color='k')
plt.plot(X, Ycalculated, color='r')
plt.show()

运行结果：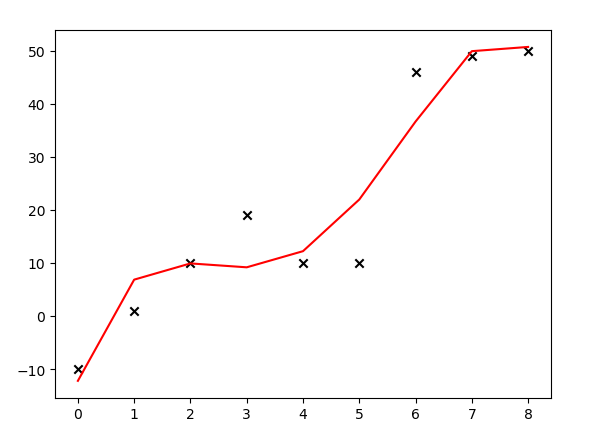

上面的代码中，大叔试图用多项式\(\theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4\)拟合给出的9个样本（如对以上代码有疑问，可参见大叔学ML第三：多项式回归），用正规方程计算出\(\vec\theta\)，并绘图发现：模型产生了过拟合的情况。解决线性回归过拟合的一个方案是给代价函数添加正则化项。代价函数（参见大叔学ML第二：线性回归）形如：
\[j(\theta_0,\theta_1\dots \theta_n)=\frac{1}{2m}\sum_{k=1}^m (\theta_0x_0^{(k)} + \theta_1 x_1^{(k)} + \theta_2 x_2^{(k)} + \dots + \theta_n x_n^{(k)} - y^{(k)})^2 \tag{1}\]
添加正则化后的代价函数形如：
\[j(\theta_0,\theta_1\dots \theta_n)=\frac{1}{2m}\left[\sum_{k=1}^m (\theta_0x_0^{(k)} + \theta_1 x_1^{(k)} + \theta_2 x_2^{(k)} + \dots + \theta_n x_n^{(k)} - y^{(k)})^2 +\lambda\sum_{i=0}^n \theta_i^2 \tag{2}\right]\]，其中\(\lambda > 0\)。直观地理解：当我们不加正则化项时，上面的代码拟合出来的多项式某些项前面的系数\(\theta\)的绝对值可能很大，这将导致横轴数据的微小变化会对应纵轴数据的大幅度变化，使得图像抖动加剧，而加了正则化项后起到一个“惩罚”的作用：当\(\lambda\)较大时，\(\lambda\sum_{i=1}^n \theta_i^2\)会很大，使得代价函数变大，为了使代价函数尽可能地小，\(\theta\)只能取尽可能接近0的数，这样最终模型的抖动就变小了。

梯度下降法中应用正则化项

对（2）式中的\(\vec\theta\)求偏导：

• \(\frac{\partial}{\partial\theta_0}j(\theta_0,\theta_1\dots \theta_n) = \frac{1}{m}\left[\sum_{k=1}^m(\theta_0x_0^{(k)} + \theta_1x_1^{(k)} + \dots+ \theta_nx_n^{(k)} - y^{(k)})x_0^{(k)} + \lambda\theta_0\right]\)
• \(\frac{\partial}{\partial\theta_1}j(\theta_0,\theta_1\dots \theta_n) = \frac{1}{m}\left[\sum_{k=1}^m(\theta_0x_0^{(k)} + \theta_1x_1^{(k)} + \dots+ \theta_nx_n^{(k)}- y^{(k)})x_1^{(k)} + \lambda\theta_1\right]\)
• \(\dots\)
• \(\frac{\partial}{\partial\theta_n}j(\theta_0,\theta_1\dots \theta_n) = \frac{1}{m}\left[\sum_{k=1}^m(\theta_0x_0^{(k)} + \theta_1x_1^{(k)} + \dots+ \theta_nx_n^{(k)}- y^{(k)})x_n^{(k)} + \lambda\theta_n\right]\)

有了偏导公式后修改原来的代码（参见大叔学ML第二：线性回归）即可，不再赘述。

正规方程中应用正则化项

用向量的形式表示代价函数如下：
\[J(\vec\theta)=\frac{1}{2m}||X\vec\theta - \vec{y}||^2 \tag{3}\]
观察（2）式，添加了正则化项的向量表示形式如下：
\[J(\vec\theta)=\frac{1}{2m}\left[||X\vec\theta - \vec{y}||^2 + \lambda||\vec\theta||^2\right] \tag{4}\]
变形：
\[\begin{align} J(\vec\theta)&=\frac{1}{2m}\left[||X\vec\theta - \vec{y}||^2 + ||\vec\theta||^2\right] \\ &=\frac{1}{2m}\left[(X\vec\theta - \vec{y})^T(X\vec\theta - \vec{y}) + \lambda\vec\theta^T\vec\theta \right]\\ &=\frac{1}{2m}\left[(\vec\theta^TX^T - \vec{y}^T)(X\vec\theta - \vec{y}) + \lambda\vec\theta^T\vec\theta\right] \\ &=\frac{1}{2m}\left[(\vec\theta^TX^TX\vec\theta - \vec\theta^TX^T\vec{y}- \vec{y}^TX\vec\theta + \vec{y}^T\vec{y}) + \lambda\vec\theta^T\vec\theta\right]\\ &=\frac{1}{2m}(\vec\theta^TX^TX\vec\theta - 2\vec{y}^TX\vec\theta + \vec{y}^T\vec{y} + \lambda\vec\theta^T\vec\theta)\\ \end{align}\]
对\(\vec\theta\)求导：
\[\begin{align} \frac{d}{d\vec\theta}J(\vec\theta)&=\frac{1}{m}(X^TX\vec\theta-X^T\vec{y} + \lambda I\vec\theta) \\ \frac{d}{d\vec\theta}J(\vec\theta)&=\frac{1}{m}\left[(X^TX + \lambda I)\vec\theta-X^T\vec{y}\right] \end{align}\]
令其等于0，得：\[\vec\theta=(X^TX + \lambda I)^{-1}X^T\vec{y}\tag{5}\]

小试牛刀

对本文开头所给出的代码进行修改，加入正则化项看看效果：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeaturesdef poly4(X, *theta):return theta[0] + theta[1] * X + theta[2] * X**2 + theta[3] * X**3 + theta[4] * X**4''' 创建样本数据 '''
X = np.arange(0, 9, 1)
Y = [-10, 1, 10, 19, 10, 10, 46, 49, 50]''' 用4次多项式拟合 '''
pf = PolynomialFeatures(degree=4)
featrues_matrix = pf.fit_transform(X.reshape(9, 1))ReM = np.eye(5) #正则化矩阵
ReM[0, 0] = 0theta1 = tuple(np.dot(np.dot(np.linalg.pinv(np.dot(featrues_matrix.T, featrues_matrix) + 0 * ReM), featrues_matrix.T), np.array(Y).T))
Y1 = poly4(X, *theta1)theta2 = tuple(np.dot(np.dot(np.linalg.pinv(np.dot(featrues_matrix.T, featrues_matrix) + 1 * ReM), featrues_matrix.T), np.array(Y).T))
Y2 = poly4(X, *theta2)theta3 = tuple(np.dot(np.dot(np.linalg.pinv(np.dot(featrues_matrix.T, featrues_matrix) + 10000 * ReM), featrues_matrix.T), np.array(Y).T))
Y3 = poly4(X, *theta3)plt.scatter(X, Y, marker='x', color='k')
plt.plot(X, Y1, color='r')
plt.plot(X, Y2, color='y')
plt.plot(X, Y3, color='b')plt.show()

运行结果：

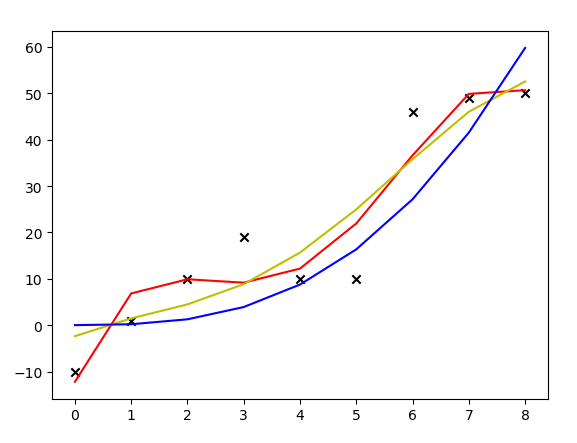
上图中，红线是没有加正则化项拟合出来的多项式曲线，黄线是加了\(\lambda\)取1的正则化项后拟合出来的曲线，蓝线是加了\(\lambda\)取10000的正则化项拟合出来的曲线。可见，加了正则化项后，模型的抖动变小了，曲线变得更加平滑。

调用类库

sklean中已经为我们写好了加正则化项的线性回归方法，修改上面的代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeaturesdef poly4(X, *theta):return theta[0] + theta[1] * X + theta[2] * X**2 + theta[3] * X**3 + theta[4] * X**4''' 创建样本数据 '''
X = np.arange(0, 9, 1)
Y = [-10, 1, 10, 19, 10, 10, 46, 49, 50]''' 用4次多项式拟合 '''
pf = PolynomialFeatures(degree=4)
featrues_matrix = pf.fit_transform(X.reshape(9, 1))ridge_reg = Ridge(alpha=100)
ridge_reg.fit(featrues_matrix, np.array(Y).reshape((9, 1)))
theta = tuple(ridge_reg.intercept_.tolist() + ridge_reg.coef_[0].tolist())Y1 = poly4(X, *theta)plt.scatter(X, Y, marker='x', color='k')
plt.plot(X, Y1, color='r')plt.show()

运行结果：

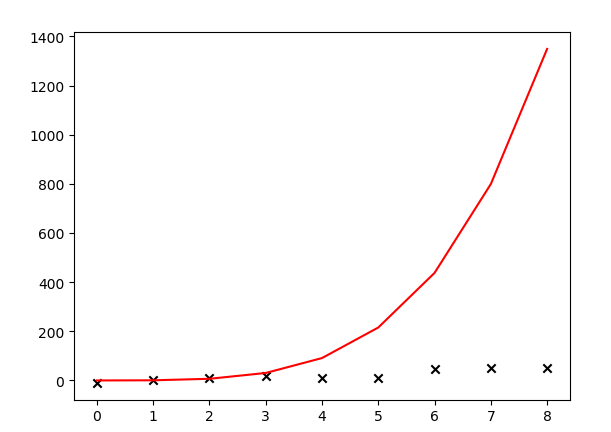
哇，调库和自己写代码搞出的模型差距居然这么大。看来水很深啊，大叔低估了ML的难度，路漫漫其修远兮......将来如果有机会需要阅读一下这些库的源码。大叔猜测是和样本数量可能有关系，大叔的样本太少，自己瞎上的。园子里高人敬请在评论区指教哦。

扩展

正则化项不仅如本文一种添加方式，本文所用的加\(\lambda||\vec\theta||^2\)的方式被称为“岭回归”，据说是因为给矩阵\(X^TX\)加了一个对角矩阵，此对角矩阵的主元看起来就像一道分水岭，所以叫“岭回归”。代码中用的sklean中的模块名字就是Ridge，也是分水岭的意思。

除了岭回归，还有“Lasso回归”，这个回归算法所用的正则化项是\(\lambda||\vec\theta||\)，岭回归的特点是缩小样本属性对应的各项\(\theta\)，而Lasso回归的特点是使某些不打紧的属性对应的\(\theta\)为0，即：忽略掉了某些属性。还有一种回归方式叫做“弹性网络”，是一种对岭回归和Lasso回归的综合应用。大叔在以后的日子研究好了还会专门再写一篇博文记录。

通过这几天的研究，大叔发现其实ML中最重要的部分就是线性回归，连高大上的深度学习也是对线性回归的扩展，如果对线性回归有了透彻的了解，定能在ML的路上事半功倍，一往无前。祝大家圣诞快乐！