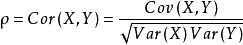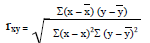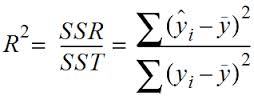回归中的相关度和R平方值（麦子学院）

本文主要是介绍回归中的相关度和R平方值（麦子学院），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

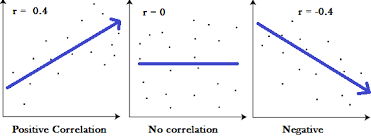
回归中的相关度和R平方值

皮尔逊相关系数 (Pearson Correlation Coefficient):
1.1 衡量两个值线性相关强度的量
1.2 取值范围 [-1, 1]:
正向相关: >0, 负向相关：<0, 无相关性：=0
```
 1.3
```
计算方法举例：

X Y
1 10
3 12
8 24
7 21
9 34

其他例子：
R平方值:

4.1定义：决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例。

4.2 描述：如R平方为0.8，则表示回归关系可以解释因变量80%的变异。换句话说，如果我们能控制自变量不变，则因变量的变异程度会减少80%

4.3：简单线性回归：R^2 = r * r
多元线性回归：

这里写图片描述

R平方也有其局限性：R平方随着自变量的增加会变大，R平方和样本量是有关系的。因此，我们要到R平方进行修正。修正的方法：

import numpy as np
import math
import matplotlib.pylab as plt
from bokeh.charts.builders.scatter_builder import Scatterdef computeCorrelation(X, Y):xBar = np.mean(X)yBar = np.mean(Y)varX=0varY=0SSR = 0for i  in range(len(X)):diffXXBar = X[i] - xBardiffYYbar = Y[i] - yBar SSR += diffXXBar*diffYYbarvarX += diffXXBar**2varY += diffYYbar**2SST= math.sqrt(varX*varY)return SSR/SST
def ployfit(x, y, degree):result={}coffs = np.polyfit(x,y, degree)result['polynomial']=coffs.tolist()
#     print coffsp= np.poly1d(coffs)
#     print pyhat = p(x)
#     print yhat," ----"fig.scatter(x,yhat)ybar=np.sum(y)/len(y)ssreg=np.sum((yhat-ybar)**2)sstot=np.sum((y-ybar)**2)result['determination']=ssreg/sstotreturn result
fig=plt.subplot() 
testX = [1, 3, 8, 7, 9]
testY = [10, 12, 24, 21, 34]
r = computeCorrelation(testX, testY)  
print 'r:',r
print "r*r:",r*r
result=ployfit(testX, testY, 1)
print result
fig.scatter(testX,testY,color="green")
plt.show()

这篇关于回归中的相关度和R平方值（麦子学院）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！