本文主要是介绍3D目标检测实战 | 图解KITTI数据集评价指标AP R40(附Python实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 1 准确率和召回率
- 2 P-R曲线的绘制
- 3 AP R11与AP R40标准
- 4 实际案例
1 准确率和召回率
首先给出 T P TP TP、 F P FP FP、 F N FN FN、 T N TN TN的概念
- 真阳性
True PositiveT P TP TP
预测为正(某类)且真值也为正(某类)的样本数,可视为 I o U > I o U t h r e s h o l d \mathrm{IoU>IoU_{threshold}} IoU>IoUthreshold的检测框数量 - 假阳性
False PositiveF P FP FP
预测为正(某类)但真值为负(另一类)的样本数,可视为 I o U ≤ I o U t h r e s h o l d \mathrm{IoU\le IoU_{threshold}} IoU≤IoUthreshold的检测框数量 - 真阴性
True NegativeT N TN TN
预测为负(不是某类)且真值也为负(不是某类)的样本数 - 假阴性
False NegativeF N FN FN
预测为负(不是某类)但真值为正(某类)的样本数,即在真值区域没有给出检测框
基于上述概念给出准确率和召回率的计算方法
- 准确率
Precision
P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
- 召回率
Recall
R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
准确率 P P P又称为查准率,反映了目标检测的正确性;召回率 R R R又称为查全率,反映了目标检测的泛化性。



2 P-R曲线的绘制
P-R性能也称为准确率-召回率性能,或称查准率-查全率性能,常用于信息检索、Web推荐引擎等应用中。体现P-R性能的主要是P-R曲线,P-R曲线是用于评估二分类模型性能的重要工具,它展示了在不同阈值下模型的准确率和召回率之间的变化关系
P-R曲线的绘制过程是:将预测置信度从高到低排序,依次选择置信度为预测阈值(即大于该阈值的判定为正样本,否则为负样本),计算该阈值下的TP、FN、FP,从而得到准确率和召回率,从高到低移动阈值形成P-R曲线
以一个实例说明绘制过程
假设有10个样本,其中正负样本各5个,按照预测置信度从高到低排序,依次计算准确率和召回率

将形成的(Precision, Recall)坐标对画到坐标系上可得

随着样本增加,折现会趋于曲线
3 AP R11与AP R40标准
P-R曲线围成的面积称为平均准确率(Average Precision, AP),用于衡量模型的综合性能
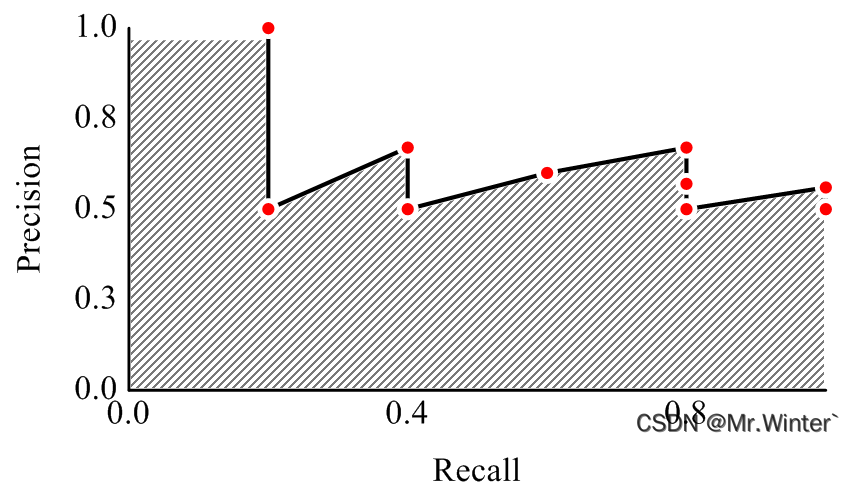
对于面积的计算,一种方法是积分,但由于曲线形态各异,积分比较耗费计算资源;另一种方法是离散化求和,即用若干个矩形面积来近似曲线下面积

具体的公式为
A P ∣ R = 1 ∣ R ∣ ∑ r ∈ R ρ i n t e r ( r ) AP\mid_{R}^{}=\frac{1}{\left| R \right|}\sum_{r\in R}{\rho _{\mathrm{inter}}\left( r \right)} AP∣R=∣R∣1r∈R∑ρinter(r)
其中 R = { r 1 , r 2 , ⋯ , r n } R=\left\{ r_1,r_2,\cdots ,r_n \right\} R={r1,r2,⋯,rn}是等间隔的召回率点, R 11 R_{11} R11和 R 40 R_{40} R40分别指
R 11 = { 0 , 1 10 , 2 10 , ⋯ , 1 } R 40 = { 1 40 , 2 40 , 3 40 , ⋯ , 1 } R_{11}=\left\{ 0,\frac{1}{10},\frac{2}{10},\cdots ,1 \right\} \\ R_{40}=\left\{ \frac{1}{40},\frac{2}{40},\frac{3}{40},\cdots ,1 \right\} R11={0,101,102,⋯,1}R40={401,402,403,⋯,1}
相当于把召回率等分为 ∣ R ∣ \left| R \right| ∣R∣个矩形,高度为P-R曲线在该召回率点的准确度。但问题是可能原曲线在该点没有计算准确度指(因为本质上还是离散曲线),因此就引入准确度插值函数
ρ i n t e r ( r ) = max r ′ : r ′ > r ρ ( r ′ ) \rho _{\mathrm{inter}}\left( r \right) =\max _{r':r'>r}\rho \left( r' \right) ρinter(r)=r′:r′>rmaxρ(r′)
就是取召回率为 r ′ r' r′的位置之后所有准确率的最大值,作为该点的插值准确率,相当于把P-R曲线化成阶梯矩形,如下图蓝色曲线所示,接着按公式计算即可

R 40 R_{40} R40一定程度上削弱了 R 11 R_{11} R11在准确率很低时,AP结果仍然很高的情况,举例而言
假设一个场景中有20个
Ground Truth,但是算法只给出了一个检测结果,且检测的IoU大于阈值,即这是一个TP样本。该置信度下, P r e c i s i o n = 1.0 Precision=1.0 Precision=1.0, R e c a l l = 1 20 = 0.05 Recall=\frac{1}{20}=0.05 Recall=201=0.05
- 计算 A P ∣ R 11 = 1 11 = 0.0909 AP\mid_{R_{11}}^{}=\frac{1}{11}=0.0909 AP∣R11=111=0.0909,这里的1对应 R 11 R_{11} R11中召回点0,而这个准确率已经超过了很多单目3D检测算法的准确率,显然不合理
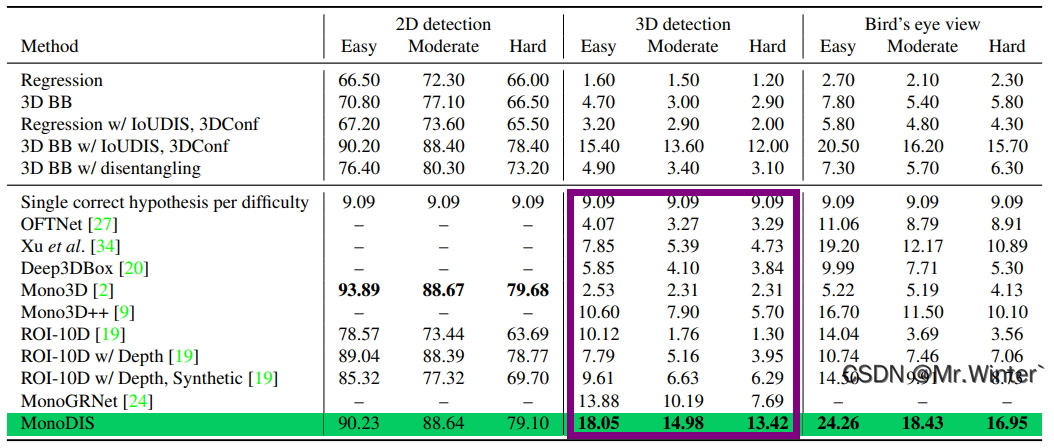
- 计算 A P ∣ R 40 = 1 + 1 40 = 0.05 AP\mid_{R_{40}}^{}=\frac{1+1}{40}=0.05 AP∣R40=401+1=0.05,这里的1对应 R 40 R_{40} R40中召回点 1 40 \frac{1}{40} 401和 2 40 \frac{2}{40} 402
目前KITTI官方也认可了 A P ∣ R 40 AP\mid_{R_{40}}^{} AP∣R40指标,后续基本也采用 A P ∣ R 40 AP\mid_{R_{40}}^{} AP∣R40进行实验评估
以下是KITTI数据集AP检测的实例
Car AP@0.70, 0.70, 0.70:
bbox AP:90.7769, 89.7942, 88.8813
bev AP:90.0097, 87.9282, 86.4528
3d AP:88.6137, 78.6245, 77.2243
aos AP:90.75, 89.66, 88.66
Car AP_R40@0.70, 0.70, 0.70:
bbox AP:95.5825, 94.0067, 91.5784
bev AP:92.4184, 88.5586, 87.6479
3d AP:90.5534, 81.6116, 78.6108
aos AP:95.55, 93.85, 91.33
解释如下:
-
第一行
Car AP@0.70, 0.70, 0.70Car表示类别,AP表示基于AP R11的平均准确率,后面三个0.70分别指代2D检测框、BEV检测框和3D检测框的IoU阈值,即大于这个阈值才认为是正样本 -
第二、三、四行
每一行指代一种检测模式,即2D检测框、BEV检测框和3D检测框,每一行的三个数值分别对应Easy、Moderate和Hard三种检测难度的的结果,难度越大(例如遮挡严重),检测准确度越小 -
第五行
aos表示平均朝向相似度(average orientation similarity),用于评价预测输出的朝向与真实框朝向的相似程度
4 实际案例
在KITTI数据集中,按以下步骤计算AP数值
-
计算IoU,这部分原理参考3D目标检测实战 | 详解2D/3D检测框交并比IoU计算(附Python实现)
frame_overlaps, parted_overlaps, gt_num, dt_num = iou(gt_annos, dt_annos, method, num_parts) -
以0置信度阈值计算置信度列表,即只要IoU符合条件的都视为TP样本,提取其置信度评分
rets = compute(frame_overlaps[i], gt_data_list[i], dt_data_list[i],ignored_gts[i], ignored_dts[i], min_overlap=min_overlap, thresh=0.0) _, _, _, _, scores_i = rets -
对置信度列表均匀采样41个点,得到40个召回点对应的置信度阈值
thresholds = getThresholds(np.array(scores), valid_gt_num)def getThresholds(scores: np.ndarray, num_gt, num_sample_pts=41):scores.sort()scores = scores[::-1]current_recall = 0thresholds = []for i, score in enumerate(scores):l_recall = (i + 1) / num_gtif i < (len(scores) - 1):r_recall = (i + 2) / num_gtelse:r_recall = l_recallif (((r_recall - current_recall) < (current_recall - l_recall))and (i < (len(scores) - 1))):continuethresholds.append(score)current_recall += 1 / (num_sample_pts - 1.0)return thresholds -
遍历每个阈值,计算该阈值下的TP、FP和FN,从而计算准确率和召回率
for i in range(len(thresholds)):recall[m, l, k, i] = pr[i, 0] / (pr[i, 0] + pr[i, 2])precision[m, l, k, i] = pr[i, 0] / (pr[i, 0] + pr[i, 1])if compute_aos:aos[m, l, k, i] = pr[i, 3] / (pr[i, 0] + pr[i, 1]) -
取PR曲线外接矩形
for i in range(len(thresholds)):precision[m, l, k, i] = np.max(precision[m, l, k, i:], axis=-1)recall[m, l, k, i] = np.max(recall[m, l, k, i:], axis=-1)if compute_aos:aos[m, l, k, i] = np.max(aos[m, l, k, i:], axis=-1) -
计算AP
def mAP(prec):sums = 0for i in range(0, prec.shape[-1], 4):sums = sums + prec[..., i]return sums / 11 * 100def mAPR40(prec):sums = 0for i in range(1, prec.shape[-1]):sums = sums + prec[..., i]return sums / 40 * 100
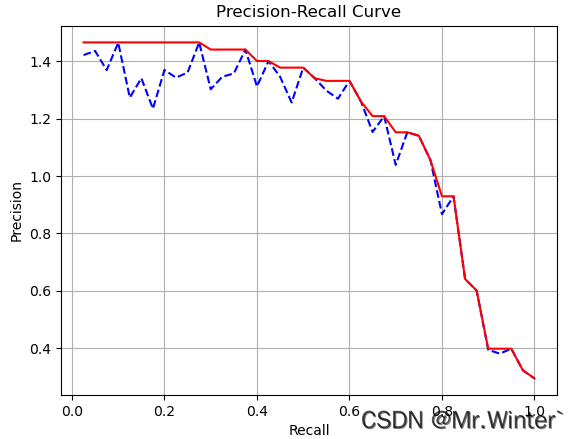
本文完整工程代码请通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
这篇关于3D目标检测实战 | 图解KITTI数据集评价指标AP R40(附Python实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




