本文主要是介绍高数 | 定理及性质证明 | 含有第一类间断点和无穷间断点的函数f(z)在包含该间断点的区间内必没有原函数F(z).,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
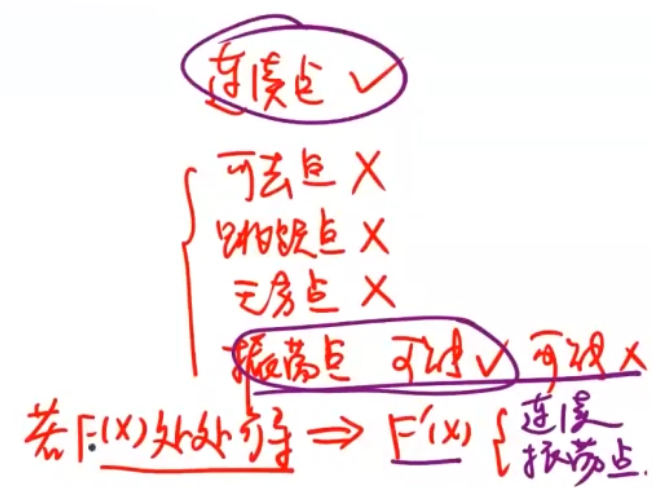
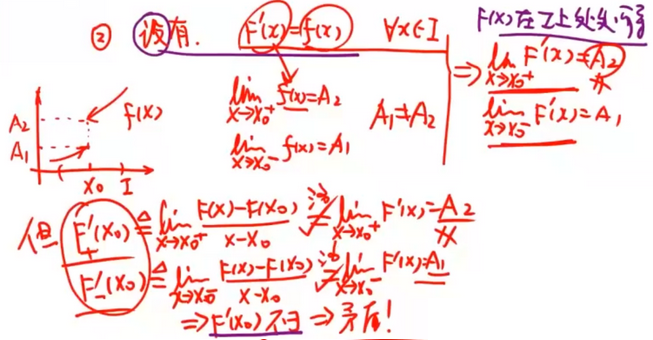
含有第一类间断点和无穷间断点的函数f(z)在包含该间断点的区间内必没有原函数F(z).
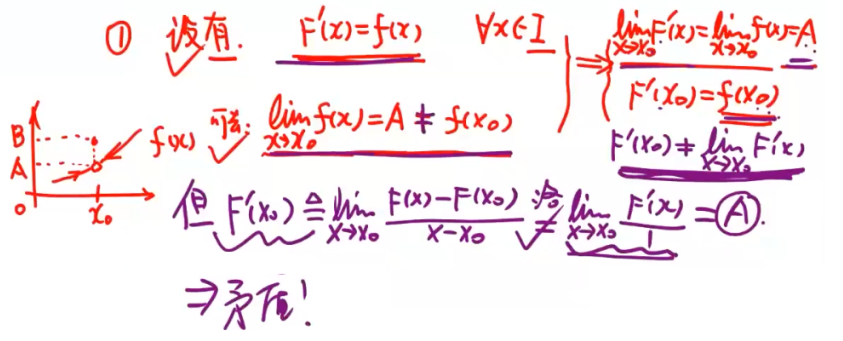



可导函数的导函数一定连续吗? - 知乎
综合以上几点﹐可以得出重要结论:
可导函数F(x)求导后的函数F'(x)=f(z)不一定是连续函数,
但是如果有间断点,一定是第二类间断点(在考研的范畴内,只能是振荡间断点).
也可以从导数介值定理的方面来证明
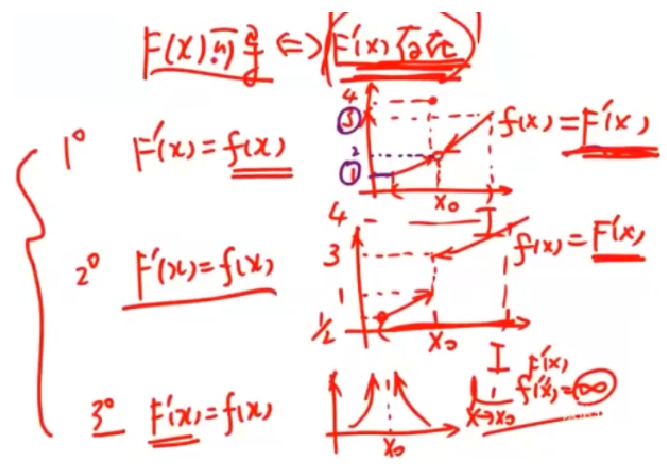
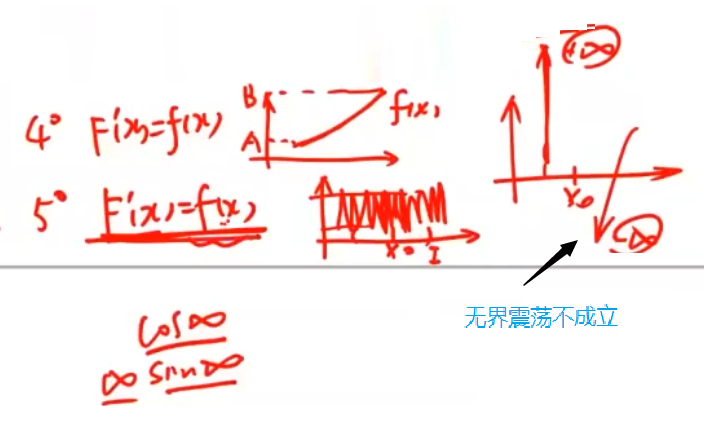
例题

震荡虽然有原函数,但不一定是那个积分!
这篇关于高数 | 定理及性质证明 | 含有第一类间断点和无穷间断点的函数f(z)在包含该间断点的区间内必没有原函数F(z).的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!