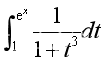要找函数 f ( x ) f(x) f(x) 的一个原函数（即不定积分），可以按照以下步骤进行： 确定形式：首先判断 f ( x ) f(x) f(x) 是什么类型的函数，例如多项式、指数函数、对数函数、三角函数等。 使用积分公式：根据不同的函数类型，使用相应的积分公式。 对于多项式函数 f ( x ) = x n f(x) = x^n f(x)=xn，其原函数是 ∫ x n \int

利用勒让德多项式进行拟合的区域是[-1,1]，如果不是这个区域，比如是[a,b]，利用转化到[-1,1]。 参考以下例题计算系数 C语言代码如下 //用三阶的勒让德多项式进行拟合#include<math.h>#include<stdio.h>#include "main.c"double f(double x);double fl1(double x);double f

微信公众号：python宝关注可了解更多的python相关知识。若有问题或建议，请公众号留言; 内容目录 一、激活函数简介二、Sigmoid三、tanh四、ReLU      五、其它激活函数及饱和度 一、激活函数简介     深度学习的发展一般分为三个阶段，感知机-->三层神经网络-->深度学习（表示学习）。早先的感知机由于采用线性模型，无法解决异或问题，表示能力受到限制。为此三层神经网络

目录 1、f(x)存在 2、f'(x)存在 3、原函数（不定积分）存在定理 4、定积分存在定理 1、f(x)存在 （1）f(x)在一点极限存在  ≠> f(x)在这一点连续 （2）f(x)存在 ≠> f(x)有介质性 （3）f(x)可导  +    =>  f'(x)在x0连续 证明： 2、f'(x)存在 （1）f'(x)存在 => f'(x)有介质性（达

如图碰到该题该怎么解？ 在纸上按①②③的顺序写出这个，其中①是最主要的 第②步和第③步就是在用反函数时要用到的逻辑思维，不是一起用的，你需要用②才去用②，你需要用③才去用③ 在纸上先写出第①步，即 其中， 第②步， 由步骤①的在它的上方写它的原函数，等于左边的反变量x（也就是反函数的变量x） 第③步， 由步骤①的在它的下方写它的原函数，等于右边的

含有第一类间断点和无穷间断点的函数f(z)在包含该间断点的区间内必没有原函数F(z).   可导函数的导函数一定连续吗？ - 知乎 综合以上几点﹐可以得出重要结论: 可导函数F(x)求导后的函数F'(x)=f(z)不一定是连续函数, 但是如果有间断点，一定是第二类间断点(在考研的范畴内,只能是振荡间断点).  也可以从导数介值