本文主要是介绍内部矩阵维度必须一致simulink_基于主成分分析 沪深300个股一致性IF股指交易策略...,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

策略概述
一般而言,趋势策略在市场有趋势的时候盈利丰厚,而在震荡市场,趋势策略容易发生亏损。
我们可以通过对市场的趋势和震荡进行判断,使策略具有更好的收益表现。此前,我们发布了一系列报告,用来衡量市场趋势的强度,在此基础上进行交易,而在震荡市场,则放弃进行趋势交易。
本篇专题报告从市场成份股的一致性强弱出发,对市场指数的趋势强弱进行判断。本篇报告所选择的主要标的是沪深 300 指数,对应的是沪深 300 成份股。从直观上来看,成份股一致性用来表示市场的成份股走势是否同涨同跌。
图1展示了成份股一致性较强的时候,3个(标准化之后)股价序列的走势;图2展示了成份股一致性较弱的时候,股价序列的走势。从直观上来看,图1中成份股序列走势相似性高,而图2中成份股序列走势之间的相似性弱。在成份股一致性较强的市场,成份股同涨同跌,容易形成市场“合力”,产生较大的波动和趋势。而在成份股一致性较弱的市场,成份股随机波动,市场不易产生趋势。因而我们可以基于对市场成份股一致性强弱的计算,对市场的趋势进行估计,从而确定是否进行趋势交易。
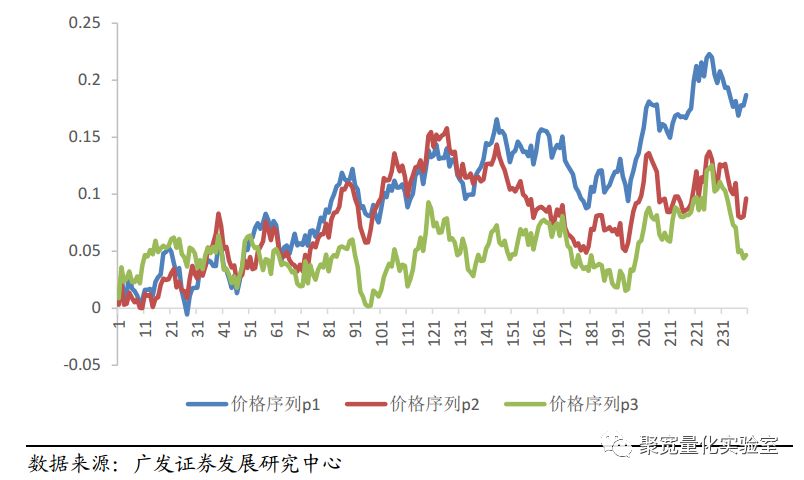
图1:成分股一致性强
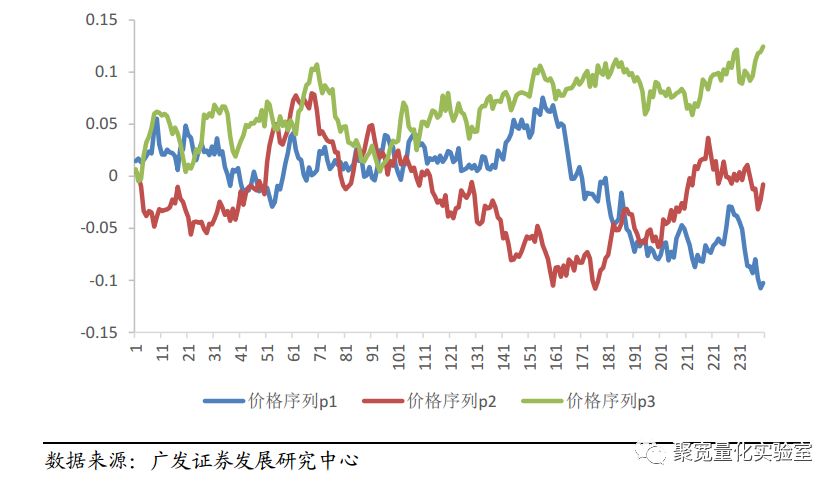
图2:成分股一致性弱
策略构造
1.算法原理
主成分分析:
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1、2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
这些方差也被称为特征值,方差越大代表映射后信噪比越好,通过忽略n-k个特征值无限接近于0的向量构造k维新映射。而每一个特征值就能反应映射携带信息强度。
2.模型构造
我们首先获取一个规模为(n,m)的矩阵,m是样本股票数量,n为回望周期等频率价格采样次数,也就是如果以一年作为回望周期,采样频率为每日,样本为个股当日收盘价,选取股票池为沪深300指数中全部成分股,那么n=365,m=300(假定365天每天都是交易日,当然现实情况不是这样的)。这个矩阵每一个元素都是一个价格数据,矩阵列向量就代表某只股票当年全部每日收盘价的时间序列。然后我们对矩阵中数据进行标准化处理,常用做法在每个列向量中,把此列所有的元素值除以此列第一个值。处理后图示如下:
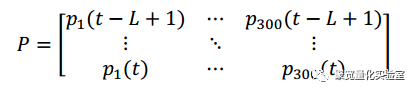
计算价格矩阵P的协方差矩阵E
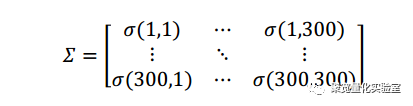
同时我们可以观察到,我们可以对P矩阵进行线性变化,使得这个(n*m)维矩阵变为一个n维向量,我们一共可以找到无穷个这样的线性向量对P进行变换,我们取300个,因为这样可以使得这些线性变换向量拼接在一起也组成一个和P规模相等的矩阵,方便我们接下来进行分析。设变换矩阵为U
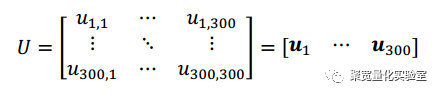
而Q=PU=[Pu1...Pu200],其中为一个n维价格时间序列。
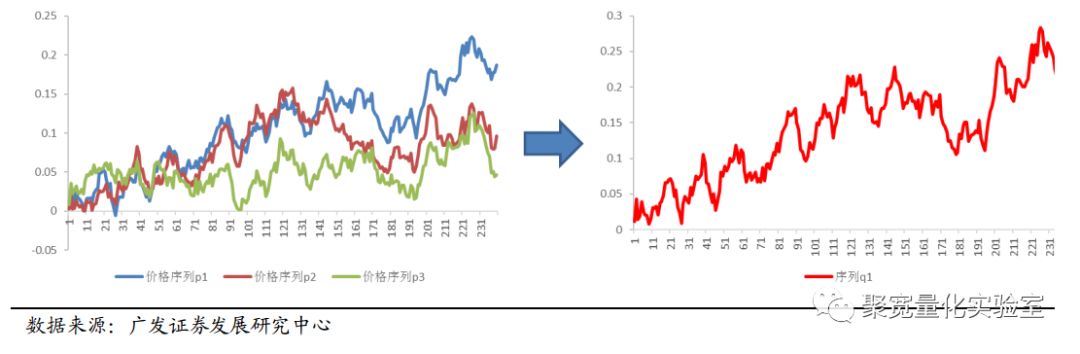
图3:价格序列线性变换(例)
而如果我们对U进行一些线性约束的话,U就会具有一些有趣的性质。在这里,我们让
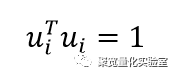
我们可以发现,矩阵U就可以用协方差矩阵E替代。即问题变成了求解:

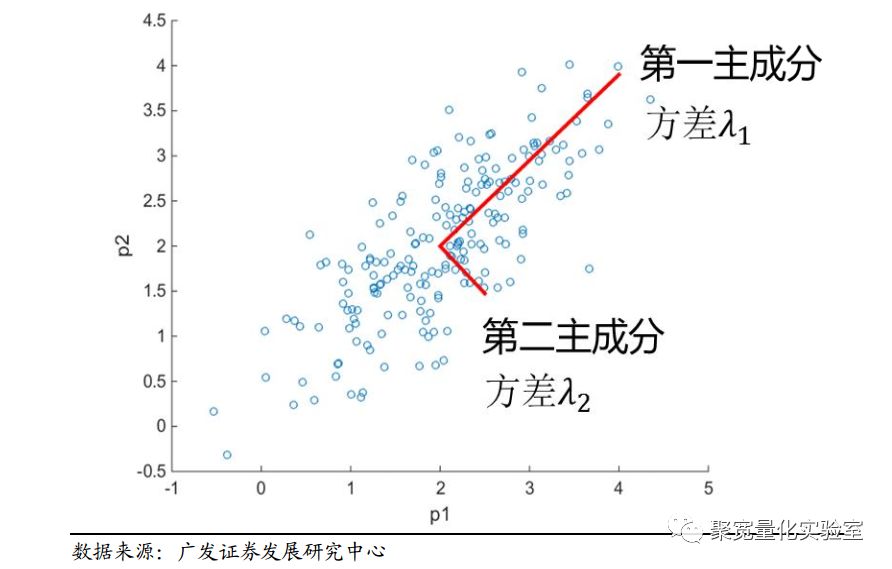
因而定义一致性指标如下:
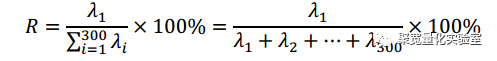
λ1为协方差矩阵奇异值分解中最大的λ,即第一主成分。
一致性指标R是0到1之间的数,R越大,说明成份股之间一致性越强;R越小,说明成份股之间的一致性越弱。
以沪深300为例,下图是2006年1月1日至2016年7月15日沪深300指数的一致性指标分析结果。在每天收盘时,采用最近连续20个交易日的30分钟收盘价计算一致性指标R。其中红色的点位是沪深300成分股一致性指标75%分位数及以上出现的时间。
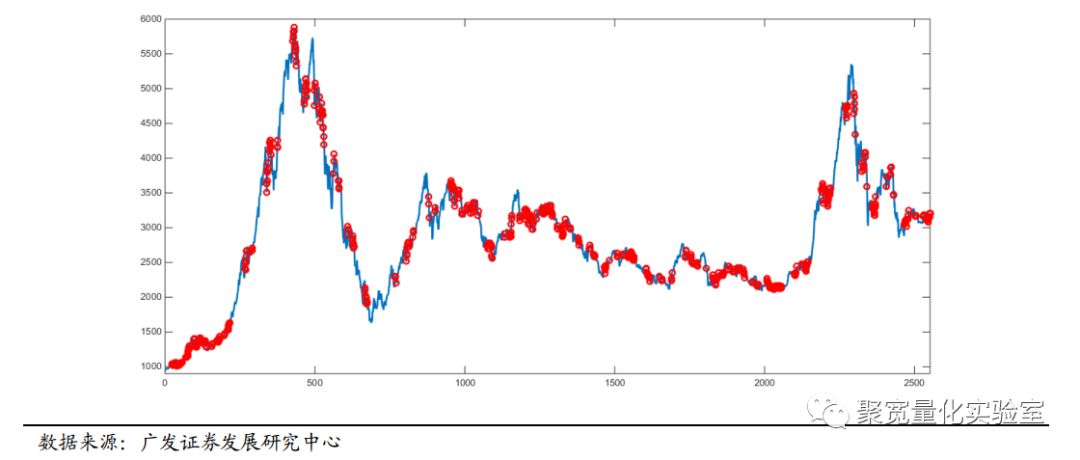
由图可见,市场成份股一致性指标的强弱与市场的趋势和震荡划分具有很明显的关联。
3.策略设计
当沪深 300 指数成份的一致性比较强的时候,进行趋势跟踪交易;当成份股的一致性弱的时候,认为当天不适合趋势交易。交易的开仓方向和n日内趋势动量方向一致。通过预设阈值,一旦当日一致性R值突破阈值,则认为目前趋势动量较强,则:
开多 P(t) - P(t-n) > 0
开空 P(t) - P(t-n) > 0
P(t)为第t天的沪深300股指价格,P(t-n)为n日前沪深300指数价格,n为模型计算R的采样回望天数。
止损方式为追踪止损,当持仓亏损点数超过两倍ATR(真实波幅)则出场止损。
同时为了防止一致性指标R直接设置阈值的主观性给模型带来幸存者偏差,对R值序列进行移动平均,阈值R_standard为:
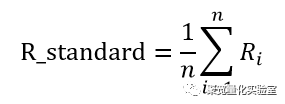
实证检验
为了检验策略的有效性,在聚宽平台设计了以python为语言的策略代码。时间窗口选取2015年1月1日到2018年12月27日,绩效表现如下:
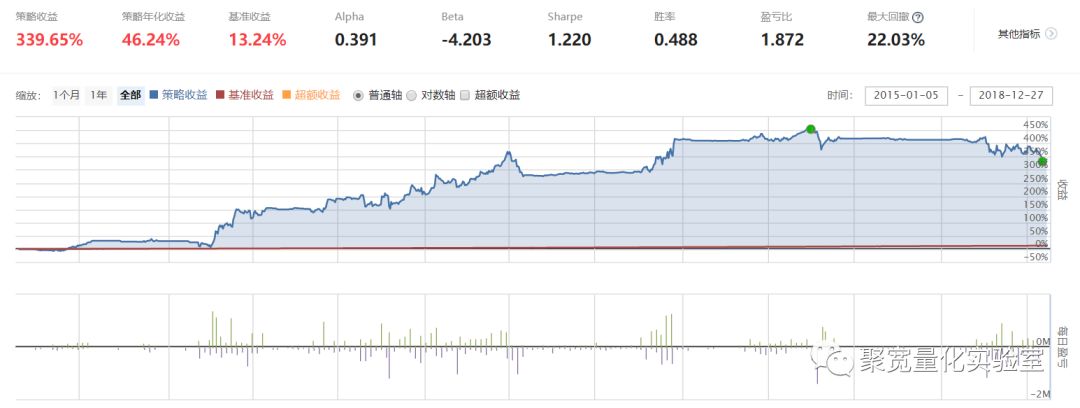
为了保持鲁棒性,我们没有做过多的参数优化,持仓周期,R值计算的回望周期,都使用同样的时间窗口进行回溯,调整持仓时间设置为固定每周一,来避免主管设置周期产生的路径依赖。
我们看到,策略取得了较好的绩效,并且风险和回撤都把握在一定的范围内,具有一定程度稳定的超额收益能力。报告中策略观点有效。策略源码可以点击下方阅读原文获取。本文参考广发证券研究报告《从成分股一致性衡量市场趋势》思路。

欢迎关注『聚宽量化实验室』
这篇关于内部矩阵维度必须一致simulink_基于主成分分析 沪深300个股一致性IF股指交易策略...的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





