成分专题
【高中生讲机器学习】17. 讲人话的主成分分析，它来了！（上篇）
创建时间：2024-08-13 首发时间：2024-09-05 最后编辑时间：2024-09-05 作者：Geeker_LStar 你好呀~这里是 Geeker_LStar 的人工智能学习专栏，很高兴遇见你~ 我是 Geeker_LStar，一名准高一学生，热爱计算机和数学，我们一起加油~！ ⭐(●’◡’●) ⭐ 那就让我们开始吧！ 诶嘿！这一篇想写很久啦，现在终于来了！（什么玩意都拖到
Python从0到100（五十七）：机器学习-主成分分析机
主成分分析是⼀种常⽤的降维技术，⽤于将⾼维数据集投影到低维空间中，同时保留数据集的主要特征。PCA通过寻找数据中最重要的⽅向（主成分），并将数据投影到这些⽅向上来实现降维。 1.基本原理 1、数据中心化：⾸先，对原始数据进⾏中⼼化处理，即将每个特征的均值减去每个数据点的对应特征值，以确保数据的均值为零。 2、协方差矩阵：然后，计算数据的协⽅差矩阵，该矩阵表示了不同特征之间的关联性。 3、特征值
数据降维技术——PCA（主成分分析）
为什么要对数据进行降维？ 在机器学习或者数据挖掘中，我们往往会get到大量的数据源，这些数据源往往有很多维度来表示它的属性，但是我们在实际处理中只需要其中的几个主要的属性，而其他的属性或被当成噪声处理掉。比如，13*11的源数据经过将为后变成了13*4的优化数据，那么，中间就减去了7个不必要的属性，选取了4个主要属性成分，简化了计算。 常用的数据降维方法有：主成分分析
【产品那些事】什么是软件成分分析(SCA)？
文章目录 前言背景SCA概述 功能组成工作原理软件供应链漏洞检测通用架构组件的数量和检测算法方面基于包管理器(构建)检测技术有那些检测算法？引用开源软件的方式方面漏洞库的积累与颗粒度 SCA产品Depency-Check基本介绍工作原理文件类型分析器工具使用体验Maven插件集成：Dependency-check-mavenCLI方式-安全人员检测CI集成-Jenkins插件：Depend
运用PCA（主成分分析法）进行人脸识别的MATLAB 代码实现
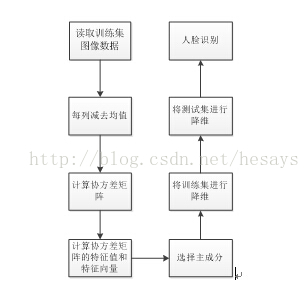
PCA（主成分分析算法）出现的比较早。 PCA算法依赖于一个基本假设：一类图像具有某些相似的特征（如人脸），在整个图像空间中呈现出聚类性，因而形成一个子空间，即所谓特征子空间，PCA变换是最佳正交变换，利用变换基的线性组合可以描述、表达和逼近这一类图像，因此可以进行图像识别，PCA包含训练和识别两个阶段。 训练阶段： 1）计算平均脸 2）计算差值脸 3）构建协方差矩阵 4）计算矩阵的特
2-79 基于matlab的卷积稀疏的形态成分分析的医学图像融合
基于matlab的卷积稀疏的形态成分分析的医学图像融合，基于卷积稀疏性的形态分量分析 (CS-MCA) 的稀疏表示 (SR) 模型，用于像素级医学图像融合。通过 CS-MCA 模型使用预先学习的字典获得其卡通和纹理组件的 CSR。然后，合并所有源图像的稀疏系数，并使用相应的字典重建融合分量。最后，实现融合图像计算。程序已调通，可直接运行。 2-79 卷积稀疏的形态成分分析 - 小红书 (xi
淘宝商品详情API返回值中的商品材质与成分
淘宝商品详情API返回值中关于商品材质与成分的信息，通常作为商品属性的一部分进行返回。这些信息对于消费者了解商品的质量、适用场景以及做出购买决策至关重要。以下是对淘宝商品详情API返回值中商品材质与成分的详细解析： 一、商品材质与成分的表示方式 直接列出：在API返回的JSON或XML格式数据中，商品材质与成分可能会直接以文本形式列出，如“材质：棉100%”、“成分：水、甘油、丙二醇”等。
【机器学习】独立成分分析的基本概念、应用领域、具体实例（含python代码）以及ICA和PCA的联系和区别
引言 独立成分分析（Independent Component Analysis，简称ICA）是一种统计方法，用于从多个观察到的混合信号中提取出原始的独立信号源 文章目录 引言一、独立成分分析1.1 定义1.2 独立成分分析的基本原理1.3 独立成分分析的步骤1.3.1 观察数据收集1.3.2 数据预处理1.3.3 ICA模型建立1.3.4 ICA算法实现1.3.5 源信号提取1.
1系-8系铝合金材料的成分特性及应用详解
1系-8系铝合金材料的成分特性及应用详解 铝合金概述 铝合金的定义铝合金是一种以铝为基体，通过添加一定量的其他合金化元素（如铜、锰、硅、镁、锌等）形成的合金材料。由于合金元素的加入，铝合金在保持铝的轻质、良好导电导热性等基本特性的同时，还具备了更高的强度、更好的铸造和加工性能以及优异的耐腐蚀性。 铝合金的分类铝合金按照成分和加工方式主要分为两大类：变形铝合金和铸造铝合金。变形铝合金：这类合金通过塑
【机器学习】特征工程的基本概念以及LASSO回归和主成分分析优化方法
引言 特征工程是机器学习中的一个关键步骤，它涉及到从原始数据中提取和构造新的特征，以提高模型的性能和预测能力LASSO（Least Absolute Shrinkage and Selection Operator）回归是一种用于回归分析的线性模型，它通过引入L1正则化（Lasso正则化）来简化模型并减少过拟合的风险主成分分析（Principal Component Analysis，PCA）
通过主成分分析实现检测金融中的异常交易模式
主成分分析（PCA）是一种在机器学习和数据科学中广泛使用的降维技术。它的主要目的是将高维数据转换为低维数据，同时尽可能保留原始数据中的信息。以下是PCA的一些关键点： 1. 基本概念：PCA的核心思想是将n维特征映射到k维上，这k维是在原有n维特征的基础上重新构造出来的，它们被称为主成分。这些主成分是相互正交的，即彼此之间没有相关性。 2. 工作原理： - 标准化数据：首先对数据进行标准化处
![[数学建模][2018年A 模拟练习][层次分析法、主成分分析法] 5. 深圳市人才吸引力评价](https://i-blog.csdnimg.cn/direct/e35188a791284544b6e6c40541258b7b.png)
[数学建模][2018年A 模拟练习][层次分析法、主成分分析法] 5. 深圳市人才吸引力评价
文章目录 一、前言二、论文 一、前言 这是我第一次参加校赛、参加数学建模时的一篇论文。当时只是将所学内容进行了一个简单练习。关注点在于：层次分析法、主成分分析法及论文的写作排版。 论文、数据、程序 也都在。如果需要的话，购买专栏后私信我即可。 PS：本篇论文适合当一个简单的课后作业提交，不适合各类比赛提交。截图啥的，没有截太多，需要论文的话，私信我即可。title 有敏感信息
主成分分析与奇异值分解
机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 版权声明： 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用，但请注明出处，如果有问题，请联系wheeleast@gmail.com。也可以加我的微博: @leftnoteasy 转载https://www.cnblogs.com/Left
数学建模学习（115）：主成分分析（PCA）与Python实践
文章目录 一.主成分分析简介1.1 数学背景与维度诅咒1.2 PCA的定义与应用 二.协方差矩阵——特征值和特征向量三.如何为数据集选择主成分数量四.特征提取方法五.LDA——与PCA的区别六.PCA的应用七.PCA在异常检测中的应用八.总结 一.主成分分析简介 1.1 数学背景与维度诅咒 主成成分分析（PCA）是一种广泛使用的算法，用于从高维数据中提取主要特征，以便更有效地
深入理解主成分分析 (PCA) 及其广泛应用
深入理解主成分分析 (PCA) 及其广泛应用 文章目录 深入理解主成分分析 (PCA) 及其广泛应用引言PCA 的核心概念与目标PCA 的几何解释与步骤具体数值计算例子如果 PCA 中维度和执行 PCA 之前的维度保持一致，会发生什么？Python 实现 PCA实例解析：二维数据的 PCA 应用实际应用场景与总结 引言 主成分分析（Principal Compon
主成分分析PCA详解（二）
我不生产自己不熟悉的内容，我只是陌生内容的搬运工！向原作致敬！ 转载自：http://blog.csdn.net/jzwong/article/details/45699097 作者：jzwong 一、简介 PCA（Principal Components Analysis）即主成分分析，是图像处理中经常用到的降维方法，大家知道，我们在处理有关数字图像处理方面的问题时，比如经
主成分分析PCA详解(一)
对理解PCA非常好的一篇文章，留着以防以后忘记 原文来自:博客园（华夏35度）http://www.cnblogs.com/zhangchaoyang 作者:Orisun 降维的必要性 1.多重共线性--预测变量之间相互关联。多重共线性会导致解空间的不稳定，从而可能导致结果的不连贯。 2.高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间，而在十维空间上只有0.02%。
【Python机器学习实战】 | 基于PCA主成分分析技术读入空气质量监测数据进行数据预处理并计算空气质量综合评测结果
🎩 欢迎来到技术探索的奇幻世界👨💻 📜 个人主页：@一伦明悦-CSDN博客 ✍🏻 作者简介： C++软件开发、Python机器学习爱好者 🗣️ 互动与支持：💬评论 👍🏻点赞 📂收藏 👀关注+ 如果文章有所帮助，欢迎留下您宝贵的评论， 点赞加收藏支持我，点击关注，一起进步！ 引言 主成分分析（Principal Component
文本挖掘之降维之特征抽取之主成分分析（PCA）
PCA（主成分分析） 作用： 1、减少变量的的个数 2、降低变量之间的相关性，从而降低多重共线性。 3、新合成的变量更好的解释多个变量组合之后的意义 PCA的原理： 样本X和样本Y的协方差(Covariance)： 协方差为正时说明X和Y是正相关关系，协方差为负时X和Y是负相关关系，协方差为0时X和Y相互独立。 Cov(X,X)就是X的方差(Variance).
mke2fs -- 比mkfs.ext4艺术成分更高
mke2fs 介绍 mke2fs 是一个用于创建 ext2/ext3/ext4 文件系统的工具，是 mkfs.ext2, mkfs.ext3, mkfs.ext4 的底层工具。它提供了丰富的选项和参数，可以对文件系统进行详细的配置和优化。下面是 mke2fs 的详细讲解，包括其主要功能、常用选项及使用示例。 mke2fs 基本用法 mke2fs [options] device [blo
【转】主成分分析（PCA）原理解析
本文转载于 http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html 主成分分析（Principal components analysis）-最大方差解释 在这一篇之前的内容是《Factor Analysis》，由于非常理论，打算学完整个课程后再写。在写这篇之前，我阅读了PCA、SVD和LD
机器学习(V)--无监督学习(二)主成分分析
当数据的维度很高时，很多机器学习问题变得相当困难，这种现象被称为维度灾难（curse of dimensionality）。 在很多实际的问题中，虽然训练数据是高维的，但是与学习任务相关也许仅仅是其中的一个低维子空间，也称为一个低维嵌入，例如：数据属性中存在噪声属性、相似属性或冗余属性等，对高维数据进行降维（dimension reduction）能在一定程度上达到提炼低维优质属性或降噪的效果。
建设高关连度模式 环节词钻研的基础成分
一旦你掌握了要害词分析的手腕，那末你就能够凯旋了，你驾驭了建树高度干系的内容的伎俩、并以此愈合你的来访者和前进可信度。 枢纽词研讨十分的酷，由于这份工作是针对付人们思维的剖析。通过察看人们找工具时候的关键词大要短语是无价的，因为与其听人们讲他们想怎么样做，不如观测他们到底做了甚么。当这些信息统计到一路的时辰，你未必会发明当人们想找某个题目的时刻时时输入甚么。一旦你把握了
微生信神助力：在线绘制发表级主成分分析（PCA）图
主成分分析（Principal components analysis，PCA）是一种线性降维方法。它利用正交变换对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。PCA是一种对数据进行简化分析的技术，这种方法可以有效地找出数据中最“主要”的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭示隐藏