本文主要是介绍傅里叶谱方法-傅里叶谱方法求解二维浅水方程组和二维粘性 Burgers 方程及其Matlab程序实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
3.3.2 二维浅水方程组
二维浅水方程组是描述水波运动的基本方程之一。它主要用于描述近岸浅水区域内的波浪、潮汐等水动力学现象。这个方程组由两个偏微分方程组成,一个是质量守恒方程,另一个是动量守恒方程。浅水方程描述了具有自由表面、密度均匀、深度较浅的液体在重力作用下的流动过程, 用于研究潮波和河流,具体形式如下:
{ ∂ η ∂ t = − ∂ ( η u ) ∂ x − ∂ ( η v ) ∂ y ∂ u ∂ t = − v ∂ u ∂ y − u ∂ u ∂ x − g ∂ η ∂ x ∂ v ∂ t = − u ∂ v ∂ x − v ∂ v ∂ y − g ∂ η ∂ y (3-34) \left\{\begin{array}{l} \frac{\partial \eta}{\partial t}=-\frac{\partial(\eta u)}{\partial x}-\frac{\partial(\eta v)}{\partial y} \\ \frac{\partial u}{\partial t}=-v \frac{\partial u}{\partial y}-u \frac{\partial u}{\partial x}-g \frac{\partial \eta}{\partial x} \\ \frac{\partial v}{\partial t}=-u \frac{\partial v}{\partial x}-v \frac{\partial v}{\partial y}-g \frac{\partial \eta}{\partial y} \end{array}\right.\tag{3-34} ⎩ ⎨ ⎧∂t∂η=−∂x∂(ηu)−∂y∂(ηv)∂t∂u=−v∂y∂u−u∂x∂u−g∂x∂η∂t∂v=−u∂x∂v−v∂y∂v−g∂y∂η(3-34)
其中, η \eta η 代表水深, t t t 为时间, x x x 和 y y y 是水平面上的坐标, u 、 v u 、 v u、v 是 x x x 和 y y y 方向上的流速, g g g 为重力加速度。物理上,这个方程组描述了水波在浅水区域内的传播和运动。它假设水深相对于波长很小,即波长远大于水深,这样就可以近似将水流速度视为垂直于水深方向的,这被称为“浅水近似”。
在实际应用中,二维浅水方程组被广泛用于预测海洋和河流等水动力学现象。例如,可以用它来预测风浪的形成和演变,或者用它来优化海岸线防护结构的设计。
需要注意的是,二维浅水方程组是一种近似模型,它对真实的水动力学现象只能提供近似的描述,实际情况可能更加复杂。因此,在具体应用中,需要根据实际情况选择合适的模型并对其进行修正和调整。对方程组 (3-34) 的等号两边做 x − y x-y x−y 空间上的二维傅里叶变换, 得到偏微分方程组:
{ ∂ η ^ ^ ∂ t = − i k x F { F − 1 [ η ^ ^ ] F − 1 [ u ~ ^ ] } − i k y F { F − 1 [ η ~ ^ ] F − 1 [ v ^ ] } ∂ u ^ ^ ∂ t = − F { F − 1 [ v ^ ^ ] ⋅ F − 1 [ i k y u ^ ^ ] + F − 1 [ u ⃗ ^ ] ⋅ F − 1 [ i k x u ^ ] } − i g k x η ^ ^ ∂ v ^ ∂ t = − F { F − 1 [ u ^ ] ⋅ F − 1 [ i k x v ^ ] + F − 1 [ v ^ ] ⋅ F − 1 [ i k y v ^ ] } − i g k y η ^ ^ (3-35) \left\{\begin{array}{l} \frac{\partial \hat{\hat{\eta}}}{\partial t}=-\mathrm{i} k_x F\left\{F^{-1}[\hat{\hat{\eta}}] F^{-1}[\hat{\tilde{u}}]\right\}-\mathrm{i} k_y F\left\{F^{-1}[\hat{\tilde{\eta}}] F^{-1}[\hat{v}]\right\} \\ \frac{\partial \hat{\hat{u}}}{\partial t}=-F\left\{F^{-1}[\hat{\hat{v}}] \cdot F^{-1}\left[\mathrm{i} k_y \hat{\hat{u}}\right]+F^{-1}[\hat{\vec{u}}] \cdot F^{-1}\left[\mathrm{i} k_x \hat{u}\right]\right\}-\mathrm{i} g k_x \hat{\hat{\eta}} \\ \frac{\partial \hat{v}}{\partial t}=-F\left\{F^{-1}[\hat{u}] \cdot F^{-1}\left[\mathrm{i} k_x \hat{v}\right]+F^{-1}[\hat{v}] \cdot F^{-1}\left[\mathrm{i} k_y \hat{v}\right]\right\}-\mathrm{i} g k_y \hat{\hat{\eta}} \end{array}\right.\tag{3-35} ⎩ ⎨ ⎧∂t∂η^^=−ikxF{F−1[η^^]F−1[u~^]}−ikyF{F−1[η~^]F−1[v^]}∂t∂u^^=−F{F−1[v^^]⋅F−1[ikyu^^]+F−1[u^]⋅F−1[ikxu^]}−igkxη^^∂t∂v^=−F{F−1[u^]⋅F−1[ikxv^]+F−1[v^]⋅F−1[ikyv^]}−igkyη^^(3-35)
取 g = 1 g=1 g=1, 初始条件为 η ( x , y , 0 ) = 0.1 ⋅ exp ( − x 2 / 10 − y 2 / 10 ) + 0.1 \eta(x, y, 0)=0.1 \cdot \exp \left(-x^2 / 10-y^2 / 10\right)+0.1 η(x,y,0)=0.1⋅exp(−x2/10−y2/10)+0.1 和 u ( x , y , 0 ) = v ( x , y , 0 ) = 0 u(x, y, 0)=v(x, y, 0)=0 u(x,y,0)=v(x,y,0)=0, 用傅里叶谱方法计算上述方程的代码如下:
主程序代码:
clear all; close all;
L=40; N=64;
x=L/N*[-N/2:N/2-1]; y=x;
kx=2*pi/L*[0:N/2-1 -N/2:-1]; ky=kx;
[X,Y]=meshgrid(x,y);
[kX,kY]=meshgrid(kx,ky);
%初始条件
e=0.1*exp(-X.^2/10-Y.^2/10)+0.1;
et=fft2(e); ut=zeros(N^2,1); vt=zeros(N^2,1);
euvt=[et(:); ut; vt;];
%求解
t=[0 5 10 25]; g=1;
[t,euvtsol]=ode45('shallow_water',t,euvt,[],kX,kY,N,g);
%画图
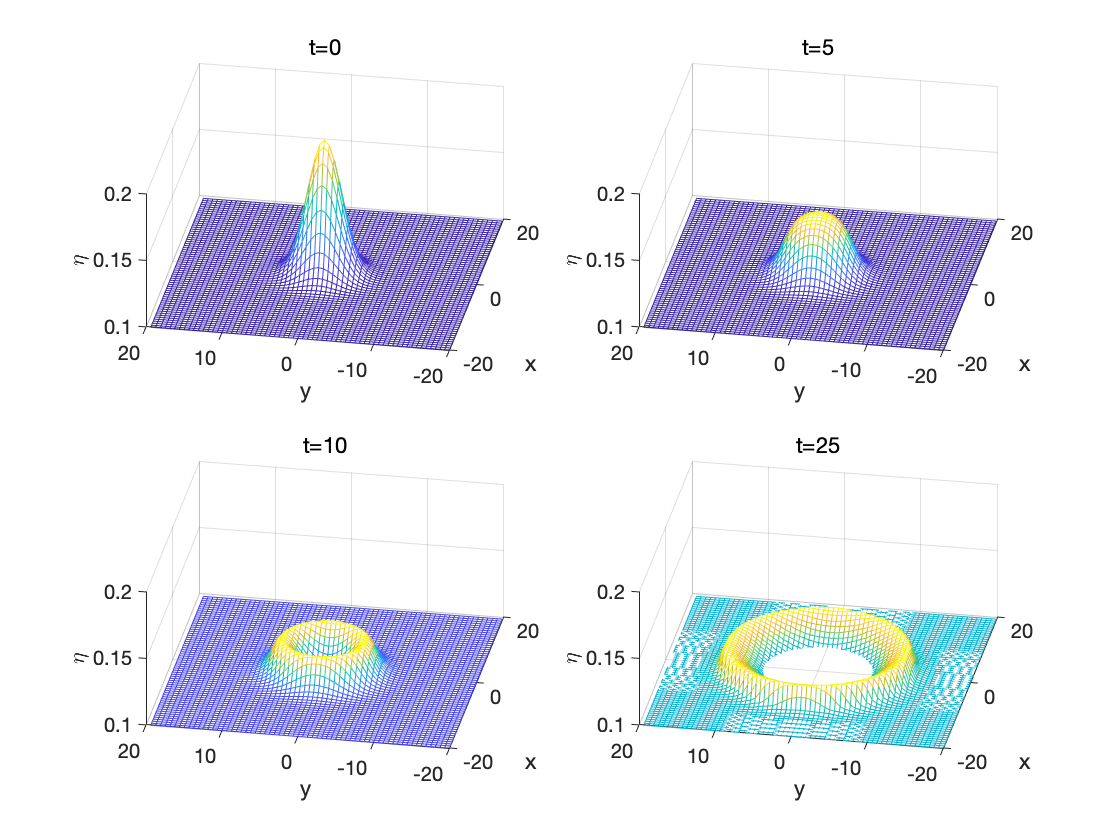
for n=1:4subplot(2,2,n)mesh(x,y,real(ifft2(reshape(euvtsol(n,1:N^2),N,N))))axis([-20 20 -20 20 0.1 0.2]), title(['t=' num2str(t(n))])xlabel x, ylabel y, zlabel \eta, view(-80,45)
end
程序输出结果如图所示, 从 t = 0 t=0 t=0 时刻开始, 一个三维高斯形水柱在重力的作用下坍塌, 并激起了向四周传播的圆形水波。
3.3.3 二维粘性 Burgers 方程
Burgers方程是一种非线性偏微分方程,它最初由荷兰数学家J. M. Burgers在20世纪30年代提出,用于描述一维粘性流体中的流动行为。
Burgers方程在物理学中具有广泛的应用。它可以用于模拟一维粘性流体中的多种现象,如激波、涡旋、湍流等。在流体力学中,Burgers方程常用于模拟流体中的湍流现象,如湍流尾流、湍流边界层等。在量子场论中,Burgers方程被用于描述费米子系统中的量子涡旋。
Burgers方程还是一些数值方法和数学工具的基础,如Shocks-capturing方法、Lax-Friedrichs格式等。这些方法可以有效地处理Burgers方程中出现的激波等非线性现象,从而得到比较精确的数值解。
Burgers方程也是非线性动力学中一个重要的模型。它的解可能会出现奇点和激波等非线性现象,这些现象为非线性偏微分方程的研究提供了新的思路和挑战。通过对Burgers方程的研究,可以深入了解非线性动力学中的一些重要现象和性质。
此外,Burgers方程还被应用于宏观经济学中的一些问题,如经济增长、通货膨胀等。通过对Burgers方程的应用,可以揭示一些经济现象的本质规律和机制。
除了上述介绍的应用和研究方向,Burgers方程还有以下一些特点和性质:
Burgers方程是一种具有非线性扰动传递性的方程。这意味着,当一个扰动在Burgers方程中传播时,它会不断地变形和扩散,从而形成复杂的结构。
Burgers方程可以通过一些数学方法和技巧来求解。其中比较常用的方法包括Burgers方程的相似变换、行波解法和反演公式等。
Burgers方程的解可能会出现激波、奇点等非线性现象。这些现象具有一定的物理意义,并且对于解决实际问题具有重要的作用。
Burgers方程可以被看作是Navier-Stokes方程的一维版本,它描述了粘性流体中的一些基本特性和行为。因此,Burgers方程在流体力学中有着重要的应用和研究价值。
Burgers方程还可以被拓展到更高维度或者更复杂的情形下。例如,二维Burgers方程、Burgers-Fisher方程等。
总之,Burgers方程在物理学、数学和工程学等领域具有广泛的应用和研究价值,它的研究和应用也带动了非线性动力学和偏微分方程等领域的发展。
Burgers 方程有钟行孤波和扭波两种形式的行波解(如图)
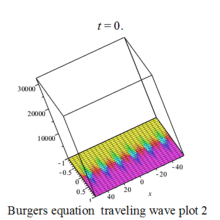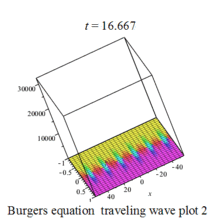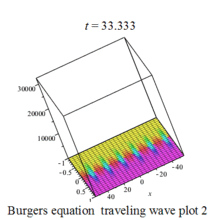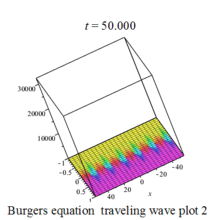
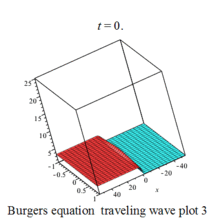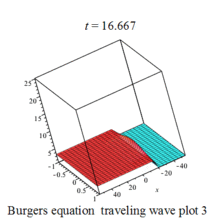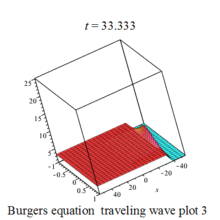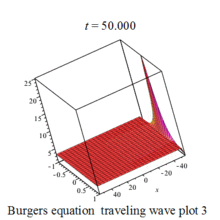
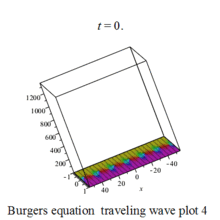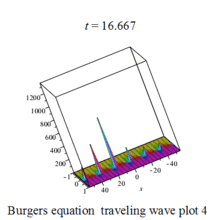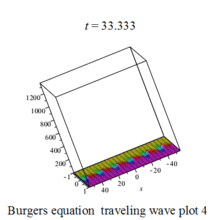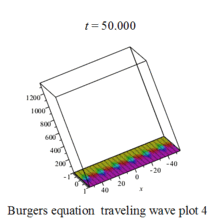
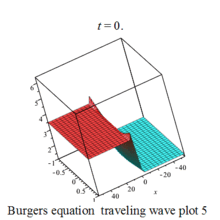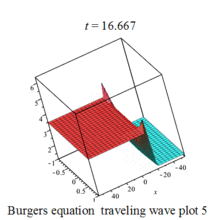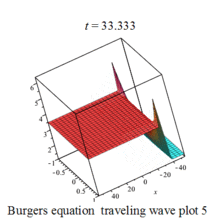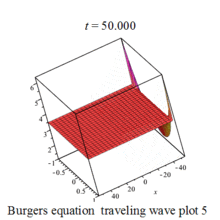
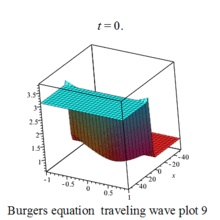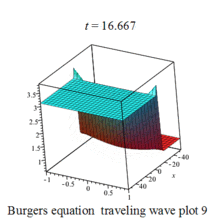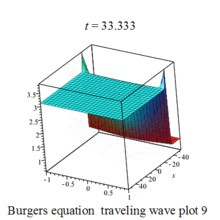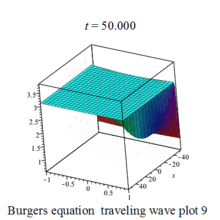
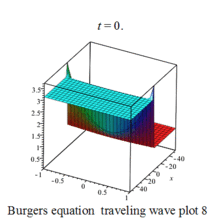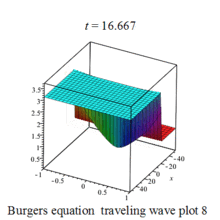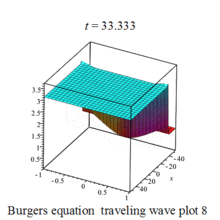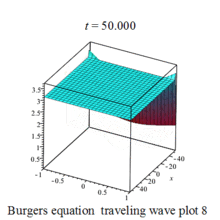
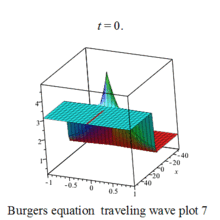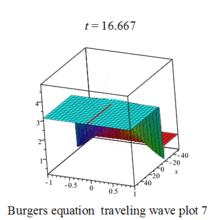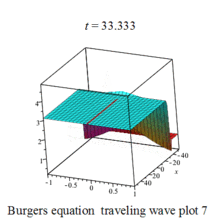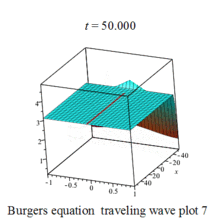
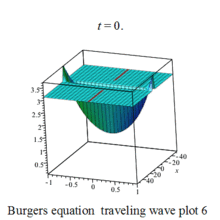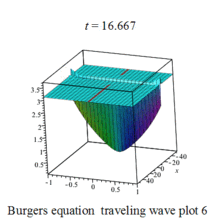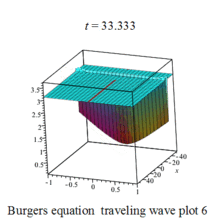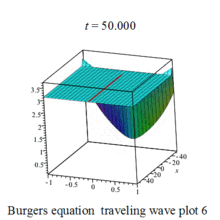
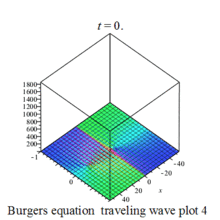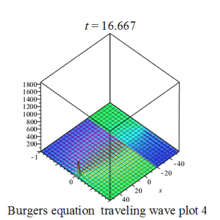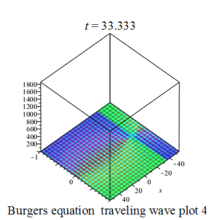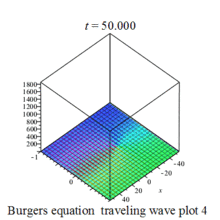
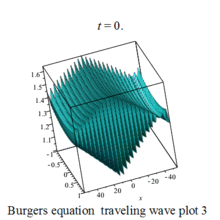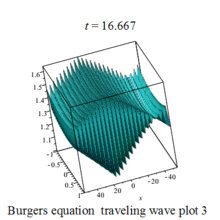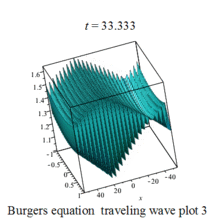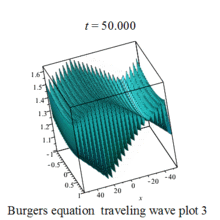
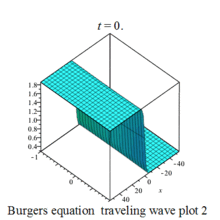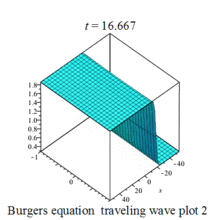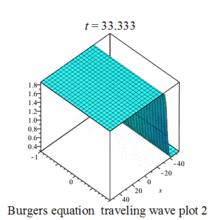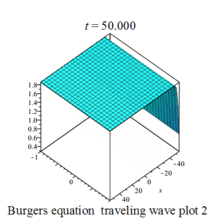
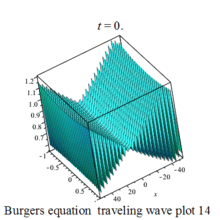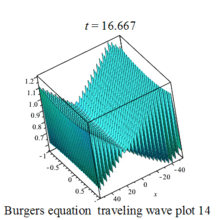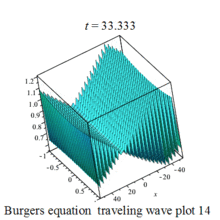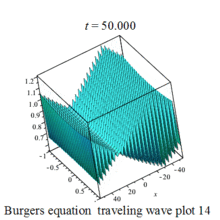
二维粘性 Burgers 方程的形式如下:
∂ u ∂ t = v ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 ) u − u ( ∂ ∂ x + ∂ ∂ y ) u (3-36) \frac{\partial u}{\partial t}=v\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u-u\left(\frac{\partial}{\partial x}+\frac{\partial}{\partial y}\right) u\tag{3-36} ∂t∂u=v(∂x2∂2+∂y2∂2)u−u(∂x∂+∂y∂)u(3-36)
其中, u u u 代表速度, x 、 y x 、 y x、y 为空间坐标, t t t 为时间, v v v 为粘性系数。对上式做二维傅里叶变换, 得:
∂ u ^ ^ ∂ t = − v ( k x 2 + k y 2 ) u ^ ^ − F { F − 1 [ u ^ ] ⋅ F − 1 [ i ( k x + k y ) u ^ ^ ] } (3-37) \frac{\partial \hat{\hat{u}}}{\partial t}=-v\left(k_x^2+k_y^2\right) \hat{\hat{u}}-F\left\{F^{-1}[\hat{u}] \cdot F^{-1}\left[\mathrm{i}\left(k_x+k_y\right) \hat{\hat{u}}\right]\right\}\tag{3-37} ∂t∂u^^=−v(kx2+ky2)u^^−F{F−1[u^]⋅F−1[i(kx+ky)u^^]}(3-37)
取 v = 0.01 v=0.01 v=0.01, 初始条件 u ( x , y , 0 ) = sech ( 4 x 2 + 4 y 2 ) u(x, y, 0)=\operatorname{sech}\left(4 x^2+4 y^2\right) u(x,y,0)=sech(4x2+4y2), 傅里叶谱方法的代码如下:
主程序代码:
clear all; close all;
L=4; N=64;
x=L/N*[-N/2:N/2-1]; y=x;
kx=2*pi/L*[0:N/2-1 -N/2:-1]; ky=kx;
[X,Y]=meshgrid(x,y);
[kX,kY]=meshgrid(kx,ky);
K2=kX.^2+kY.^2;
%初始条件
u=sech(4*X.^2+4*Y.^2);
ut=fft2(u);
%求解
v=0.01; t=0:0.4:1.2;
[t,utsol]=ode45('burgers',t,ut(:),[],N,kX,kY,K2,v);
%画图
for n=1:4subplot(2,2,n)mesh(x,y,real(ifft2(reshape(utsol(n,:),N,N))))axis([-2 2 -2 2 0 1]), xlabel x, ylabel y, zlabel uview(46,20), title(['t=' num2str(t(n))])
end
程序执行结果如图所示,初始波形逐渐演变成激波,这是符合实际情况的。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-L46WfgOw-1680611827553)(https://mweb-1307664364.cos.ap-chengdu.myqcloud.com/2023/04/04/untitled12.png)]
当Burgers方程中的初始波形是单峰的、集中在某一区域内的时候,它会随着时间的推移而逐渐演变成为一个激波。这个现象可以通过分析Burgers方程的解得到解释。
在初始时刻,Burgers方程的初始波形会随着时间的推移而扩散,并逐渐变得平缓。然而,由于Burgers方程是一个非线性方程,波形在演化过程中会发生非线性的相互作用,这些相互作用会导致波形逐渐变得不规则,并在某些区域内出现奇点。当波形的斜率超过一定阈值时,这些奇点会形成激波,即波形在激波前是平缓的,但在激波后却是陡峭的。
激波的形成可以用物理学中的震荡现象来解释。当初始波形逐渐演化为激波时,波前的部分会受到高压的压缩,而波后的部分则会受到低压的拉伸,这样就形成了一个压缩波和一个展开波,它们相互作用,最终形成了一个陡峭的激波。
总之,Burgers方程中的初始波形逐渐演变为激波的现象,是由于非线性相互作用导致的,它在物理学和工程学等领域中有着广泛的应用。
这篇关于傅里叶谱方法-傅里叶谱方法求解二维浅水方程组和二维粘性 Burgers 方程及其Matlab程序实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





