opencv学习笔记（十）：图像缩放、平移、旋转变换理论推导及应用

opencv学习笔记（十）：图像缩放、平移、旋转变换理论推导及应用

基础知识I——图像仿射变换

仿射变换包括如下所有变换，以及这些变换任意次序次数的组合：

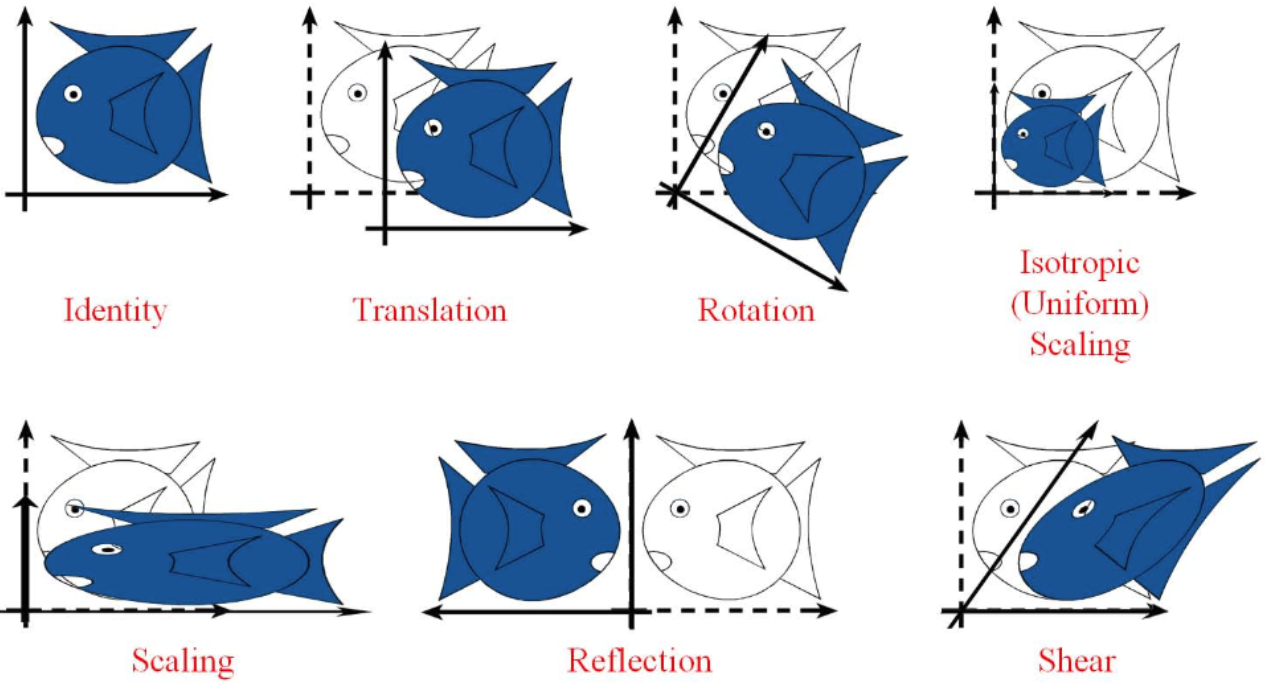
平移（translation）和旋转（rotation）顾名思义，两者的组合称之为欧式变换（Euclidean transformation）或刚体变换（rigid transformation）；

放缩（scaling）可进一步分为uniform scaling和non-uniform scaling，前者每个坐标轴放缩系数相同（各向同性），后者不同；如果放缩系数为负，则会叠加上反射（reflection）——reflection可以看成是特殊的scaling；

刚体变换+uniform scaling 称之为，相似变换（similarity transformation），即平移+旋转+各向同性的放缩；
剪切变换（shear mapping）将所有点沿某一指定方向成比例地平移。

上述变换都可以通过矩阵操作进行：
没有平移或者平移量为0的所有仿射变换可以用如下变换矩阵描述：

为了增添平移这一变换，变换矩阵写为：

基础知识II——图像插值算法

1.为什么会有图像插值的概念？

以小图像放大为大图像为例：

从上图可以看出，当一个小图像放大为大图像时，像素点的位置坐标随之变化，放大后的图像会存在像素缺失（图中橙色点所示），如果这些位置上的像素不做处理就会造成图像严重失真，为了解决这个问题，便有了图像内插问题的提出。

2.经典的图像插值算法

• 最近邻插值（Nearest）
• 双线性插值（Bilinear）
• 双三次插值（Bicubic）

最近邻插值（最简单的插值方法）

如上图所示，图2.1是原始图像，图2.2是图2.1放大2倍以后得到的图像，其像素点的横纵坐标均扩大为原来的两倍，那么会产生出其他位置的新像素，如图2.2中浅色圆圈所示。
最近邻插值是将图2.2中五个未知像素点横纵坐标缩小2倍，那么这5个像素点的位置一定落在图2.1中四个像素的四邻域内，对于一个未知像素的像素点来说，其像素值和离它最近的已知像素点的像素值相同。
最近邻插值简单便捷，其计算速度快，但是当一个图片需要放大较大倍数时，会出现马赛克现象。举个简单例子，当一个图像放大500倍时，此时两个原有像素点之间就存在499个待插值，那么必定会存在有连续位置上的像素值相同，这样就会出现马赛克现象。

双线性插值

双线性插值有前提假设：假设原图像的灰度是线性变化的。

如上图所示，假设代插点映射回原图的位置为$e(u,v)$,$u$ ,$v$显然都是非整数，$A$,$B$,$C$,$D$四点对应的灰度值分别为$I(i,j)$,$I(i,j+1)$,$I(i,j+1)$,$I(i+1,j+1)$。

• 要求出$e(u,v)$的像素值首先要求出$e_1(u,j)=e_1(i+d_x,j)$与$e_2(u,j+1)=e_2(i+d_x,j+d_y)$的像素值。
• x轴的单线性插值： 根据原图像灰度线性变化，可由$A$,$B$两点的像素值以及它们之间的线性关系求出$e_1$的像素值——$e_1(u,j)=d_x(I(i,j+1)-I(i,j))+I(i,j)$,同理可以求出$e_2$。
• y轴的单线性插值： 根据$e_1$与$e_2$两点的插值再次求线性插值即可。
  根据上述推导，双线性插值法其实是利用待插像素点四个邻接像素点的灰度值在水平和垂直方向上作线性内插，它的运算量要比最近邻域法复杂些，但克服了灰度不连续的缺点，整体视觉效果较好。同时需要注意到，它具有⭐️低通滤波⭐️的性质（该方法没有考虑图像灰度变化率的情况，只是根据位置来确定插值的像素权重，若两个像素点像素值分别为0、255，跨越了整个8bit灰度级的灰度范围，放大后这两点之间的坐标上将会填充一系列渐变的像素值，导致0、255的视觉跨度降低，也就导致某些图片上边缘模糊），图像的高频分量会在此插值过程中受损，导致效果图中的轮廓有一定的模糊，细节不够突出。

双三次插值

维基百科中对双三次插值的推导

---

缩放变换——resize函数

先展示一张较大图片

import cv2 
import numpy as npImg = cv2.imread ('1.png',cv2.IMREAD_UNCHANGED)
cv2.imshow('img',Img)
cv2.waitKey(0)

显示效果如下：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-md7uJpGj-1673570245578)(http://restar-xt.cn/wp-content/uploads/2023/01/Python显示过大图片.png)]
发现图片显示不全，那么可以通过缩放函数resize解决问题

函数原型

dst	=	cv.resize(	src, dsize[, dst[, fx[, fy[, interpolation]]]]	)
@参数：
src	  input image.输入图像
dst	  output image; it has the size dsize (when it is non-zero) or the size computed from src.size(), fx, and fy; the type of dst is the same as of src.输出图像
dsize	output image size; if it equals zero, it is computed as:
dsize = Size(round(fx*src.cols), round(fy*src.rows))
Either dsize or both fx and fy must be non-zero.输出图像的大小
fx	scale factor along the horizontal axis; when it equals 0, it is computed as
(double)dsize.width/src.cols  x轴缩放因子
fy	scale factor along the vertical axis; when it equals 0, it is computed as
(double)dsize.height/src.rows  y轴缩放因子
interpolation	interpolation method, see InterpolationFlags 插值方法

说明：对于插值方法，OpenCV提供了多种插值方法：

INTER_NEAREST	最近邻插值
INTER_LINEAR	双线性插值
INTER_CUBIC	双三次插值
INTER_AREA	区域插值
INTER_LANCZOS4	兰索斯插值

接下来将之前展示的图片进行缩小：

import cv2 
import numpy as npImg = cv2.imread ('1.png',cv2.IMREAD_UNCHANGED)
Img_1 = cv2.resize(Img,None,None,0.1,0.1,cv2.INTER_NEAREST)cv2.imshow('Original Image',Img)
cv2.imshow('Nearest Image',Img_1)cv2.waitKey(0)

运行结果如下：

在本文开头曾介绍了最近邻、双线性、双三次插值，为了更加清晰直观地说明三种插值方式的优劣性，以同样放大倍数放大同一图片进行观察：

import cv2 
import numpy as npImg = cv2.imread ('lena.png',cv2.IMREAD_UNCHANGED)
Img_1 = cv2.resize(Img,None,None,5,5,cv2.INTER_NEAREST)
Img_2 = cv2.resize(Img,None,None,5,5,cv2.INTER_LINEAR)
Img_3 = cv2.resize(Img,None,None,5,5,cv2.INTER_CUBIC)
cv2.imshow('Original Image',Img)
cv2.imshow('Nearest Image',Img_1)//最近邻插值
cv2.imshow('Linear Image',Img_2)//双线性插值
cv2.imshow('Cubic Image',Img_3)//双三次插值
cv2.waitKey(0)

运行结果如下：

可见左图（最近邻插值）方块（马赛克）情况严重，中图（双线性插值）与右图（双三次插值）在lena头发处对比明显，双三次插值放大的图像边缘更加平滑。

探究将一张图片缩小a倍，再将缩小后的图像放大a倍

注意：进行缩小处理时常用区域插值，进行放大处理时常用双线性插值或双三次插值。
代码如下：

import cv2 
import numpy as npImg = cv2.imread ('lena.png',cv2.IMREAD_UNCHANGED)
Img_1=cv2.resize(Img,None,None,0.5,0.5,cv2.INTER_AREA)
Img_2=cv2.resize(Img_1,None,None,2,2,cv2.INTER_CUBIC)
cv2.imshow('Original Image',Img)
cv2.imshow('Smaller Image',Img_2)
cv2.waitKey(0)

运行结果如下：主要比较缩小再放大的图像与原图的区别。

从上图可看出，左图作为缩小后又放大的图像明显具有模糊（马赛克）效果，这是由于缩小时本身会损失一部分像素值，放大以后的图像这部分像素值缺失，是通过插值来填充的，为了解决缺失像素点恢复的问题可以通过图像金字塔等相关知识解决。

写在前面：接下来的平移变换和旋转变换其实都属于仿射变换，它们可以用变换矩阵达到目的，故二者使用的核心函数都是warpAffine函数，只不过平移变换的变换矩阵很简单容易求出，而且平移变换只涉及水平、竖直两个方向；而旋转变换则涉及旋转中心、旋转角度等，其对应的变换矩阵无法一眼求出，需要借助相关函数，这就是二者在使用过程中的区别。

平移变换——warpAffine函数

平移变换是矩阵操作，对图像进行矩阵操作主要有两步：

• 构建对应矩阵
• 进行矩阵乘法

一般使用Numpy模块来构建矩阵，矩阵数据类型为单精度浮点数float32（这是由OpenCV函数参数决定的）。

函数原型

dst	=	cv.warpAffine(	src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]	)
@参数说明：
@src	  input image.输入图像
@dst	  output image that has the size dsize and the same type as src .输出图像
@M	    2×3 transformation matrix.2*3的矩阵
@dsize	size of the output image.输出图像大小
@flags	combination of interpolation methods (see InterpolationFlags) and the optional flag WARP_INVERSE_MAP that means that M is the inverse transformation ( dst→src ).插值方法，可选参数WARP_INVERSE_MAP表示图像逆变换——dst->src
@borderMode	pixel extrapolation method (see BorderTypes); when borderMode=BORDER_TRANSPARENT, it means that the pixels in the destination image corresponding to the "outliers" in the source image are not modified by the function.像素外推方法
@borderValue	value used in case of a constant border; by default, it is 0.固定边框

关于函数中M矩阵的推导，为什么是2*3矩阵?
设图像中一个像素(像素坐标)的向量（矩阵）表示为:

变换矩阵为：

两个矩阵相乘：

这样就实现了像素点的平移，对原图像所有像素点做如此处理即可得到原图像平移。

实现一幅图像的平移

import numpy as np
import cv2Img = cv2.imread('lena.png',cv2.IMREAD_UNCHANGED);
M=np.float32([[1,0,50],[0,1,50]])#创造2*3矩阵，与上文推导对比可知，该矩阵可使图片沿x轴、y轴均平移50个单位长度
ImgTranslation = cv2.warpAffine(Img,M,(Img.shape[0],Img.shape[1]))
cv2.imshow('ImgTranslation',ImgTranslation)
cv2.imshow('Original',Img)
cv2.waitKey(0)

运行效果如下：

产生的黑色边框是由于平移后像素点填充为$（0,0,0）$造成的。

旋转变换——warpAffine函数

原理推导

情况1：绕原点旋转

设$P(x,y)$是原始坐标，$Q(x,y)$是$P$点旋转一定角度得到的点，先求$Q$点由$P$点坐标表出的坐标表示：
$x^{,}=D\cos (\alpha +\beta )=D(\cos \alpha \cos \beta -\sin \alpha \sin \beta )=x\cos \beta -y\sin \beta$
$y^{,}=D\sin (\alpha +\beta )=D(\sin \alpha \cos \beta +\cos \alpha \sin \beta )=y\cos \beta +x\sin \beta =x\sin \beta +y\cos \beta$
将上述两式用矩阵表示：

情况2：绕任意点旋转

点绕任意中心位置旋转其实就是先将坐标系从原点位置平移后旋转再平移回来。
该旋转矩阵较情况1来说复杂一些，但是OpenCV库内置了getRotationMatrix2D函数可以方便快捷地求出旋转矩阵。

opencv的getRotationMatrix2D函数可以获取旋转变换矩阵。输入中心点坐标(centerX,centerY)，旋转角度θ，缩放比例，给出M变换矩阵：

M变换矩阵推导如下：

• 首先用矩阵表示某一像素点$A(x,y)$：

• 围绕任意点旋转其实就是把原图原点先平移到任意点，旋转相应角度后再平移回来。
• 假设任意点坐标为$B(mx,ny)$,将原点$(0,0)$平移到$B$点,其实相当于把$A$点进行同样的平移操作：

• 此时旋转中心就是新的“原点”，下面将$M$矩阵做旋转变换：

• 旋转操作完成后，即可将当前图像重新平移回去：

• 化简$Y$中的变换矩阵可得：

函数原型

warpAffine函数的函数原型见上文。
着重介绍getRotationMatrix2D函数的使用。

retval	=	cv.getRotationMatrix2D(	center, angle, scale	)
@参数说明：
@center	Center of the rotation in the source image.选定的旋转中心
@angle	Rotation angle in degrees. Positive values mean counter-clockwise rotation (the coordinate origin is assumed to be the top-left corner).旋转角度（正值意味着顺时针旋转）
@scale	Isotropic scale factor.比例各向同性比例因子。

实现一幅图像的旋转

import numpy as np
import cv2Img = cv2.imread('T.jpg',cv2.IMREAD_UNCHANGED);
M=cv2.getRotationMatrix2D((145,420),-5,1)
ImgRotation = cv2.warpAffine(Img,M,(Img.shape[0],Img.shape[1]))
cv2.imshow('ImgRotation',ImgRotation)
cv2.namedWindow('ImgRotation',1)
cv2.resizeWindow('ImgRotation',3*Img.shape[0],3*Img.shape[1])
cv2.imshow('Original',Img)
cv2.waitKey(0)

运行效果如下：

注意到平移和旋转处理后图像都没有完全地显示出来（有黑边），故以旋转为例，尝试写出一套实现图像无损旋转的算法。

实现图像绕中心点无损旋转

理论推导

由上文推导可知，变换矩阵$\Gamma$如下：

现在假设存在一幅图像经过相应旋转变换，原图与旋转后的图相对位置关系如下图所示：

要使新图像能够完全显示，那么画布的长一定大于等于两条蓝线长度之和，画布的宽一定大于等于两条红线长度之和，设原图像高为$h(rows)$，宽为$w(cols)$，则用数学公式表达有：

上述两式中旋转角$\beta$均为弧度制，但在编程中，我们并非常常使用弧度制，故还有以下表达：

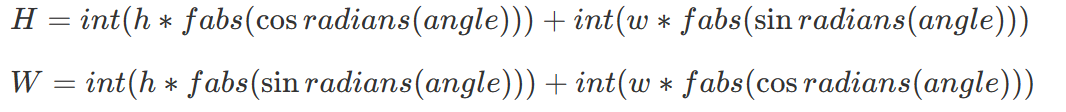
注意：新的画布扩大是基于原图左上角点（原点）扩大，显示区域同样丢失了信息.

下一步，需要将画布按照旋转点位置进行平移（类比上文中绕任意点旋转等于平移再旋转再逆平移的原理），如下图所示，要将画布从蓝色区域平移至红色区域，但OpenCV的画布没有办法平移，只是由输入图像的大小决定，因此我们可以通过将图像平移回原来的位置进行解决，可以更改矩阵$M$的平移决定值：

代码如下：

import math
import cmath
import cv2
import numpy as npdef opencv_rotate(img, angle):h, w = img.shape[:2]center = (w / 2, h / 2)scale = 1.0# 2.1获取M矩阵M = cv2.getRotationMatrix2D(center, angle, scale)# 2.2 新的宽高，radians(angle) 把角度转为弧度 sin(弧度)new_H = int(w * abs(math.sin(math.radians(angle))) + h * abs(math.cos(math.radians(angle))))new_W = int(h * abs(math.sin(math.radians(angle))) + w * abs(math.cos(math.radians(angle))))# 2.3 平移M[0, 2] += (new_W - w) / 2M[1, 2] += (new_H - h) / 2rotate = cv2.warpAffine(img, M, (new_W, new_H),flags = cv2.INTER_CUBIC borderValue=(255, 255, 255))return rotateIMG = cv2.imread('T.jpg',cv2.IMREAD_UNCHANGED)
opencv_rotate(IMG,60)
cv2.imshow('Rotation',opencv_rotate(IMG,90)) 
cv2.waitKey(0)

运行结果如下：

图片旋转中也涉及到图像插值的问题（可参考冈萨雷斯《数字图像处理》（第三版）第二章图像旋转部分的例子展示），插值方式对旋转变换后图像直边缘的保持具有重要作用。以下图片从左到右依次是上述代码采用最近邻、双线性、双三次插值得到的"T"字母直边缘放大1000倍的图像：

仿射变换

仿射变换是在旋转变换以及平移变换的基础上得来的。
旋转变换和平移变换不会改变输入图像的形状，即使可以通过调整缩放因子来控制输出图像的大小，但是最后的输出图像与输入图像之间没有形状上的差异，这种变换称为刚性变换。
而仿射变换并非刚性变换，它会造成图像的改变，但是并非完全无规则的改变。有以下特征：

• 平直性：直线变换过后依然是直线。
• 平行性：二维图形之间的相对位置关系保持不变，平行线依然是平行线，且直线上点的位置顺序不变。
  仿射变换可以写成如下形式：

$$\{\begin{array}{ll}{x}^{,}=ax+by+m& \\ y^{,}=cx+dy+n& \end{array}$$

注意到上述方程组中含有6个未知数，需要6个方程构成齐次方程组进行求解，要使方程有唯一解，必须要求这三个点不在同一直线上！因此，常说三个点确定唯一的仿射变换。

放射变换的变换矩阵推导

较简单，不再赘述：

函数原型

这里介绍的函数是求解仿射变换变换矩阵的函数——cv2.getAffineTransform(src,dst)

retval	=	cv.getAffineTransform(	src, dst	)
@参数说明：
@src	Coordinates of triangle vertices in the source image.源图像中三角形顶点的坐标。@dst	Coordinates of the corresponding triangle vertices in the destination image.目标图像中相应三角形顶点的坐标。

实现仿射变换

import numpy as np
import cv2
#读取图片
Img = cv2.imread('T.jpg',cv2.IMREAD_UNCHANGED);
#获取图片大小
rows = Img.shape[0]
cols = Img.shape[1]
#创建原图三角点与目标图像三角点
Oritriangle = np.float32([[20,20],[20,30],[60,25]])
Afftriangle = np.float32([[20,20],[20,30],[60,10]])
#计算变换矩阵
M = cv2.getAffineTransform(Oritriangle,Afftriangle)
#实现仿射变换
Img_Aff = cv2.warpAffine(Img,M,(cols,rows),flags=cv2.INTER_CUBIC)
#展示原图与变换后图像并对比
cv2.imshow('Img_Aff',Img_Aff)
cv2.imshow('Img',Img)
cv2.waitKey(0)

运行结果如下：

透视变换——在车道线检测上的应用

见下一次笔记