本文主要是介绍2018年亚太杯APMCM数学建模大赛A题老年人平衡能力的实时训练模型求解全过程文档及程序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2018年亚太杯APMCM数学建模大赛
A题 老年人平衡能力的实时训练模型
原题再现
跌倒在老年人中很常见。跌倒可能会导致老年人出现许多并发症,因为他们的康复能力通常较差,因此副作用可能会使人衰弱,从而加速身体衰竭。此外,对跌倒的恐惧可能会削弱行动能力,限制行动范围,从而显著恶化生活质量。因此,对老年人进行平衡能力评估,以帮助他们改善行动状态、纠正姿势和防止意外跌倒,具有重要的现实意义。
目前还没有一个包罗万象的平衡定义。在医学中,平衡有两层含义。一种是当人体保持稳定姿势时的静态平衡状态。另一种是当身体在运动或受到外力时,自动调整自己以保持姿势时的动态平衡状态。在力学中,当物体上的合力为零时,就会产生平衡。身体的平衡或稳定性与重心的位置和支承面的面积有关。如果重心线落在轴承表面内,或者发生不平衡,则保持机体平衡。
一家研究机构通过在老年受试者身上部署42个监测点进行了随机抽样测试。见下图所示各点的布局。
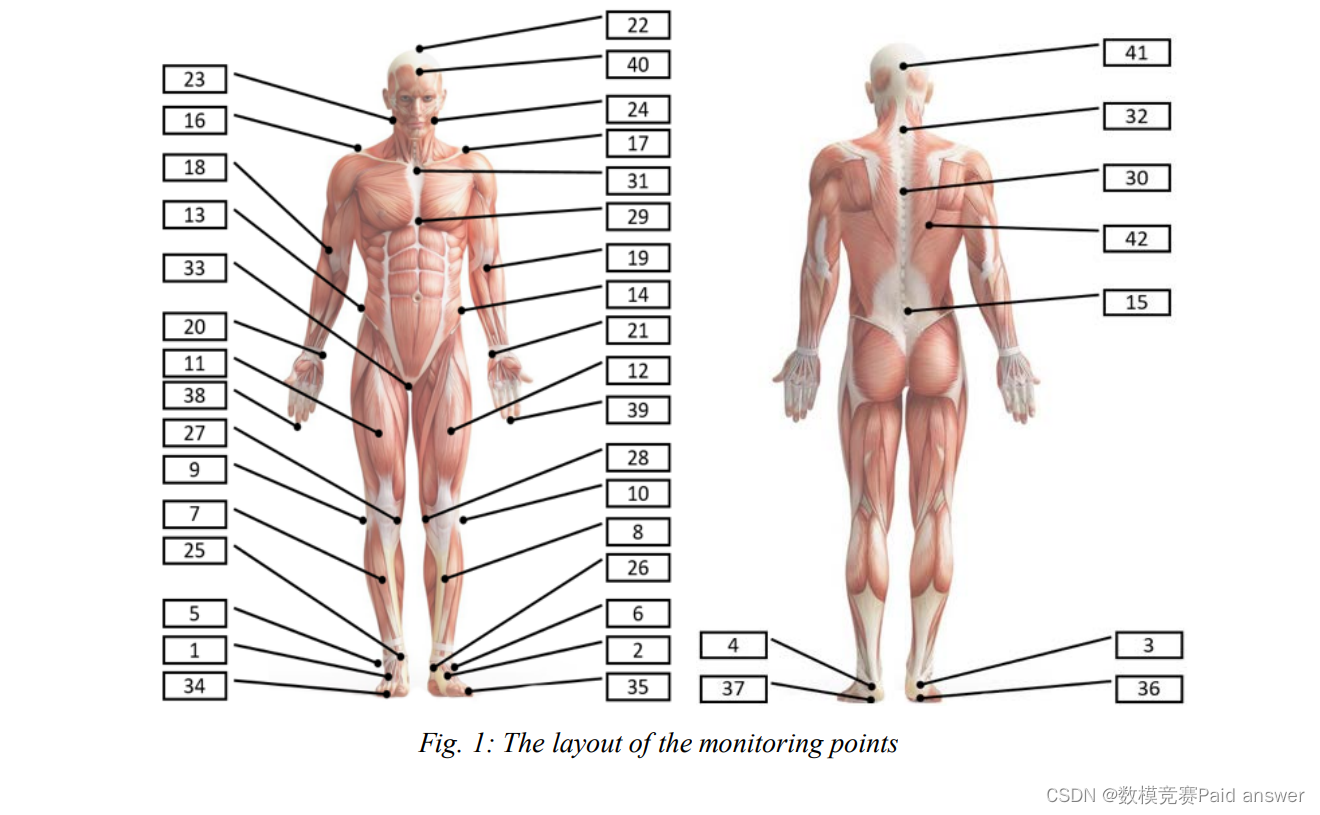
根据附件中的实验数据,完成以下任务:
问题1:根据附件2中的数据分析老年人的平衡特征。基于对步数、重心和运动的分析,建立特征提取模型。应用由42个监测点组成的系统提取25个身体平衡特征,对老年人的身体平衡进行综合评估。
问题2:建立基于25个指标的平衡风险评估体系,评估老年人的平衡能力。给出相应的建议。
问题3:根据提供的实际数据,对身体平衡力进行模拟计算和比较分析。为平衡能力较弱的老年人提供有效的建议。
附件说明:
附件1:《老年人基本数据》(格式:.xlsx)包含所有老年受试者的基本数据。
附件2:附件2包含每个受试者在自由行走状态下的校准原始数据。有三个完整的gait(文件后缀:.trc),可以用Excel打开。第一列是帧序列,第二列是时间。从第三列开始,每三列代表监测点的运动坐标(x,y,z)。共有42个监测点。
整体求解过程概述(摘要)
跌倒会造成成吨的伤害,这将影响老年人的生活水平。因此,结合步行时的身体姿势等因素,为他们建立一个平衡能力评估体系具有重要意义。
我们的模型首先采用R型聚类方法和马氏距离从42个监测点中提取出25个具有医学意义的指标。我们的25项指标包含90.86%的全身特征信息,可靠性高。这一结果使测量每个受试者的基本身体状况成为可能。
然后,基于这25个指标,采用改进的多项式曲线拟合方法建立了一个平衡能力体系,并将稳定配速曲线与实验配速曲线进行了比较,以塑造一个人的平衡能力。然后,我们的研究将我们的结果与实际跌倒时间进行了比较,对于所有有跌倒风险的老年人来说,准确率达到了近80%。然而,当应用于中等风险的老年人时,准确性会迅速下降。由于这种现象,我们的模型做了更多的改进。
在我们改进的评估系统中,我们的模型考虑了TOPSIS的实际数据。我们使用来自实际数据的7个参数和附录2的追踪数据来衡量老年人的平衡能力。与实际跌倒时间相比,我们在几乎所有老年人中获得了80%的准确率。此外,我们改进的评估可以从整体上划分出平衡能力高和平衡能力低的老年人。
改进模型的敏感性分析表明,模型中年龄和BMI参数的微小变化对结果的影响较小。3%的干扰只会影响2.5%的排名,5%的干扰会影响7.5%的排名。最后,我们从医学角度对不同类型的跌倒或平衡能力低下的老年人提出了不同的建议。
模型假设:
1.记录跟踪数据时没有时间差。
2.25个指标具有医学意义和物理意义,能够预测重心等物理参数。
3.跟踪数据能够预测平衡能力。由于我们的R-TYPE CLUSTER算法、PCA算法都是基于实际数据的。
4.追踪数据是每个受试者的正常步骤,即每个人在实验室里都像平时一样行走,尤其是在摔倒前。
5.在长者跌倒和被追踪的这些年里,身体没有发生大的变化。
问题重述:
背景
在过去的几十年里,我国的老龄化程度逐渐加快。预计到2050年,60岁以上人口将占总人口的33%。这些年来,老年人摔倒事故也在大规模增加。当老年人跌倒时,他们会不稳定,失去平衡,对老年人来说,下半身肌肉衰退会导致平衡能力下降,不足以支撑老年人在跌倒时下半身;同时,由于老年人神经系统控制能力下降,神经传导减慢,运动反应时间延长,也会导致老年人在跌倒时不能及时调整身体保持平衡。这样,就有必要衡量老年人的平衡能力,为他们提供适当的建议,让他们保持平衡,更加注意他们的平衡。
此外,对老年人平衡能力的预测研究较少。此外,大多使用单个传感器,检测精度有限,容易误判。
问题重述
建立一个模型,其中包含来自给定42个监测点的25个主要指标。该模型需要用于分析每个受试者的步数、重心、速度和加速度等。
根据实际实验数据,建立一个能够评估老年人平衡能力的模型。
模拟那些几年前摔倒的老年人,并向我们的模型证明我们的模型是否能够监测他们的平衡能力。
为那些平衡能力较弱的老年人提供建议。
模型的建立与求解整体论文缩略图


全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
%% import dataresultvar_yy=[];resultvar_zz=[];A = dir(fullfile('*.trc'));
for iiii=1:1:76data1=load(A(iiii).name);result_yy=[];result_zz=[]; resultfit_yy=[];resultfit_zz=[]; data2=data1(:,3:end);%matrix1*126 for i=1:1:25%rowyy=[];zz=[];for ii=2:1:5%columnif data3(i,ii)~=0yy=[yy,data2(:,3*data3(i,ii)-1)];zz=[zz,data2(:,3*data3(i,ii))];endendresult_yy=[result_yy,mean(yy,2)];result_zz=[result_zz,mean(zz,2)];yytofit=result_yy(:,i);zztofit=result_zz(:,i);% Create the model.fun = @(x,xdata)x(1)+x(2)*xdata+x(3)*(xdata).^2+x(4)*(xdata).^3 +x(5)*
(xdata).^4 +x(6)*(xdata).^5+x(7)*(xdata).^6+x(8)*(xdata).^7;tdata =data1(:,2);m0 = 1.0e+04 *[0.0280 0.1155 -0.6000 1.1672 -1.1046
0.5433 -0.1334 0.0129];% Solve the bounded fitting problem.my1 = lsqcurvefit(fun,m0,tdata,yytofit);my2 = lsqcurvefit(fun,my1,tdata,yytofit);yyfitted=fun(my2,tdata);mz1 = lsqcurvefit(fun,m0,tdata,zztofit);mz2 = lsqcurvefit(fun,mz1,tdata,zztofit);
zzfitted=fun(mz2,tdata);resultfit_yy=[resultfit_yy,yyfitted];resultfit_zz=[resultfit_zz,zzfitted]; difference_yy=abs(resultfit_yy-result_yy);difference_zz=abs(resultfit_zz-result_zz);var_yy=var(difference_yy,0,1);var_zz=var(difference_zz,0,1);endresultvar_yy=[resultvar_yy;var_yy];resultvar_zz=[resultvar_zz;var_zz];
end
%%CLUSTER
clc, clear all
%read in circle
A = dir(fullfile('*.trc'));
resultfinal=[];
for i=1:1:2data1=load(A(i).name);[m,n]=size(data1);a=[]; for ii=1:1:42X=[data1(:,3*ii+1),data1(:,3*ii+2)];a(:,ii)=pdist(X,'mahal');end%%b=zscore(a); %standard the datar=corrcoef(b); %coefficient matrixd=pdist(b','correlation'); %计算相关系数导出的距离z=linkage(d,'average'); %按类平均法聚类figureh=dendrogram(z); %画聚类图set(h,'Color','k','LineWidth',1.3) %把聚类图线的颜色改成黑色,线宽加粗
T=cluster(z,'maxclust',25); %cluster into 25 catagoryresults= [];for iii=1:25tm=find(T==iii); %find the ith coatogory’s subjetcttm=reshape(tm,1,length(tm)); %in row
results=[results;tm,zeros(1,15-length(tm))];end resultfinal=[resultfinal;results];end
%% topsis
clc, clear
data=load('datatopsis.txt');
[m,n]=size(data);
fun=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb &
x<qujian(1))+(x>=qujian(1) & x<=qujian(2))+(1-(x-qujian(2))./(ubqujian(2))).*(x>qujian(2) & x<=ub);
%properties trans
qj2=[0.41,0.48]; lb2=0.35; ub2=0.52;
data(:,2)=fun(qj2,lb2,ub2,data(:,2));
qj3=[2.5,5]; lb3=2; ub3=5.8;
data(:,3)=fun(qj3,lb3,ub3,data(:,3));
qj6=[19,28]; lb6=17; ub6=32;
data(:,6)=fun(qj6,lb6,ub6,data(:,6));
for j=1:nb(:,j)=data(:,j)/norm(data(:,j)); % normalize the matrix
end
%% weight
% data analysis in 1
maxdata=repmat(max(data),m,1);
mindata=repmat(min(data),m,1);
max_min=maxdata-mindata;
stddata=(data-mindata)./max_min;
%calculatee the weight
f=(1+stddata)./repmat(sum(1+stddata),m,1);
e=-1/log(m)*sum(f.*log(f));
d=1-e;
w=d/sum(d); % 权重向量
%%
c=b.*repmat(w,m,1); %求加权矩阵
Cstar=max(c) %求正理想解
Cstar(1)=min(c(:,1)); Cstar(4)=min(c(:,4));
Cstar(5)=min(c(:,5));
Cstar(7)=max(c(:,7)); %属性 1,3,5,6 为成本型, 属性 2 为效益型
C0=min(c) %q 求负理想解
C0(1)=max(c(:,1)); C0(4)=max(c(:,4));
C0(5)=max(c(:,5));
C0(7)=min(c(:,7)); %属性 1,3,5,6 为成本型, 属性 8 为效益型
for i=1:mSstar(i)=norm(c(i,:)-Cstar); %求到正理想解的距离S0(i)=norm(c(i,:)-C0); %求到负理想的距离
end
f=S0./(Sstar+S0);
[sf,ind]=sort(f,'descend'); %求排序结果
Y=[ind',sf'];
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
这篇关于2018年亚太杯APMCM数学建模大赛A题老年人平衡能力的实时训练模型求解全过程文档及程序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







