本文主要是介绍神经网络 mse一直不变_神经网络法预测喷雾液滴尺寸的粗浅尝试,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
喷雾场中,液体射流受到气动力、表面张力、粘性力及自身惯性等多种因素之间复杂的相互作用破碎成液带、液块或液滴,而这些初次雾化的产物又会继续破碎成更小的液滴完成二次雾化,因此准确地预测喷雾场中液滴的尺寸及分布一直是困扰诸多研究者的难题。对于特定喷嘴,相较于实验及数值手段,采用理论方法能够更经济快捷地对雾化场特征进行预测,从而减少设计喷嘴的预算成本及时间。

图1 几种典型的初始雾化模型及液滴的二次雾化:(a)圆柱射流[1](b)锥形液膜[2](c)平面液膜[3](d)液滴破碎[4]
近年来在学术杂志上比较多见的理论预测液滴尺寸的方法是亚利桑那州立大学的Taewoo Lee使用的“基于控制体守恒方程的积分形式”方法[5-9]及本课题组根据Mayer[10]的全波假设发展的全波长积分方法[11-13]。
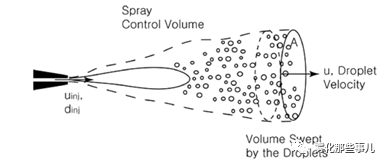
图2 T.-W Lee等人使用的基于控制体守恒方程的积分形式方法所选取的控制体。控制体入口为喷注平面,出口为液滴尺寸达到均匀状态的平面。图片来源:参考文献[7]Fig.1
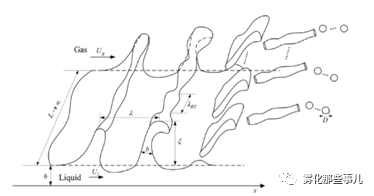
图3 L. Yang课题组根据Mayer[10]全波假设思想建立各种形式的液体射流雾化模型。图为高速气流下液膜的破裂过程。图片来源:参考文献[12]Fig.2
但以上的这两种方法得到的都是所谓“全场”概念的液滴尺寸,无法得到确切位置上液滴的尺寸。前段时间在偶然的查阅文献中,笔者发现使用神经网络法可对液滴尺寸进行相当好的预测,遂心驰神往。
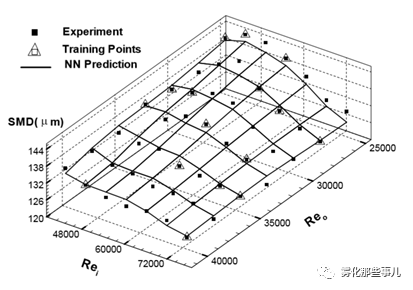
图4使用神经网络方法对液液同轴旋流喷嘴不同内外路射流Re数条件下液滴SMD的预测。图片来源:参考文献[14]Fig.5(b)
基于前人使用神经网络法对流场特征的预测研究,非常“投机”地针对性学习了BP、RBF和GRNN三种典型的神经网络,并尝试对文献中的实验数据进行了预测。
首先,择取Im等人[15]的实验数据,如图5所示。

图5气体中心式同轴旋流喷嘴不同径向位置处液滴SMD的实验测量。每条曲线代表不同的缩进比(RR为内喷嘴的无量纲缩进长度)。图中的条件为液体雷诺数Rel=587,气液动量比J=50,测量平面距离喷嘴出口z=3cm。图片来源:参考文献[15]Fig.15
提取出每个SMD值所对应的径向位置及RR值,得到储存径向位置及RR值的一个63*2数组和一个只储存SMD数据的63*1数组,分别命名为Input_set与Output_set,即为神经网络的训练输入与训练输出。将GRNN网络学习的经典案例:货运量预测[16]的程序做稍许改动,即可得到图6所示的预测结果。

图6 使用K折交叉验证的GRNN方法预测液滴尺寸。图中黑色立方体表示训练网络的实验数据,红色立方体表示选取用于预测的实验数据,红色球体表示网络的预测结果
在这里是随机选取了55组数据训练网络,剩余8组数据用来预测数据。因为对训练集和验证集的划分是随机的,所以每次运行出的结果是不相同的,但均可以保证误差小于±30%。这里所展现的是对程序数次运行后得到的较好的一个结果。图7所表示的是这8个预测值与实验数据之间的相对误差。在这里最大相对误差为-5.92%。
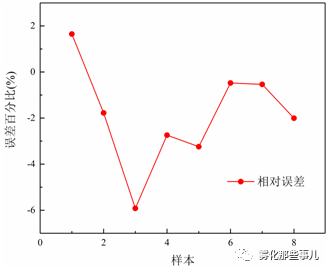
图7 GRNN预测值与实验数据的相对误差
在这里笔者进行的只是神经网络用于预测液滴尺寸的一个非常粗浅的尝试。大家有什么建议欢迎在评论区留言,您的每一条评论我们都会虚心接受并学习。
附:MATLAB程序
clear;clc;%celarvariables
nntwarn off % turn off neural network toolbox warnings
load('2010-JPP.mat') %load experimental data
%divide data intotraining and prediction categories
se=rand(1,63);
[m_se,n_se]=sort(se);
%training set
p_train=Input_set(n_se(1:55),:);%input
t_train=Output_set(n_se(1:55));%expectedoutput
%prediction set
p_test=Input_set(n_se(56:63),:);%input
t_test=Output_set(n_se(56:63));%expectedoutput
%cross-validation
desired_spread=[];%emptymatrix to store the most suitable spread value
mse_max=10e20;%maximumvalue for mse
desired_input=[];
desired_output=[];
result_perfp=[];
indices=crossvalind('Kfold',length(p_train),5);%dividedinto 5 groups
k=1;
for i=1:5
perfp=[];
test=(indices==i);
train=~test;
p_cv_train=p_train(train,:);
t_cv_train=t_train(train);
p_cv_test=p_train(test,:);
t_cv_test=t_train(test);
p_cv_train=p_cv_train';
t_cv_train=t_cv_train';
p_cv_test=p_cv_test';
t_cv_test=t_cv_test';
%normalized training data
[p_cv_train,minp,maxp,t_cv_train,mint,maxt]=premnmx(p_cv_train,t_cv_train);
p_cv_test=tramnmx(p_cv_test,minp,maxp);
for spread=0.1:0.1:2 %find suitable spreadvalue
%establish GRNN neural network
net=newgrnn(p_cv_train,t_cv_train,spread);
%get the output of the training process
test_Out=sim(net,p_cv_test);
%denormalized the output
test_Out=postmnmx(test_Out,mint,maxt);
%get the error between the expectedoutput and the training output
error=t_cv_test-test_Out;
disp(['当前网络的mse为',num2str(mse(error))])
perfp=[perfp mse(error)];
if mse(error)
mse_max=mse(error);
desired_spread=spread;
desired_input=p_cv_train;
desired_output=t_cv_train;
end
end
result_perfp(i,:)=perfp;
end
disp(['最佳spread值为',num2str(desired_spread)])%showthe optimum spread value
%adopt the optimumspread value to establish GRNN
net=newgrnn(desired_input,desired_output,desired_spread);
p_test=p_test';
p_test=tramnmx(p_test,minp,maxp);
grnn_prediction_result=sim(net,p_test);
grnn_prediction_result=postmnmx(grnn_prediction_result,mint,maxt);
grnn_error=(t_test-grnn_prediction_result');
%display predictedresults
figure(1)
plot(t_test,':og','LineWidth',2)
hold on
plot(grnn_prediction_result,'b-','LineWidth',2)
figure(2)
plot(grnn_error./grnn_prediction_result','ko','MarkerFaceColor','k');
title('神经网络预测误差百分比')
参考文献
[1] J. W. Hoyt, et al. Waves onwater jets[J]. Journal of Fluid Mechanics, 1977.
[2] Q. Fu, F. Ge, W. Wang et al.Spray characteristics of gel propellants in an open-end swirl injector[J].Fuel, vol. 254, 2019, 115555
[3] V. Sivadas, E. C. Fernandes, M.V. Heitor. Acoustically excited air-assisted liquid sheets[J]. Experiments inFluids, 2003, 34 (6): 736–743.
[4] M. Pilch, C. A. Erdman. Use ofbreakup time data and velocity history data to predict the maximum size of stablefragments for acceleration-induced breakup of a liquid drop[J]. InternationalJournal of Multiphase Flow, 1987, 13(6):741-757.
[5] T.-W Lee and Lee, J. Y.,Momentum effects on drop size, calculated using the integral form of theconservation equations[J]. Combust. Sci. Technol., 2012, 184, 434-443.
[6] T.-W Lee and Ryu, J. H.,Analyses of spray break-up mechanisms using the integral form of theconservation equations[J]. Combust. Theory Model., 2014, 18, 89-100.
[7] T.-W Lee and An, K., Quadraticformula for determining the drop size in pressure-atomized sprays with andwithout swirl[J]. Phys. Fluids 28, 2016, 063302.
[8] T.-W Lee, Park, J. E. andKurose, R., Determination of the drop size during atomization of liquid Jets incross flows[J]. At. Sprays 28,2018, 241-254.
[9] T.-W Lee, Park, J. E.,Determination of the Drop Size During Air-Blast Atomization[J]. Journal ofFluids Engineering, 2019, 141(12).
[10]Mayer, E., Theory of LiquidAtomization in High Velocity Gas Streams[J]. ARS Journal, 1961, V31(12):1783-1785.
[11]王军杰.气液同轴剪切喷嘴雾化模型研究[D].北京:北京航空航天大学,2017
[12]L. Qin, R. Yi, L. Yang.Theoretical breakup model in the planar liquid sheets exposed to high-speed gasand droplet size prediction[J]. International Journal of Multiphase Flow, 2018,98: 158-167.
[13]Q. Fu, M. Yao, L. Yang et al.Atomization model of liquid jets exposed to subsonic crossflows[J] AIAAJournal, vol.58, No.5, 2020
[14]K. Ghorbanian, M. Soltani , M.Morad M et al. Neural Network Prediction of a Liquid-Liquid Coaxial SwirlInjector Performance Map[C]// AIAA Aerospace Sciences Meeting & Exhibit.2013.
[15]J. H. Im, S. Cho, Y. Yoon etal. Comparative Study of Spray Characteristics of Gas-Centered andLiquid-Centered Swirl Coaxial Injectors[J]. Journal of Propulsion & Power,2015, 26(6):1196-1204.
[16]王小川. MATLAB神经网络43个案例分析[M]. 北京航空航天大学出版社, 2013.
这篇关于神经网络 mse一直不变_神经网络法预测喷雾液滴尺寸的粗浅尝试的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









