递归 从最简单开始 逐步深化的理解 +举例说明 （n的阶乘、斐波那契数列、n个台阶不同走法、蓝桥杯第39级台阶） C++

先看三个拓展题目：

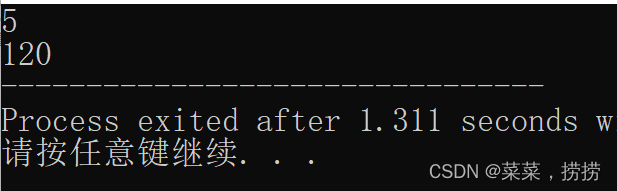
一、求n的阶乘（1<n<1000）?

例如n=5;  5的阶乘：5*4*3*2*1=120

//递归
#include<iostream>
using namespace std;
int fun(int n){if(n==1)return 1;elsereturn n*fun(n-1);
}
int main(){int n;cin>>n;cout<<fun(n);return 0;
}//————————————————————————————————————————————————————————————————————————————————————/*
//非递归
#include<iostream>
using namespace std;
int main(){int n,sum=1;cin>>n;while(n>0)sum*=n--;cout<<sum;return 0;
}
*/

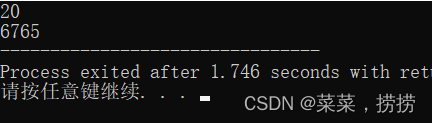
 二、求斐波那契数列的第n项是多少？

斐波那契数列：1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765........

规律：前两个数相加等于后面的第三个数（a[i] = a[i-1] + a[i-2] ,其中i>=3）;

//递归
#include<iostream>
using namespace std;
int fun(int n){if(n==0)return 0;else if(n==1)return 1;else return fun(n-1)+fun(n-2);
}
int main(){int n;cin>>n;cout<<fun(n);return 0;
}//——————————————————————————————————————————————————————————————————————————— /*
//非递归 
#include<iostream>
using namespace std;
int main(){int n;cin>>n;int aa[n+1];aa[1]=aa[2]=1;for(int i=3;i<=n;i++)aa[i]=aa[i-1]+aa[i-2]; cout<<aa[n];return 0;
}
*/

三、楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,编一程序计算共有多少种不同的走法.
设n阶台阶的走法数为f(n)，按照倒推法（从楼梯最上面，倒推过来，从n-1台阶到第n台阶的走法，和从n-2到第n台阶的走法），显然有当 n>2 时，f(n)=f(n-1)+f(n-2)，（特别关键，一定要理解透彻，最好能自己动笔推演一遍才能真正的搞清楚）

输入一个整数n（3<=n<=1000)；

输出一个整数表示共有多少种不同的走法。

#include<iostream>
using namespace std;
int fun(int n){if(1==n)return 1;else if(2==n)return 2;elsereturn fun(n-1)+fun(n-2);
} 
int main(){int n;cin>>n;cout<<fun(n)<<endl;return 0;
}//提示：非递归可用排列组合的方法实现，过程略显复杂，代码省略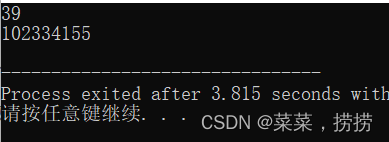

（39阶台阶，102334155）

-------------------------------------------------上主菜 -------------------------------------------------------------

四、第39级台阶
小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!
站在台阶前，他突然又想着一个问题:

如果我每一步 只能迈上1个或2个台阶。先迈左脚，然后左右交替，
最后一步是迈右脚，也就是说共要走偶数步（不同点） 。

那么，上完39级台阶， 有多少种不同的，上法呢?
请你利用计算机的优势，帮助小明寻找答案。

要求提交的是个整数。
注意:不要提交解答过程，或其它的辅助说明文字。

（答案：51167078）

#include<iostream>
using namespace std;
int ans=0; 
void fun(int step,int s){     //step表示还剩余多少步（台阶），s表示走了多少步，if(step<0)return;else if(0==step &&s%2==0)ans++;else{fun(step-1,s+1);fun(step-2,s+1);}	
} 
int main(){fun(39,0);cout<<ans<<endl;return 0;
}//提示：非递归可用排列组合的方法实现，过程略显复杂，代码省略

非递归：运用排列组合的方法

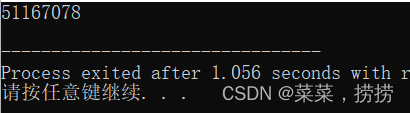
注：102334155 / 2 = 51167077.5 ==> 51167078

总结：

• 由一、二可以看出递归不一定就比非递归简单，其实一、二递归算法的效率远远低于非递归，数据稍微大一点就能明显感觉出来，递归要好几秒甚至十多秒才能出答案，非递归却依然还是一两秒就能出答案；
• 由三、四可以知道：递归对于一些比较复杂问题还是很好用的（要不然怎么说高手都用递归呢），当然，好用基本都只是在于代码量简单了，就是有些废脑子，容易烧坏脑袋；
• 由这四个递归程序（逐渐复杂）可以很好的帮助理解递归的原理，对递归很困惑的小伙伴很有帮助，值得研究；
• ………………+++++…………
• 其他总结，还请有想法的读者能共享出自己的总结经验，大家共同进步。