语谱图（五） Mel_语谱图之MFCC系数（上）

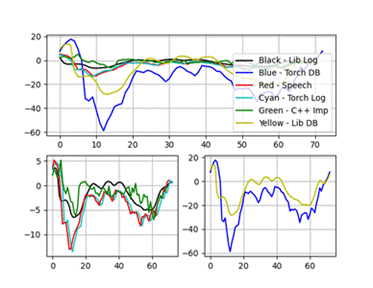
本文主要是介绍语谱图（五） Mel_语谱图之MFCC系数（上），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

搞清语音是怎么产生的对于我们理解语音有很大帮助。人通过声道产生声音，声道的shape（形状？）决定了发出怎样的声音。声道的shape包括舌头，牙齿等。如果我们可以准确的知道这个形状，那么我们就可以对产生的音素phoneme进行准确的描述。声道的形状在语音短时功率谱的包络中显示出来。而MFCCs就是一种准确描述这个包络的一种特征。

也就是说MFCC 最初的出现，是为了描述音频信号短时功率谱的包络，而这个包络中有声道形状的信息在里面；

1.MFCC 定义：

Mel 频率倒谱系数（Mel Frequency Cepstrum Coefficient ）
缩写是MFCC，Mel频率是基于人耳听觉特性提出来的，它与Hz频率成非线性对应关系。

Mel频率倒谱系数(MFCC)则是利用它们之间的这种关系，计算得到的Hz频谱特征

Mel Frequency Cepstrum Coefficient

2.MFCC作用：

和线性预测倒谱系数LPCC一起用于描述语音特征的参数：能量，基音频率，共振峰值等

3.MFCC 生成

3.1 Mel 频率：

是模拟人耳对不同频率语音的感知。

人类对不同频率语音有不同的感知能力：对1kHz以下，与频率成线性关系，对1kHz以上，与频率成对数关系。频率越高，感知能力就越差了。因此，在应用中常常只使用低频MFCC，而丢弃中高频MFCC。

在Mel频域内，人对音调的感知能力为线性关系，如果两段语音的Mel频率差两倍，则人在感知上也差两倍。转换公式：B(f)=1125ln(1＋f/700) 其中f为频率，B为Mel－频率。

3.2 倒谱：

同态处理（指将非线性问题转化为线性问题）的结果，分为复数和实数倒谱，常用实数倒谱，为语音识别中的重要参数。

倒谱：
就是将信号 1.FT傅里叶变换后， 2. 再进行取对数
3. 再进行傅里叶FT 反变换；

倒谱系数提取

具体过程：傅里叶变换----->对数运算----->傅里叶反变换。

语音的产生用源、滤波器模型来表示，即把声带振动看作激励源e(n)，把声道看成一个滤波器h(n)，两者在时域进行卷积，得到语音信号s(n)。为了更好地处理语音，则需要分析s(n)以分别得到e(n)和h(n)，这个过程称为解卷过程。

abs(DFT)、Log、IDFT三步为一个卷积同态信号处理系统，经过这三步之后，倒谱域上

 s\'(n)=e\'(n)＋h\'(n)

激励源和信道已经变成了相加的关系，这时候通过一个倒滤波器，即图中的Cepstral Liftering，就可以把激励源和信道分开了。

3.3 MFCC 提取流程

预滤波：CODEC（所谓Codec，就是编码-解码器“Coder-Decoder”的缩写。说得通俗一点，对于音频就是A/D和D/A转换。）前端带宽为300-3400Hz（语音能量主要集中在250~4500Hz）。的抗混叠滤波器。

工程测量中采样频率不可能无限高也不需要无限高，因为一般只关心一定频率范围内的信号成份。为解决频率混叠，在对模拟信号进行离散化采集前，采用低通滤波器滤除高于1/2采样频率的频率成份。实际仪器设计中，这个低通滤波器的截止频率(fc) 为：

截止频率（fc）= 采样频率（fs） / 2．56

A/D变换：8kHz的采样频率，12bit的线性量化精度。
预加重：通过一个一阶有限激励响应高通滤波器，使信号的频谱变得平坦，不易受到有限字长效应的影响。

将经采样后的数字语音信号s(n)通过一个高通滤波器(high pass filter)： H(z)= 1 – a×z -1 , 0.9 a 1.0 (一般取0.95左右)。经过预加重后的信号为： (n)= s(n)– a×s(n-1)。因为发声过程中声带和嘴唇的效应，使得高频共振峰的振幅低于低频共振峰的振幅，进行预加重的目的就是为了消除声带和嘴唇的效应，来补偿语音信号的高频部分。

分帧：根据语音的短时平稳特性，语音可以以帧为单位进行处理，实验中选取的语音帧长为32ms，帧叠为16ms。

一般取10-20ms为一帧，为了避免窗边界对信号的遗漏，因此对帧做偏移时候，要有帧迭(帧与帧之间需要重叠一部分)。一般取帧长的一半作为帧移，也就是每次位移一帧的二分之一后再取下一帧，这样可以避免帧与帧之间的特性变化太大。

加窗：采用哈明窗对一帧语音加窗，以减小吉布斯效应的影响。

语音在长范围内是不停变动的，没有固定的特性无法做处理，所以将每一帧代入窗函数，窗外的值设定为0，其目的是消除各个帧两端可能会造成的信号不连续性。常用的窗函数有方窗、汉明窗和汉宁窗等，根据窗函数的频域特性，常采用汉明窗。公式是在加窗范围内，w(n)=0.54-0.46cos(2pi*n/(n-1))。

吉布斯现象Gibbs phenomenon（又叫吉布斯效应）：将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。这种现象称为吉布斯现象。

快速傅立叶变换（Fast Fourier Transformation, FFT）：将时域信号变换成为信号的功率谱。

由于语音信号在时域上的变化快速而不稳定，所以通常都将它转换到频域上来观察，此时它的频谱会随着时间作缓慢的变化。所以通常将加窗后的帧经过FFT (Fast Fourier Transform)求出每帧的频谱参数。

三角窗滤波：用一组Mel频标上线性分布的三角窗滤波器（共24个三角窗滤波器，对信号的功率谱滤波，每一个三角窗滤波器覆盖的范围都近似于人耳的一个临界带宽，以此来模拟人耳的掩蔽效应。

将每帧的频谱参数通过一组N个三角形带通滤波器(N一般为20~30个)所组成的梅尔刻度滤波器，将每个频带的输出取对数，求出每一个输出的对数能量(log energy)，k = 1,2,… N。再将此N个参数进行余弦变换(cosine transform)求出L阶的Mel-scale cepstrum参数。